精選版 日本国語大辞典 「群速度」の意味・読み・例文・類語
ぐん‐そくど【群速度】
- 〘 名詞 〙 連続した正弦波によって作られる合成波が伝わる速度。物質中で光は色によって速度が異なるので、各色の光の速度と群速度は一致しない。
最新 地学事典 「群速度」の解説
ぐんそくど
群速度
(1)group velocity
周期,波長を異にする二つの波A=cos〔(p+Δp)t-(ξ十Δξ)x〕とAcos〔(p-Δp)t-(ξ-Δξ)x〕が存在するとき(Δp≪p, Δξ≪ξ),その合成された波は2Acos(pt-ξx)・cos(Δpt-Δξx)となり,うなりの現象を示す。第一の因子(振幅を別にして)が表す波では,振動数,波数はそれぞれ初めの二つの波の平均,第二の因子では差の1/2であり,後者は前者に比べはるかに長周期,長波長となる。前者は搬送波であり,位相の伝わりを表し,その速度はp/ξ(=c)。これに反し,後者は変調波,前者の包絡線,振幅変化の波で,速度はΔp/Δξ(=U)である。その一波の中には多くの搬送波の群を含むので,Uを群速度と称する。cが一定のときU=cである。連続的に振動数,波数が変化する波を合成して得られる∫A(ξ)cos(p(ξ)t-ξx)dξをKelvinの停留値法によって評価するとき,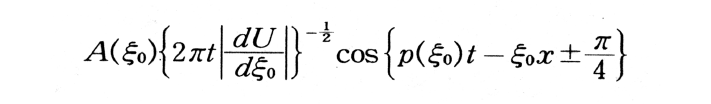
となる。ここでξ0は,t=x/U=x/(dp/dξ)を満たすξの値である。したがって信号は群速度Uで伝わることになる。dU/dξ=0の所では上式は成り立たず,別の近似をしなくてはならない。
執筆者:佐藤 泰夫
(2)group rate
G.G.Simpson(1955)によって提案された進化速度の一つ。ふつう,生物の特定の綱や目のなかの属の平均寿命で示される。R.Pear(1940)は,横軸に地質時代の絶対年数を,縦軸に絶滅属や現生属の百分率を目盛って,これらの点を結んで得られた曲線を生存曲線(survivorship curve)と呼んだ。この曲線から,属の平均生存率(mean survivorship)を求めることができる。Simpson(1944~55)は,106年間に現れる特定の綱や目の属数を,その発現率(rate of origin)といい,消滅するそれを消滅率(rate of disappearance)と呼び,これから平均寿命を求めている。
執筆者:大森 昌衛
参照項目:エアリー相
出典 平凡社「最新 地学事典」最新 地学事典について 情報
改訂新版 世界大百科事典 「群速度」の意味・わかりやすい解説
群速度 (ぐんそくど)
group velocity
波の速度の一つ。波の位相速度は波長(または振動数)によって変化し(波の分散という),例えば,深い水の表面の波の速さは波長1cmで24.7cm/s,波長1mで1.25m/sとなり波長が長いほど速い。さて波長のわずかに異なる二つの波が重なり合うと,ある場所では波の山と山とが重なって振幅が大きくなるが,そこを離れると山の位置がしだいにずれるため重ね合わせた波の振幅は小さくなり,二つの波の山と谷とが重なる場所でもっとも小さくなる。その結果,全体を見ると波の振幅が周期的に変化していて,いわば波のかたまりができているように見える。このような波のかたまりを波束wave packetという。波束は分散がなければその形を変えずに二つの正弦波と同じ速さで進むことは明らかである。しかし,分散があるとそれぞれの正弦波は異なる速さで進むため,波束はそのいずれとも異なる速さで進む。図で二つの正弦波の波長と位相速度をそれぞれλとλ+⊿λおよびvとv+⊿vとしよう。時刻tに二つの正弦波の山p0とp0′が重なる場所が波束の山である。しかしp0とp0′とは別の速さで進むので,時間がたつとずれてしまい,そのかわりにp-1とp-1′とが重なって新しい波束の山となる。p-1′がp-1に追いつくのに要する時間⊿tは図から⊿t=⊿λ/⊿v,その間に波束の山が移動した距離⊿xはv・⊿t-λであるから,その移動の速さvgは,vg=(v・⊿t-λ)/⊿t=v-λ・(⊿v/⊿λ)となる。この波束の移動する速さvgを群速度といい,分散がなければvg=vである。われわれが実際に観測する種々の波は,多くの場合,いくつもの正弦波が重なり合ってできた波束が群速度で進んでいるものを見ているのである。
→位相速度 →波動
執筆者:有山 正孝
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「群速度」の意味・わかりやすい解説
群速度
ぐんそくど
波束が分散性媒質内を伝わる速度。ここに波束というのは、先端から後尾まで有限の長さに広がる一つながりの波のかたまりであり、これは有限の振動数領域にわたる正弦波の重ね合わせとみなすことができる。分散性媒質というのは、その媒質内では正弦波の波面の進行速度(位相速度)が振動数によって異なり、したがって屈折率が振動数によって異なるような媒質である。正弦波の波面が進行する速度(位相速度)vは、v=ν・λ=ν/kである。ここに、νは振動数、λは波長、kは波数すなわち波長の逆数である。群速度vgはvg=dν(k)/dkである。すなわち、波数kの関数としての振動数ν(ν=ν(k))をkで微分した微係数に等しい。位相速度vを波数kの関数としてv=v(k)と書くと、群速度vgは、
vg=v+k・dv(k)/dk
とも書ける。分散性媒質では、群速度vgは、位相速度vと異なる値をもつ。
電子のような物質波においては、物質波の波束が粒子に対応する。粒子のエネルギーE、運動量pと、物質波の振動数ν、波数kの間には、アインシュタイン‐ド・ブローイの関係
E=hν, p=hk
が成立する。ここに、hはプランク定数である。粒子のEとpとの関係E=p2/(2m)(ここにmは粒子の質量)を用いると、
vg=dν/dk=dE/dp=p/m
となる。この結果は粒子の運動量pをその質量で割った商、すなわち粒子の速度が物質波の群速度vgに等しいことを示している。
[飼沼芳郎]
ブリタニカ国際大百科事典 小項目事典 「群速度」の意味・わかりやすい解説
群速度
ぐんそくど
group velocity
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
海の事典 「群速度」の解説
群速度
出典 (財)日本水路協会 海洋情報研究センター海の事典について 情報
世界大百科事典(旧版)内の群速度の言及
【波動】より
…なお,正弦波に限らず位相速度vでx軸方向に進む波は,一般に,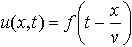 の形で示される。
の形で示される。
[うなりと群速度]
振動数のわずかに異なる二つの正弦波を重ね合わせると,ある場所で,ある瞬間に波の山と山が重なっていても,しだいに山の位置がずれていくので互いに打ち消し合うようになり,その後再び山の位置が近づいて,山の数が一つだけずれたとき再び山と山が重なり合う。その結果,重なり合った波の振幅は周期的に変化し,1秒間の増減の回数は二つの波の振動数の差に等しい。…
※「群速度」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...