精選版 日本国語大辞典 「コリオリの力」の意味・読み・例文・類語
コリオリ の 力(ちから)
改訂新版 世界大百科事典 「コリオリの力」の意味・わかりやすい解説
コリオリの力 (コリオリのちから)
Coriolis' force
物体の運動を記述する座標系が慣性系(運動の第1法則が成り立つ座標系)でない場合に,見かけの力を作用させて運動法則を成り立たせようとする考え方がある。質量mの質点が一定の角速度ωで原点のまわりに半径rの円運動をしている場合--別な表現をすれば,角速度ωで回転運動を続ける座標系(回転座標系)上で質点が静止している場合--を考えると,加速度は円の中心に向かい,その大きさはω2rとなる。
この回転座標系上でも運動法則が成り立っているとすれば,質点は静止しているのだから中心に向かう力と逆向きの大きさの同じ力が作用し,中心に向かう力を打ち消していると考える必要がある。この仮想的な力(慣性力)を遠心力と呼び,円の中心と反対向きでmω2rの大きさを持つことになる。回転座標系上で静止している質点をそれに固定した座標系からみる場合には,見かけの力として遠心力だけを考えればよいが,回転座標系上で運動している質点に対しては,理論上さらにもう一つの見かけの力を考える必要があり,この力を研究したフランスの物理学者G.G.コリオリにちなみコリオリの力と呼んでいる。このように見かけの力として遠心力やコリオリの力を導入すると,回転系を慣性系のように取り扱うことができ非常に便利である。地球上で運動する物体に働くコリオリの力を例に説明していこう。
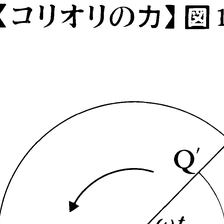
問題を簡単にするために,我々は地球の北極(図1のP点)に立ち,地球と共に回転しているとする。そしてt=0の瞬間にPAの方向に,すなわちある特定の恒星の方向に物体を初速度Vで発射したとする。物体は時刻tにはQに達し,さらにAの方向に飛び続ける。しかしその間に我々の立っている地球は回転しているので北極上に固定した我々の正面はPA′の方向を向くことになる。もしも地球の自転がなかったならば,当然物体がQ′にあるべきものが右方のQにQ′Qだけずれたと考えるにちがいない。このように地球が動かないで物体に何か別な力が働いてその方向を変えたと考えた場合,この見かけ上の力をコリオリの力と呼ぶ。コリオリの力による加速度は2Vωとなる(図1)。
実際の地球はほぼ球であるから,地球の上の任意の緯度φにおけるコリオリの加速度は2Vωsinφとなる(図2)。すなわち,コリオリの力は極ではsinφ=1で最も大きく,赤道ではsinφ=0でゼロになる。地球の自転によるコリオリの力は地球の上を飛ぶあらゆる物体に作用する。例えば大気中に水平方向の気圧傾度があるとき空気はまず気圧傾度の方向に動きだし,しだいに速度を増加する。コリオリの力は速度に比例するので,その影響をしだいに受けるようになり,北半球では右の方へ,南半球では左の方へずれていくことになる。最後には気圧傾度力とコリオリの力はつり合い,空気は等圧線に沿って進むようになる(これを地衡風と呼ぶ)。このような効果は海流の運動にも現れる。なおこのような場合,風や海流の向きを変えるように働くことから,コリオリの力を偏向力または転向力と呼ぶ場合もある。フーコー振子の振動面が回転するのも地球の自転によるコリオリの力を受けるためである。
執筆者:花房 竜男
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「コリオリの力」の意味・わかりやすい解説
コリオリの力
こりおりのちから
回転座標系に見かけのうえで発生する慣性力のこと。たとえば、角速度ωで回転する円板上に、中心から円板の縁に向かって速度vで物体(質量をmとする)を投げると、この物体には進行左側から右側に
f=2mωv
の大きさの力が働く。これは、1828年フランスのコリオリが理論的に導いたので、コリオリの力とよばれる。一般に、回転中心を基準として回転面内の位置ベクトルをrとし、その成分をx、yとすると、コリオリの力fは、回転面に平行で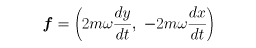
と書ける。
したがって、dr/dtとfの内積をつくると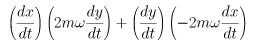
であり、これはゼロになるから、コリオリの力は物体の速度と垂直な方向から働く。コリオリの力はまた回転軸とも垂直になっている。コリオリの力の効果は、広域気象現象、大陸間弾道ミサイルの弾道計算などに重要である。台風が北半球では左巻き、南半球では右巻きになるのも、コリオリの力の影響である。
[大槻義彦]
ブリタニカ国際大百科事典 小項目事典 「コリオリの力」の意味・わかりやすい解説
コリオリの力
コリオリのちから
Coriolis force
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「コリオリの力」の意味・わかりやすい解説
コリオリの力【コリオリのちから】
→関連項目黒潮
出典 株式会社平凡社百科事典マイペディアについて 情報
最新 地学事典 「コリオリの力」の解説
コリオリのちから
コリオリの力
Coriolis’ force
地球が自転しているために慣性力として現れる見かけの力。転向力とも。北半球では風を運動方向に対して直角に右向きに曲げるように作用し,南半球では左向きに曲げるように作用する。地球の自転の角速度をΩ,西から東へ吹く成分をu,南から北へ吹く成分をvとし,f=2Ωsinϕ(ϕはその地点の緯度)をコリオリ係数とすると,コリオリの力はdu/dt=fv,dv/dt=−fuで表される。
執筆者:榧根 勇・田中 博
出典 平凡社「最新 地学事典」最新 地学事典について 情報
パラグライダー用語辞典 「コリオリの力」の解説
コリオリの力
出典 パラグライダー用語辞典について 情報
海の事典 「コリオリの力」の解説
コリオリの力
出典 (財)日本水路協会 海洋情報研究センター海の事典について 情報
世界大百科事典(旧版)内のコリオリの力の言及
【座標】より
… すなわち回転系においては力Fに対し見かけ上の力,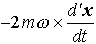 と-mω×(ω×x)とが加わっていることがわかる。回転系でみたときの速度d′x/dtに関係する力
と-mω×(ω×x)とが加わっていることがわかる。回転系でみたときの速度d′x/dtに関係する力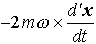 がコリオリの力と呼ばれるものであり,また-mω×(ω×x)は遠心力である。
がコリオリの力と呼ばれるものであり,また-mω×(ω×x)は遠心力である。
[解析力学における一般化座標]
質点の運動を記述するのには,その位置を表す変数と同時に速度または運動量が独立な変数として必要であるが,これは運動方程式が時間に関する2階の常微分方程式であることに起因している。…
※「コリオリの力」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...