改訂新版 世界大百科事典 「スピノル」の意味・わかりやすい解説
スピノル
spinor
電子のように1/2のスピンをもつ状態,さらに一般に任意のスピンをもつ状態を表すために導入された量で,スピノルの名もスピンに由来している。三次元空間を回転させたとき,その中の量は回転に伴って変化するが,その変化のしかたによってスカラー,ベクトル,テンソルなどに区別される。変化しないものをスカラーといい,空間内の変位を表す矢印と同じようにふるまうのがベクトルであり,数個のベクトルの積と同じように変化するのが高階のテンソルである。回転群の表現論によると,空間回転の際の変化のしかたとしては,上記以外のものが存在する。スピノルはベクトルの平方根とでもいうべきもので,2個のスピノルの積がベクトルとなる。ベクトルはその座標成分によって(ax,ay,az)のように3個の実数で表され,回転によりa′=Aaと3行3列の直交行列Aで変換される。これに対しスピノルは2個の複素数(u1,u2)で表され,回転でu′=Uuと2行2列のユニタリ変換をうける。すなわちベクトルが回転群の三次元表現であるのに対して,スピノルは回転群の二次元表現で,uαとその複素共役量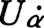 との積のある組合せがベクトルと同様にふるまうことが示される。スピノルは回転群の2価表現である。すなわち,空間を1回転(360度回転)させたとき,ベクトルはもとのものにもどるが,スピノルuは-uとなり,2回転(720度回転)で初めてもとの価にもどる。
との積のある組合せがベクトルと同様にふるまうことが示される。スピノルは回転群の2価表現である。すなわち,空間を1回転(360度回転)させたとき,ベクトルはもとのものにもどるが,スピノルuは-uとなり,2回転(720度回転)で初めてもとの価にもどる。
以上は三次元空間の回転の場合であるが,ベクトル,テンソルが相対論的なローレンツ変換にまで拡張されたように,スピノルも同様に拡張される。ローレンツ変換の場合は,2種類の異なるふるまいをするスピノルが存在し,添字の上つき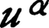 ,下つき
,下つき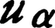 で区別される。反転を含まないローレンツ変換でおのおのが2行2列の行列で変換をうけるが,空間反転の際には下つきが上つきに,上つきが下つきに入れかわる。したがって空間反転で不変な理論では両者を併用しなければならない。電子に対するディラックの相対論的方程式に現れる波動関数は4個の成分をもつが,これは添字の上つき,下つきの2個のスピノルを並べたものであり,これをバイスピノルと呼ぶことがある。数個のスピノルの積からは高階のスピノルがつくられるが,それらは4種の添字,すなわち上つき点なし
で区別される。反転を含まないローレンツ変換でおのおのが2行2列の行列で変換をうけるが,空間反転の際には下つきが上つきに,上つきが下つきに入れかわる。したがって空間反転で不変な理論では両者を併用しなければならない。電子に対するディラックの相対論的方程式に現れる波動関数は4個の成分をもつが,これは添字の上つき,下つきの2個のスピノルを並べたものであり,これをバイスピノルと呼ぶことがある。数個のスピノルの積からは高階のスピノルがつくられるが,それらは4種の添字,すなわち上つき点なし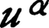 ,上つき点つき
,上つき点つき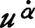 ,下つき点なし
,下つき点なし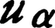 ,下つき点つき
,下つき点つき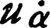 を何個含むかで指定される。偶数個の積はテンソルに帰着され,奇数個の積は2価表現であり,広い意味でのスピノルである。量子力学の言葉でいえば,スカラーはスピンが0の状態であり,スピノルはスピンが1/2,ベクトルはスピンが1の状態で,整数スピンの状態はテンソルで表され,半奇数スピンの状態は2価表現のスピノルで表される。
を何個含むかで指定される。偶数個の積はテンソルに帰着され,奇数個の積は2価表現であり,広い意味でのスピノルである。量子力学の言葉でいえば,スカラーはスピンが0の状態であり,スピノルはスピンが1/2,ベクトルはスピンが1の状態で,整数スピンの状態はテンソルで表され,半奇数スピンの状態は2価表現のスピノルで表される。
執筆者:宮沢 弘成
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「スピノル」の意味・わかりやすい解説
スピノル
spinor
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

