改訂新版 世界大百科事典 「アフィン幾何学」の意味・わかりやすい解説
アフィン幾何学 (アフィンきかがく)
affine geometry
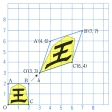
擬似幾何学ともいう。クラインは1872年に有名な《エルランゲン・プログラム》を発表し,その中で幾何学を変換群の立場から統一的に論じ,例えば,図形の性質のうち,合同変換で変わらないような性質を調べるのがユークリッド幾何学であり,射影変換によって変わらない性質を調べるのが射影幾何学であると定義したが,この立場に立つとき,アフィン幾何学とはアフィン変換によって不変な性質を調べる幾何学といえる。この幾何学の源泉はメービウスの《重心算法論Der baryzentrische Kalkül》(1827)にあるが,新しい種類の幾何学として確立したのはクラインである。アフィン変換とは直線をつねに直線にうつし,また線分をつねに線分にうつすような変換を指すが,平行線をつねに平行線にうつす変換といってもよく,この意味で平行変換と呼んでもよいものである。平行移動,回転や折返し(裏返し)などの合同変換はアフィン変換であるが,合同変換でないアフィン変換も無数にたくさんある。例えば,図のようにある1点のまわりの拡大,縮小や,ある1直線のまわりの拡大,縮小は平面上のアフィン変換である。これらの例からもわかるように,アフィン変換では一般に長さ,角の大きさ,面積などの計量的性質は保たれない。しかしながら,2直線が相交わるとか,2直線が平行であるとかなどの線形的性質はアフィン変換で保たれる。したがってアフィン幾何学では,平面や空間のもっている長さなどの計量構造は意味をもたなくなるが,直線,交点などのような線形構造はそのまま残る。平面や空間からその計量構造を捨てて線形構造のみを考えた場合,これらをアフィン平面,アフィン空間という。
アフィン幾何学でも三角形という概念は意味をもつが,ユークリッド幾何学では無数の異なる三角形が存在するのに対し,アフィン幾何学では〈すべての三角形は相等しい〉という定理が成り立つ。平行な直線はアフィン変換で平行な直線にうつるので,アフィン幾何学でも平行四辺形という概念は意味をもち,平行四辺形とそうでない四辺形は等しくならない。台形についても同様である。アフィン変換は平行な線分の比を不変に保つ。したがって,線分の中点,三角形の重心などもアフィン幾何学の対象となり,メネラウスの定理やチェバの定理もこの幾何学の定理となる。アフィン幾何学でもベクトルの概念が定義され,これらの全体はベクトル空間を作る。
平面上に平行座標系をとるとき,アフィン変換は,座標が(x,y)である点を次式で定まる(x′,y′)を座標とする点にうつす写像として解析的に表示される。
x′=ax+by+e,y′=cx+dy+f
ここにa,b,c,d,e,fは定数で,行列式,
は0でないとする。空間のアフィン変換についても同様である。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報