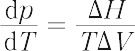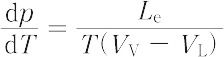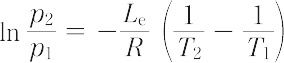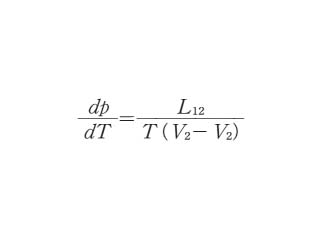クラペイロン-クラウジウスの式（読み）クラペイロンクラウジウスノシキ

化学辞典 第2版

クラペイロン-クラウジウスの式
クラペイロンクラウジウスノシキ
Clapeyron-Clausius equation

蒸気圧と温度の関係を定量的に表す式．B.P.E. Clapeyron(1834年)とR. Clausius(クラウジウス)(1850年)によって導かれた．蒸気圧をp，絶対温度をTとすれば，もっとも一般的な形では，

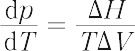
で表される．ここで，ΔHは二つの相(液相と気相，固相と気相)のエンタルピー差，ΔVは同じ量の体積差である．液体を例にとれば，ΔHのかわりに蒸発熱 L_e を用い，同量の液体と気体の体積をそれぞれ V_L，V_V とすれば，

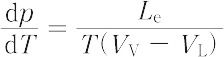
となり，近似的に，L_e は温度に無関係の定数とみなし，かつ蒸気の体積に比して液体の体積を無視し，また蒸気を理想気体とみなして上式を積分すると，二つの温度 T₁，T₂ における蒸気圧 p₁，p₂ の関係は，次式で与えられる．

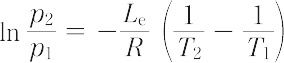
したがって，蒸気圧の対数を1/Tに対してプロットすると直線が得られ，その直線の傾斜は，－ L_e/Rに等しい．同様のことは固体の蒸気圧(昇華圧)に対してもいえる．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

クラペイロン＝クラウジウスの式
クラペイロン＝クラウジウスのしき
Clapeyron-Clausius' equation

沸騰中の湯，氷が浮かんだ水のように，物質の2つの相が圧力 p ，温度 T で熱平衡にあるとし，各相の比体積を v₁，v₂ ，転移熱を L とすれば，単位質量の物質が相1から相2へ相転移するとき，次の式が成り立つ。

dp/dT＝L/T(v₂－v₁)

これをクラペイロン＝クラウジウスの式といい，初め B.クラペイロンが熱素説により，のちに R.クラウジウスが熱力学の法則から導き出した。沸騰の場合には，液体の比体積 v₁ に比べて気体の比体積 v₂ のほうが必ず大きく，v₂－v₁＞0 であるから dp/dT＞0 となり，外圧が増せば沸点が上昇する。融解の場合には，たいていの固体のように融解すると体積が増す物質では固体と液体の比体積 v₁，v₂ の差は v₂－v₁＞0 であるから，圧力が増せば融点が上昇する。これに対し，水や活字合金のように融解すると体積が減る物質では v₂－v₁＜0 であって，圧力が増すと融点が降下する。氷に圧力を加えると接触部が解け，圧力を減らすと復氷するのはこのためである。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

クラペイロン‐クラウジウスの式【Clapeyron-Clausius' equation】

一成分系で二つの相が熱力学的に平衡にあるとき，その平衡圧力を p，絶対温度を T とし，第一相の容積を V₁，第二相の容積を V₂ として，温度 T でこの物質を第一相から第二相へと単位量を可逆的に移すとすると，このときにこの物質が吸収する熱量を L₁₂ とすれば

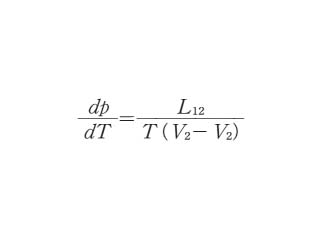
となる．クラウジウス‐クラペイロンの式＊と書くこともある．

出典　朝倉書店