バンド構造（読み）バンドコウゾウ（その他表記）band structure

デジタル大辞泉

バンド‐こうぞう〔‐コウザウ〕【バンド構造】

結晶内の電子のエネルギー準位がとる帯状の構造。エネルギーが低い順から価電子帯、禁制帯、伝導帯が並び、電子はパウリの原理に従ってエネルギー準位が低いところから順に埋まっていく。絶縁体および半導体では、価電子帯と伝導帯の間に電子が存在しない禁制帯がある。導体の場合、価電子帯にフェルミ準位があり、それを上回るエネルギーをもつ電子が電気伝導に寄与する。このようなバンド構造に基づいて、電子がかかわる固体の性質を扱う理論をバンド理論という。帯構造。

出典　小学館

改訂新版　世界大百科事典

バンド構造 (バンドこうぞう)
band structure

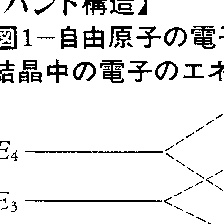
結晶中の電子の量子状態のエネルギー準位の構造。自由な原子や分子では，電子は特定の原子や分子に束縛されていて，そのエネルギー準位は離散的なとびとびの値をとる。しかし多数の原子や分子が集まって結晶をつくると，電子は特定の原子や分子に所属することなく結晶全体を動きまわる波（ブロッホ波）となり，そのエネルギー準位は帯（バンド）状の構造をつくる。例えば，N個の原子が互いに十分遠く離れている場合には，自由原子の電子のエネルギー準位E_nがそれぞれN個ずつ縮退して存在するが，原子間隔が小さくなって互いに近づくと，原子間の相互作用によって縮退がとれて，少しずつ値の異なるエネルギー準位がE_nのまわりに連続的に分布して，一つのエネルギー帯（エネルギーバンドenergy band）をつくる。このようなエネルギー帯の集合（図1）が，結晶中の電子のエネルギー準位の全体を構成しバンド構造をつくる。深いエネルギーをもつ内殻電子は各原子に強く束縛されていてそのエネルギー帯の幅（バンド幅）は狭いが，エネルギー準位が浅くなるにつれて，各原子の電子の軌道は外側に広がり，原子間の相互作用が強くなり，バンド幅は広くなる。さらに浅くなるといくつかのエネルギー帯が互いに重なり合うようになり，電子は結晶中でほとんど自由な電子のようにふるまう。エネルギー帯の間に重なりがなくエネルギー準位の存在しないエネルギー領域がある場合，これを禁止帯forbidden bandという。

　電子はフェルミ粒子であるから，フェルミ分布に従って低いエネルギーから各準位にスピンの異なる2個ずつの電子が満たされていくが，絶対0度では，フェルミ準位（E_f）より低い準位に結晶中の全電子が収容され，それより高い準位は空になっている。一つのエネルギー帯には結晶の単位胞の数Nの2倍の電子が収容されるが，完全に満たされたエネルギー帯（充満帯filled band。価電子帯valence bandともいう）は電流を流すことはできない。したがって，フェルミ準位が禁止帯にあって，充満帯と完全に空のエネルギー帯（伝導帯conduction band。この場合とくに空帯ともいう）がエネルギーギャップ（禁止帯の幅のことでバンドギャップともいう）によって隔てられている場合（図2-a），熱的にあるいは光の吸収などによって充満帯の電子が上の空帯に励起されないかぎり電流は流れないので絶縁体（エネルギーギャップが小さい場合は半導体）になる。しかし，フェルミ準位がエネルギー帯（伝導帯）の中にある場合（図2-b）には，電子は任意の電場によってより高いエネルギー準位に連続的に加速されて電流を生ずるので導体（金属）になる。なおバンドモデルが成り立つかぎり，単位胞中の電子数が奇数の固体は必ず金属になる。

　量子力学的には結晶中の電子は波動である。運動量pをもつ自由電子は波数kの平面波e^ik˙^rで表され（rは位置ベクトル），p＝ħkであるが（ħはプランク定数を2πで割ったもの），結晶中の電子は，平面波が結晶格子と同じ周期性をもつ周期関数u_k（r）で変調されたブロッホ波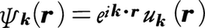，になっており，格子ベクトルRに対して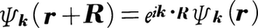，が成り立つ（ブロッホの定理）ので，ħkは結晶運動量と呼ばれる。このように，各エネルギー帯の連続的なエネルギー準位は波数kで指定され，エネルギー帯の指標をnとしてE_n（k）と書ける。E_n（k）を波数kの関数とみるとき，結晶が格子ベクトルの周期性をもつことに対応して，E_n（k）には逆格子ベクトルGの周期性があり（E_n（k＋G）＝E_n（k）），また結晶に回転αの対称性があると，E_n（k）にも回転αの対称性がある（E_n（αk）E_n（k））。

　バンド構造E_n（k）は，通常，第1ブリュアン帯と呼ばれる逆格子空間の単位胞の中で表示される。例えば面心立方格子の第1ブリュアン帯は図3のごとくであるが，立方対称がある場合は1/48の領域でE_n（k）を表示すれば十分である。例として，シリコンの価電子（3s，3p軌道）に由来するエネルギー帯を図4に示してあるが，Γ，X，L，Kなどの記号は図3のk空間の点に対応している。フェルミ準位は灰色で示した禁止帯にあるので，それより下が充満帯（価電子帯），上が空の伝導体で，エネルギーギャップが約1.1eVの半導体であることがわかる。結晶中の波数kの電子は，群速度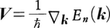，で運動するが，一様な電場Eと磁場Bが外部から作用すると，電子の速度は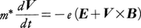，に従って変化する（eは電気素量）。m^＊はE_n（k）曲線の曲率から決まる有効質量で，m^＊＜0の場合には，電子は力を受ける方向と逆向きに加速されるので，正電荷eをもつ質量｜m^＊｜の正孔と解釈される。図4の価電子帯の頂上Γ₂₅付近が正孔である。

　金属の場合には，フェルミ準位E_fがエネルギー帯の中にあるので，E_n（k）＝E_fで決まるk空間における等エネルギー面をフェルミ面という。例として，銅のフェルミ面を第1ブリュアン帯の中で描いたものを図5に示す。フェルミ面の内部の準位はすべて電子で満たされており，外部はすべて空である。したがって，フェルミ面上の電子は，ごくわずかのエネルギーによってでもフェルミ面の外部の状態に励起されるから，金属は任意の電場によって電流が流れるし，ごく低温でも電子は比熱に寄与することができる。そのほか金属の多くの性質が，フェルミ面およびその付近のバンド構造によって決まっている。

　このように，固体の電子構造はエネルギー帯の概念によってうまく整理され，個々の固体のいろいろな性質を理解する基礎を与える。最近では，電子計算機を使っていろいろな固体のバンド構造を正確に計算できるようになり，固体のバンド構造を知ることは，固体物理の研究に欠くことのできないものになっている。
執筆者：浅野 摂郎

図1～図5

出典　株式会社平凡社「改訂新版　世界大百科事典」