回転体（読み）カイテンタイ（英語表記）solid of revolution

デジタル大辞泉

かいてん‐たい〔クワイテン‐〕【回転体】

平面図形を、同一平面上の一つの直線のまわりに1回転させたときにできる立体。球・直円柱・直円錐など。

出典　小学館

精選版 日本国語大辞典

かいてん‐たいクヮイテン‥【回転体】

1. 〘 名詞 〙 空間内の平面上の図形を、その平面上にある一直線のまわりに一回転させてできる立体の総称。
   1. [初出の実例]「円すいは直線を廻転して作られ、球は円を廻転して作られた図形であり、両方とも廻転体である」(出典：生活単元学習の批判（1953）〈遠山啓〉二)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

回転体 (かいてんたい)
solid of revolution

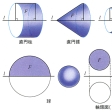
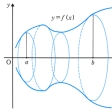
1平面上の曲線cを，その平面上の直線lのまわりに回転したときに生ずる曲面を回転面といい，このときできる立体を回転体という。cを母線，lを回転軸といい，回転面をlを含む半平面で切った切口を子午線という。円，二等辺三角形，長方形をそれらの対称軸のまわりに回転したときに生ずる球，直円錐，直円柱は回転体で，その表面は回転面である。円をそれと交わらない直線のまわりに回転したときに生ずるトーラスもそうである。ろくろを用いて作られた各種の工作物は回転体の形状をしている。区間［a，b］で定義された連続関数y＝f（x）がつねに負でないとき，これをx軸のまわりに回転したときの回転体の体積Vおよび回転面の表面積Sは，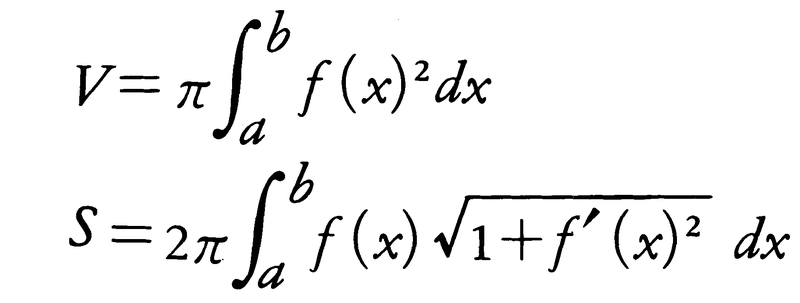

で与えられる。
→パップス=ギュルダンの定理
執筆者：中岡 稔

図－回転体

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

回転体
かいてんたい

平面内の図形Fをこの平面内の直線lの周りに1回転させたときのFの軌跡を回転体といい、lを回転軸という。とくにFが曲線のとき、回転体を回転面といい、Fを母線(ぼせん)という（図A）。このとき、回転中のFの任意の位置を子午線ということもある。回転体の表面は回転面である。Fが曲線y＝f(x)と2直線x＝a、x＝bとx軸によって囲まれる図形のとき、x軸の周りの回転体の体積Vは定積分

で与えられる（図B）。

［高木亮一］

回転体〔図A〕

回転体の体積〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

回転体【かいてんたい】

平面上の図形をその平面上の一直線を軸として一回転したときできる図形。特にもとの図形が曲（直）線のときできる図形を回転面という。球，直円錐などは回転体。円錐曲線を軸のまわりに回転すれば回転楕円面，回転放物面，回転双曲面（一葉と二葉）ができる。
→関連項目球｜パップス=ギュルダンの定理

出典　株式会社平凡社