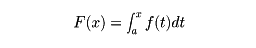改訂新版 世界大百科事典 「実関数論」の意味・わかりやすい解説
実関数論 (じつかんすうろん)
theory of real functions
微積分学およびそこから発展して実変数の関数について論ずる解析学の主要な分野の一つである。17世紀後半にI.ニュートン,G.W.F.ライプニッツによって発見された微分積分法は,19世紀前半に至ってA.L.コーシーによって一応の体系が整えられた。すなわち,彼は極限の概念を定式化することにより解析学の基礎を築いた。コーシーの2著書(1821,23)では,当時までの不完全な理論と比べれば著しい厳密さで微積分学を展開している。しかしその理論は,現在の立場から見れば,部分的にはなお不十分な個所も多かった。19世紀の中期に至り,微積分学は,その基礎的諸概念を確立し精密にするという方向に発展した。これが実変数関数論,すなわち実関数論の起りということができる。
関数の概念は解析学の基礎をなすものであるが,この概念はコーシー以前には直観的に漠然ととらえられていて,例えば,〈変数と定数とから組み立てられた式〉というような定義が通用していた。コーシーは関数の概念を一応は一般的に定義したが,彼はまだ,式によって定義される関数という観念に,暗にとらわれていたようである。19世紀の中期になって,P.G.L.ディリクレが関数を数から数への対応として定義したことにより,一般の関数の概念が初めて確立された。また,コーシーの時代には極限の概念は確立していても一様収束の概念がなかったため,いくつかの誤った結果が導かれたが,N.H.アーベルによる一様収束の概念の発見によってそれらの問題点が明確になり,誤りは正された。続いてG.F.B.リーマンは,積分の定義を反省してそれを一般にした論文を発表し(1854),さらにG.カントルは無理数論ならびに集合論を創始した(1872)。
これよりさき,J.B.J.フーリエは熱伝導に関する有名な論文(1812)を書き,すべての関数はいわゆるフーリエ級数で表されることを論じたが,これが解析学に及ぼした影響は大きい。すなわち,ディリクレが関数の現代的な定義を確立したのは彼のフーリエ級数に関する二つの論文(1829,37)においてであり,また,アーベルの一様収束概念の発見,リーマンによる積分の一般的な定義,カントルの無理数論,集合論の創始も,フーリエ級数が一つの誘因であったと思われる。
リーマンは現在のいわゆるリーマン積分の基礎を築いたが,19世紀の後半に至って微積分学の方法がさらに反省され,極限演算の場としての実数の概念をいっそう明確にすることが必要となって,無理数論が生まれた。J.W.R.デデキントとカントルの論文(いずれも1872),K.ワイヤーシュトラスのベルリン大学における講義は,互いに独立に無理数の理論を創設したものであるが,それらは互いに同値な理論である。無理数論の確立により,微積分学は初めて現代の厳密さに到達できたといえる。無理数についてのカントルの論文は,実数論の基礎を与えると同時に集合論の発端ともなった。集合論は,数学において本質的な役割を演ずる無限の概念を解明し,また数学のあらゆる分野の基礎となった。微積分学も集合論の基礎のうえに立って近代化され,現代の実関数論にまで深められたのである。
実関数論において中心的役割を果たすのは,20世紀の初めにH.ルベーグの画期的な学位論文(1902)によって創始された測度と積分の理論である。彼は直線上の図形の長さ,平面図形の面積,空間図形の体積の概念を,できるだけ一般な図形の範囲に拡張することを考え,測度という概念を導入し,それをもとにして積分の理論を展開した。この測度が彼の名を冠して呼ばれるルベーグ測度であり,ルベーグ測度をもとにして構成される積分がルベーグ積分である。ルベーグ積分はリーマン積分の拡張であるばかりでなく,リーマン積分と比べて多くの利点がある。例えば,積分と他の種々の極限演算(微分演算,関数列の極限をとること,関数を項とする無限級数の和を作ることなど)との順序の交換や,二重積分の順序の交換などが,非常に一般的な条件のもとで可能である。このような便利さのために,ルベーグ積分の効用は解析学の諸分野に及び,例えばフーリエ級数・フーリエ解析の理論はルベーグ積分を活用することによって,初めて満足すべき結果が導かれるのである。
ルベーグの測度の概念の発見と,それによる積分論によって,実関数論はそれ自体として発展を続けるとともに,20世紀全般を通じて,解析学の他の種々な部門に対しても,有力な方法を提供してきた。とくに,フーリエ解析の理論は,関数解析学の発展とあいまって,いろいろな形の関数空間の場合に拡張されて発展しつつある。
→解析学 →関数解析学 →微積分学
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報