改訂新版 世界大百科事典 「フーリエ解析」の意味・わかりやすい解説
フーリエ解析 (フーリエかいせき)
Fourier analysis
フーリエ級数,フーリエ変換(ふーりえへんかん)などを用いて関数の性質を研究し,種々の応用を論ずる分野をフーリエ解析という。実験によって数値的に与えられた関数のフーリエ級数を求める方法は調和解析といわれる。相異なる周期の調和振動の和は必ずしも周期関数でないので,一般に関数の値からこのかくれた周期を見つけることを周期解析という。これらもフーリエ解析の分野である。
(-∞,∞)上で可積分な関数fに対して,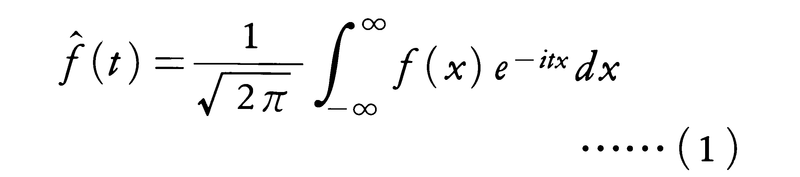
はtの連続関数である。このf^をfのフーリエ変換という。fが(-∞,∞)上で2乗可積分ならば,任意のa>0に対して,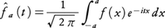 が定義され,
が定義され,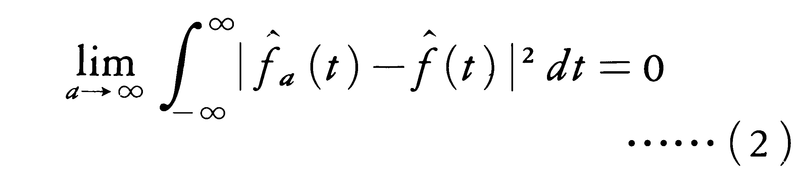
となる関数f^(t)が存在し,(-∞,∞)上で2乗可積分で,このf^をfのフーリエ変換という。一般に(2)が成立するとき,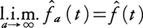 と書いてf^aはf^に平均収束するという(記号l.i.m. はlimit in meanと読む)。またこのとき,もとの関数fがf^を使って,
と書いてf^aはf^に平均収束するという(記号l.i.m. はlimit in meanと読む)。またこのとき,もとの関数fがf^を使って,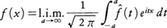 と表され(プランシュレルの定理),パーセバルの等式,
と表され(プランシュレルの定理),パーセバルの等式,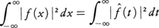 が成立する。fが有限区間(-π,π)上で2乗可積分な関数のとき,上の事実に対応して次のことがいえる。
が成立する。fが有限区間(-π,π)上で2乗可積分な関数のとき,上の事実に対応して次のことがいえる。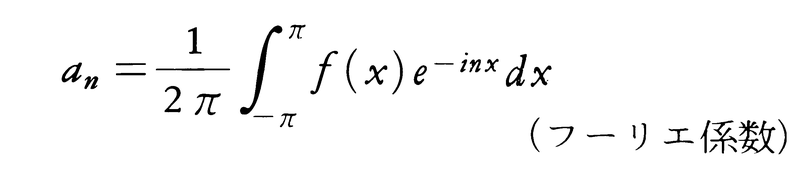
とおくと,フーリエ級数の部分和,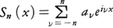 はもとの関数fに平均収束し,パーセバルの等式,
はもとの関数fに平均収束し,パーセバルの等式,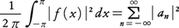 が成立する。また,
が成立する。また,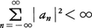 なる任意の数列{an}に対して,
なる任意の数列{an}に対して, はある2乗可積分な関数fに平均収束してパーセバルの等式が成立する。
はある2乗可積分な関数fに平均収束してパーセバルの等式が成立する。
(-∞,∞)上の連続関数fがあって,任意の有限個の実数t1,t2,……,tnと複素数α1,α2,……,αnに対して,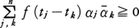 となるとき,fを正の定符号関数または正型関数という。任意の正の定符号関数fに対して,(-∞,∞)上の単調増加右連続関数σ(λ)でα(-∞)=0なるものがただ一つ定まって,
となるとき,fを正の定符号関数または正型関数という。任意の正の定符号関数fに対して,(-∞,∞)上の単調増加右連続関数σ(λ)でα(-∞)=0なるものがただ一つ定まって,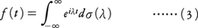
が成立する(ボホナーの定理)。逆に(3)で表される関数fは正の定符号関数である。この事実に対応する数列の場合の結果は次のとおりである。数列{an|-∞<n<∞}において,任意のnと任意の複素数α1,α2,……,αnに対して,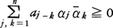 となるとき,{an}を正の定符号数列または正型数列という。正の定符号数列{an}は,[-π,π]上の単調増加右連続関数σ(λ)でσ(-π)=0なるものにより,
となるとき,{an}を正の定符号数列または正型数列という。正の定符号数列{an}は,[-π,π]上の単調増加右連続関数σ(λ)でσ(-π)=0なるものにより,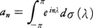 と一意的に表される(ヘルグロッツの定理)。逆にこの式で与えられる数列{an}は正の定符号数列である。
と一意的に表される(ヘルグロッツの定理)。逆にこの式で与えられる数列{an}は正の定符号数列である。
σ(λ)が(-∞,∞)上で有界変動かつ右連続な複素数値関数のとき,(3)と同形式,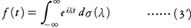
は,f(t)を調和振動eiλtの重ね合せとして表したものと考えられる。逆に,f(t)を与えて,それの固有振動成分の振幅σ(λ)-σ(λ-0)を求めるのが調和解析の問題である。これに関して次の定理が成立する。
(1)f(t)が(3′)の形に表されるためには,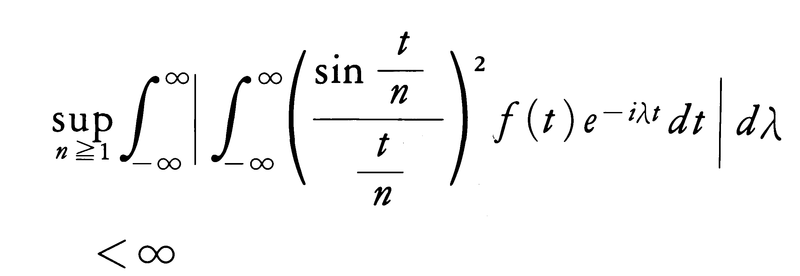
となることが必要かつ十分である。
(2)(3′)のfに対し,任意のλ0において,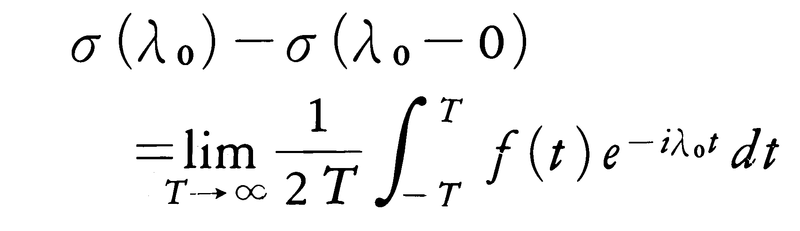
とくにσ(λ)がλ=λ0-δおよびλ=λ0+δ(δ>0)において連続ならば,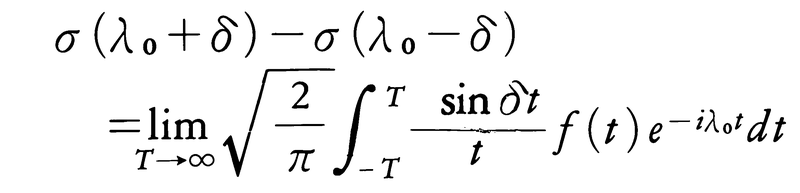
(3)(3′)において有界変動関数σ(λ)の不連続点をλ1,λ2,……とし,σn=σ(λn)-σ(λn-0)(n=1,2,……)とすると,
フーリエ解析はN.ウィーナーによってタウバー型定理にも応用された。タウバー型定理とは,べき級数に関するアーベルの定理の逆に当たるもので,収束半径が1のべき級数Σanznにおいて,an=0(1/n)であって,
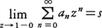 が存在するならば,
が存在するならば,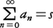 となるという定理である。ウィーナーは次の定理(ウィーナーの一般タウバー型定理という)を示し,それから上記の本来のタウバー型定理を導いた。
となるという定理である。ウィーナーは次の定理(ウィーナーの一般タウバー型定理という)を示し,それから上記の本来のタウバー型定理を導いた。
(-∞,∞)で有界な関数p(x)と定数cがあって,(-∞,∞)上で可積分でそのフーリエ変換f^(t)がすべての実数tで0にならないような一つの関数fに対して,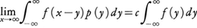 となるならば,(-∞,∞)上で可積分な任意の関数gに対して,
となるならば,(-∞,∞)上で可積分な任意の関数gに対して,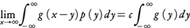 が成立する。
が成立する。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
最新 地学事典 「フーリエ解析」の解説
フーリエかいせき
フーリエ解析
Fourier analysis
結晶中の核外電子密度分布関数は,異常散乱の影響が無視できるときには結晶構造因子を係数とするフーリエ級数に展開される。したがって結晶構造因子の大きさを測定し,位相をなんらかの方法により決定すれば,電子密度が求まり結晶構造が決定できる。j番目の原子の原子散乱因子をfj, 座標を(xj, yj, zj)とすると結晶構造因子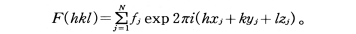
ただしNは単位格子中の原子数。結晶が対称中心をもつときは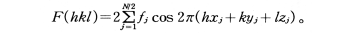
電子密度分布関数ρ(xyz)=1/V・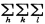 F(hkl)exp{-2πi(hx+ky+lz)},対称中心が存在するときはρ(xyz)=2/V・
F(hkl)exp{-2πi(hx+ky+lz)},対称中心が存在するときはρ(xyz)=2/V・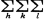 F(hkl)cos2π(hx+ky+lz)。対称が高いときはさらに式が変形できる。各空間群に対するρ(xyz)の式が『Intern.Tables for X-ray Crystallogr.,Vol.Ⅰ』(1967)または,vol.A(1987)に与えられている。
F(hkl)cos2π(hx+ky+lz)。対称が高いときはさらに式が変形できる。各空間群に対するρ(xyz)の式が『Intern.Tables for X-ray Crystallogr.,Vol.Ⅰ』(1967)または,vol.A(1987)に与えられている。
執筆者:丸茂 文幸
出典 平凡社「最新 地学事典」最新 地学事典について 情報
世界大百科事典(旧版)内のフーリエ解析の言及
【正弦波】より
…一般の複雑な波形をもつ波は,周期,波長の異なる多くの正弦波を重ね合わせて合成することができる。任意の波形の波を正弦波に分解する方法はフーリエ解析と呼ばれ,波動現象の理論に多く用いられる。波動【有山 正孝】。…
※「フーリエ解析」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

