期待値（読み）キタイチ（その他表記）expected value
expectation

デジタル大辞泉

きたい‐ち【期待値】

１ A₁,A₂,…,A_nの起こる確率がp₁,p₂,…,p_nであり、それらが起こった場合にx₁,x₂,…,x_nの値をとるとき、x₁p₁＋x₂p₂＋…＋x_np_nの値をいう。例えば、くじ引きで、1本のくじに期待しうる賞金の平均化した値。
２ 《1から転じて》物事に対する期待の度合い。「次の政権に対する期待値が高い」
[類語]伸び代・ゆとり・余地・余裕・期待料

出典　小学館

精選版 日本国語大辞典

きたい‐ち【期待値】

1. 〘 名詞 〙 平均値の一種。確率変数Ｘが、値ｘ、ｙ、…をそれぞれ確率ｐ、ｑ、…でとるとき、Ｘに対して px+qy+… の値をいう。期望値。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

期待値 (きたいち)
expected value
expectation

偶然に支配されていろいろな値をとる変数Xがあるとき，それが平均してどの程度の値をとるかを示す量で，Xの平均値とも呼ばれ，E（X）とかく。例えば1万本のくじの中で，当りくじは，賞金10万円の1等が5本，1万円の2等が20本，1000円の3等が300本で残りはからくじであるとする。このとき1本のくじを引く人は，どれだけの金額を期待するのが妥当であろうかを次のように考える。賞金の総計は100000×5＋10000×20＋1000×300＝1000000円であり，総計1万本のくじがあるのだから1本当り平均100円が期待できる。これを，1，2，3等が当たる確率5/10000，2/1000，3/100とそれぞれの賞金との積の総和と考えて期待値とする。一般に，Xのとる値がx₁，x₂，……で，その値をとる確率がそれぞれp₁，p₂，……のとき，x₁p₁＋x₂p₂＋……＝E（X）として期待値を求めることができる。Xが連続的な値をとるときは，その分布の密度関数をp（x）とかくと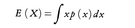，である。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

期待値
きたいち

確率現象の結果が数値で表されている場合、1回の試行の結果期待される数値の大きさを期待値という。たとえば、10000枚のくじのうち、1等10万円、2等1万円、3等1000円の当りくじがそれぞれ2枚、10枚、100枚含まれている。このくじを1枚引いた人はどれだけの金額が期待されるかを考えてみる。1等、2等、3等に当たるのはそれぞれ2/10⁴、10/10⁴、10²/10⁴の割合であるから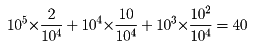

すなわち、40円が期待される金額と考えることができる。実際に受け取るのは10万円か1万円か1000円かまたは0円の四つの場合だけであって、40円受け取るということは現実にはありえない。ここで期待される金額が40円というのは、このくじを引くことを多数回繰り返すとすると、1回当りの平均（相加平均）が約40円であることを意味している。

　一般に確率変数Xがa₁, a₂,……, a_kという値をそれぞれp₁, p₂,……, p_k(p₁＋p₂＋……＋p_k＝1)という確率でとるものとする（前記のくじの場合はk＝4で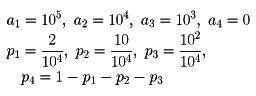

である）。このときXの期待値はa₁p₁＋……＋a_kp_kと定義する。すなわち確率変数の平均値のことを期待値ということもある。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

期待値
きたいち
expectation

いまここに 100本のくじがあり，1等が2本で賞金は 1000円，2等が 10本で賞金は 500円，3等が 30本で賞金は 100円，空くじが残りの 58本とする。このとき，くじ1本あたりの平均の賞金額は，
1/100 (1000×2＋500× 10＋100× 30＋0× 58)
＝1000×2/100＋500× 10/100＋100× 30/100＋0× 58/100＝100
となる。この 100円を，このくじを1本引くときの期待値という。ここで2/100，10/100，30/100，58/100は，1本のくじを引くときの，1等，2等，3等，等外であるためのそれぞれの確率である。一般に，n 個の排反事象 A₁，A₂，…，A_n が起れば，変量 X がそれぞれ x₁，x₂，…，x_n という値をとり，また X が x₁，x₂，…，x_n の値をとる確率がそれぞれ p₁，p₂，…，p_n であるとき，x₁p₁＋x₂p₂＋…＋x_np_n を変量 X の期待値または平均という。ここで p₁＋p₂＋…＋p_n＝1 である。

期待値
きたいち
expectation value

量子力学において，ある波動関数で表わされる状態における物理量を観測したときの測定値として期待される値をいい，波動関数の2乗を確率密度関数としてその物理量の期待値を求める。このとき物理量を1つの演算子とみなす。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

期待値【きたいち】

期望値とも。n個の値x₁，x₂，…，x(/n)が実現する確率がp₁，p₂，…，p(/n)のとき，x₁p₁＋x₂p₂＋…＋x(/n)p(/n)をいう。たとえば100本のくじの中に100円，50円，10円の当りくじがそれぞれ１，２，５本含まれていれば，期待値は（100＋50×２＋10×５）÷100＝2.5円。多数回の測定値の平均は期待値に近い。

出典　株式会社平凡社

世界大百科事典（旧版）内の期待値の言及

【確率】より

…そのため一つの数値で分布の特性量を表すことができれば好つごうである。重要な特性量としては，平均値(期待値ともいう)と分散がある。離散形の場合なら平均値mは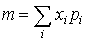，　で，分散σ²は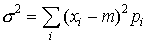，　で与えられる。…

※「期待値」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」