日本大百科全書(ニッポニカ) 「状態和」の意味・わかりやすい解説
状態和
じょうたいわ
多数の粒子からなる体系(物体)に温度や圧力などの外的な条件を課して熱平衡になっているとき、体系の微視的状態にこの条件に適合するような重みをつけて、その和をとった統計量を状態和という。状態和を求めることができれば、体系の熱平衡での状態方程式や熱力学的な性質をすべて導くことができる。熱統計力学でもっとも重要な量である。
多数の分子や原子から構成された体系を特徴づける温度、圧力または体積などの量を熱力学状態変数とよぶ。この状態変数が時間変化しないとき、体系は熱平衡状態にあるという。しかし、原子的な尺度(微視的見地)からみれば、その体系が同じ微視的状態にとどまっているわけではない。たとえば、温度が一定に保たれた容器内の熱平衡の気体でも、その分子は激しく運動しており、各分子の位置や速度も刻々変化していることはよく知られている。つまり、状態変数のような巨視的状態は定まっているが、微視的状態は刻々と変化している。
多数の粒子を含む体系の熱平衡状態は、初期条件に左右されない長時間の平均を求める必要があるが、それを理論的に求めることは非常に困難である。そこで、ギブスは体系の長時間平均をとるかわりに、熱平衡では、この外的条件を満たすような種々な微視的状態がある確率で現れると仮定した。このような重みをつけた微視的状態の集まりを集合(アンサンブル)とよび、熱平衡状態はこのような集合で置き換えることができると考えた。つまり、長時間平均のかわりに適切な集合平均をとればよいことになる。
古典的な系では、微視的状態とは、すべての分子の位置と速度が指定されていることである。そのなかの一つでも異なるときは、別の微視的状態となる。しかし、これらの量は連続値であり、それを測るための枡(ます)(単位)を用意して、それを数えることによって状態数とする。
ここでは、気体を例にとって、微視的状態数の数え方を説明する。一般性を高めるために、微視的状態を指定する速度のかわりに運動量を用いる。解析力学で使われる正準座標qと正準運動量pを用いて微視的状態を指定するのが都合がよい。N個の粒子からなる気体では、各粒子の位置の3成分(qx、qy、qz)とその運動量の3成分(px、py、pz)、まとめて6N個の変数で微視的状態を指定することになる。この6N次元空間のことをΓ(ガンマ)空間または位相空間という。この空間の1点が一つの微視的状態に対応している。変数q、pはすべて連続である。その体積の単位の大きさとして各自由度当り
dqi・dpi=h
(i=1, 2,……, 3N)
とする。ここで、hはプランクの定数である。これは量子論の不確定性原理と関係がある。6N次元のΓ空間ではh3Nを枡として、その体積を数えることになる。つまり、微視的状態数Wは外的条件で許されたΓ空間の体積をΔΓとして
W=ΔΓ/h3N (1)
とすれば、量子論で求める状態数(無次元量)と適合することが知られている。
量子論では体系の微視的状態は、エネルギー定常状態で表され、それを指定する量子数が不連続であれば、条件にあった定常状態に重みをつけてこの集合に取り込めばよい。それでは、外的条件にあった微視的状態の重みをどのように選ぶか。外的な条件によって三つに分けて考える。
[小野昱郎]
孤立系での状態和
いま注目している体系が断熱容器内にあり、外部とは仕事の出入りがないとき、孤立系という。この系の内部エネルギーEと体積Vは一定である。この条件を満たす微視的状態は多数存在し、これがすべて同じ確率で出現するとしよう。このようなエネルギーの等しい微視的状態を同じ重みで集めた集合を小正準集合(ミクロカノニカル・アンサンブル)という。孤立系では、全エネルギーがEからE+dEの微小範囲にあり、体積一定の条件での許される位相空間の体積をΔΓとして、(1)式から決まる微視的状態数を状態和W(E,V)という。
量子系では系の微視的状態はエネルギー定常状態で表される。したがって、許される状態はこの条件を満たす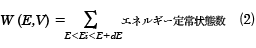
となる。ここで、Eiは定常状態iのエネルギーである。
古典系では、微視的状態は各分子の位置q(q1, q2,……, q3N)と運動量p(p1, p2,……, p3N)によって決まり、その系のエネルギーも各粒子の運動量pと位置qを用いてE(q, p)と表せば、状態和は和のかわり位相空間の積分で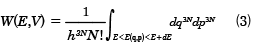
で与えられる。ここで、
dq3N=dq1dq2……dq3N
dp3N=dp1dp2……dp3N
である。(1)式と同様、h3Nで割る必要がある。さらに、全体をN!で割っているのは、N個の同種の粒子からなる場合は、量子論によれば、粒子を交換した微視的状態は同一であるからである。
W(E, V)が求められたとき、その体系のエントロピーSはWを用いて
S(E, V)=klogW(E,V) (4)
のようにEと体積のVの関数として与えられる。ここで、kはボルツマン定数、logはe=2.718……を底とした自然対数を表している。この系の熱平衡温度を絶対温度Tで表すと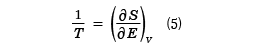
のようにEの関数として与えられる。この式は逆に、温度Tを与えたときの内部エネルギーEの値を決める式でもある。この式で( )VはVを一定としたEでの偏微分を表す。また圧力は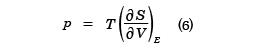
で与えられる。
この式で(5)式を用い、Eを消去すれば、p、V、Tの関係式が得られ、状態方程式である。
[小野昱郎]
定温定積の状態和
もし体系が熱容量の大きな一定温度Tの外界(熱源)に囲まれており、外界と熱の出入り可能のときは、系のエネルギーは一定ではなく、揺らぐことになる。温度Tと体積Vが一定としたときの状態和Z(T, V)は量子系では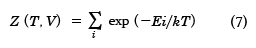
で定義される。ここで、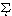 はすべての微視的状態の和をとることを意味している。Eiは微視的状態(エネルギー定常状態)iのエネルギーである。exp(-Ei/kT)をボルツマン因子といい、状態iの重み(出現確率に比例)である。とりうるエネルギーに制限はないが、エネルギーが高いほど出現確率が低いことになる。このような集合を正準集合(カノニカル・アンサンブル)とよぶ。このZを分配関数ともいう。Zは温度Tと体積Vの関数であり、統計力学では重要な量である。
はすべての微視的状態の和をとることを意味している。Eiは微視的状態(エネルギー定常状態)iのエネルギーである。exp(-Ei/kT)をボルツマン因子といい、状態iの重み(出現確率に比例)である。とりうるエネルギーに制限はないが、エネルギーが高いほど出現確率が低いことになる。このような集合を正準集合(カノニカル・アンサンブル)とよぶ。このZを分配関数ともいう。Zは温度Tと体積Vの関数であり、統計力学では重要な量である。
一方、古典系では、エネルギーEは各粒子の運動エネルギーと位置のエネルギーの和であるから、3N次元の運動量pと位置qで表され、状態和は以下のようにΓ空間での積分で表される。
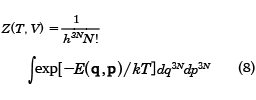
状態和Zが求められると、この系のヘルムホルツ自由エネルギーFは次式で与えられる。
F(T,V)=-kTlogZ(T,V) (9)
ここで、logは自然対数を表す。熱力学の関係式を用いると、Fから圧力pは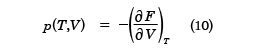
と求められる。pはTとVの関数で表されており、これは状態方程式となる。これは(6)式と同等な式を与える。また、エントロピーSも、TとVの関数として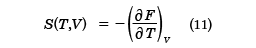
で求められる。この二つの関係式で、この系の熱力学的性質はすべて導くことができる。
[小野昱郎]
理想気体の状態和
理想気体は気体分子間の相互作用を無視し、さらに分子の大きさも無視した極限である。現実の気体でも希薄にすれば、理想気体に近くなる。この場合、古典系での分配関数は厳密に求めることができる。気体の分子並進運動による全エネルギーは運動量のみで表され、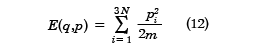
となる。これを用いて、(8)式を積分すれば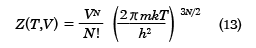
となる。ここで、mは分子の質量である。また、自由エネルギーFは(9)式を用いて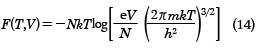
となる。ここで、e(=2.718…)は自然対数の底である。
この式から(10)式を用いてVで偏微分すれば、よく知られた理想気体のボイル‐シャルルの状態方程式
p=NkT/V (15)
が得られる。また、エントロピーは同様に(11)式を用いて、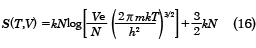
が得られる。この式をザッカー‐テトロードの式という。さらに、定積熱容量CVは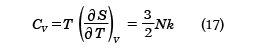
となり、温度に依存しない一定の値となる。実在の単原子分子気体では十分高い温度ではこの値であることが、実験でも確かめられている。また内部エネルギーは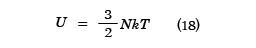
となり、体積Vとは無関係で、温度Tのみによって決まることがわかる。なお、Nkは1モルでは気体定数Rとなる。
[小野昱郎]
開いた系の状態和
これまでは、全体系の質量、あるいは分子数が一定の場合を考察した。以下では、体系の分子数が変化しうる開いた系の状態和を考える。たとえば、水(液相)と水蒸気(気相)が接している場合、液相と気相の分子が相互に出入りして、それぞれの相の分子数が変化しうる。または重力の影響のある大気の密度は高さにより変化しているが、ある高さの部分に仮想的な箱(部分系)を考えると、分子は箱の中とその周囲に自由に出入りして、箱の中の分子数が変化しうる状況にある。このような系を開いた系という。このような状況では、当然、周囲と熱の出入りで、エネルギーの変化も可能である。熱平衡では、その部分系の温度は外界と同じ温度であると同時に、その間の面(界面)での圧力も同じであり、さらに化学ポテンシャルも同じ値である。温度が高いところから低いところへ熱が流れるように、化学ポテンシャルの高いところから低いところへ粒子が流れるから、粒子の出入りがつり合うには、化学ポテンシャルも等しくなる必要がある。
周囲の温度をTとすれば、部分系の微視的状態iが出現する確率は、exp(-Ei/kT)に比例し、さらに、周囲の化学ポテンシャルをμ(ミュー)とすれば、部分系の粒子数Niが出現する確率は、exp(Niμ/kT)にも比例することが導かれる。この重みをつけて状態の和をとった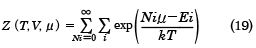
を大きな状態和または大分配関数という。古典系では以下のようになる。
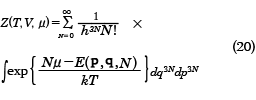
熱力学ポテンシャルΩ(オメガ)は大きな状態和Ζ(ゼータ)と
Ω(T, V,μ)=-kTlogΖ (21)
のような関係があることが知られている。ここで、Ω=-pVであるが、熱力学関係式を用いた別の表式では
Ω=U-TS-μN
となり、これを用いると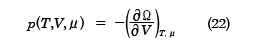
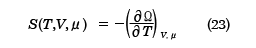
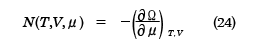
が得られる。(22)式と(23)式は正準集合の分配関数から得られた結果、(10)、(11)式と同等であり、(24)式は平均粒子数Nと化学ポテンシャルμの関係を決める式になっている。ここで、( )A,BはA,Bを一定にしたまま、他の変数で微分をすることを表す。
[小野昱郎]
『C・キッテル著、斎藤信彦・広岡一共訳『統計物理』(1977・サイエンス社)』▽『C・キッテル、H・クレーマー著、山下次郎・福地充共訳『熱物理学』第2版(1983・丸善)』


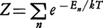 で定義されるZを状態和という。ただし,kはボルツマン定数である。上式のように,すべての可能な状態に関して和をとるので,状態和という名称がつけられた。状態和が計算されると各種の熱力学的な関数が求められる。例えば,ヘルムホルツの
で定義されるZを状態和という。ただし,kはボルツマン定数である。上式のように,すべての可能な状態に関して和をとるので,状態和という名称がつけられた。状態和が計算されると各種の熱力学的な関数が求められる。例えば,ヘルムホルツの