相反定理（読み）そうはんていり

日本大百科全書(ニッポニカ)

相反定理
そうはんていり

一般に、あるM個の物理量を一般化座標x₁,x₂,……,x_Mとし、それぞれに共役な一般化力F1,F2,……,Fnとするとき、それぞれの変化分の間に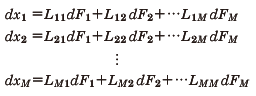

のような関係が成り立ち、さらに比例係数の間にL₁₂＝L₂₁という関係が成り立つ場合を相反関係であるという。このような関係が成り立つことを相反定理という。また、可逆定理、相反性ともよばれる。

　例として、変形を受けた物体中に生ずる力を考えてみる。物体の力のかけ方と引き起こされるひずみの関係は応力テンソルという対称行列で表される。つまり、応力とひずみとの関係に対しても相反定理が成立する。このほか、電気回路における電流と電圧との関係、送信アンテナと受信アンテナとの関係など物理学のさまざまな分野において相反定理が成り立っている。また、散乱断面積の順過程、逆過程での相反性からボルツマンのH定理が示される。

［宮下精二］

オンサーガーの相反定理

物体中に電場を生じさせたときの電流が流れるように、ある外場（電場、磁場など）のもとで流れが引き起こされる現象を輸送現象という。外場が弱いとき、引き起こされる流れは外場に比例する。そのような範囲の現象を線形応答という。そこでの比例係数は輸送係数とよばれる。アメリカの物理学者オンサーガーは、1931年、輸送係数の間の相反関係を導いている。

　たとえば、電位差（電圧）ΔV、温度差ΔTがある状況での電流I_Eと熱流I_Hを考えてみよう。互いに共役な量にするため、（ΔT、I_H）の組を（ΔT、I_H/T＝I_S）にする。ここでI_Sはエントロピー流である。線形応答の範囲で、これらは
I_E＝L₁₁ΔV＋L₁₂ΔT
I_S＝L₂₁ΔV＋L₂₂ΔT
となる。電気伝導度σは温度一定での電位差と電流の比なのでσ＝L₁₁である。それに対し、熱伝導度κは、電流が流れていない場合の温度差と熱流I_H＝TI_Sの比なのでκ＝T(L₁₁L₂₂－L₁₂L₂₁)/L₁₁である。ここでL₁₂やL₂₁は温度差によって電流が流れたり、電位差によって熱流が流れたりするいわゆる交差応答である。これらの間に成り立つL₁₂＝L₂₁という関係が相反関係である。

　この性質は、線形応答の範囲で外場の自由エネルギーへの寄与を考え、時間反転対称性と物理量の緩和が指数関数的（デバイ型）であると仮定すると、一般的にL_ij＝L_jiが成り立つことが示せる。これをオンサーガーの相反定理という。ただし、磁場Hは時間反転に関して符号を変えるため、
L_ij(H)＝L_ij(－H)
となる。この磁場依存性の例として、z方向に磁場がかかった伝導体において、x、y方向の電場、電流を表すベクトルをそれぞれ(E_x、I_x)、(E_y、I_y)とすれば
I_x＝L_xxE_x＋L_xyE_y
I_y＝L_yxE_x＋L_yyE_y
となる。ここでホール効果を考えれば、係数はL_xy＝RH_z,L_xy＝－RH_zとなる。ただし、Rはホール係数とよばれる物質によって決まる定数である。

［宮下精二］

[参照項目] | H定理 | エントロピー | オンサーガー | 散乱断面積 | ホール効果 | ボルツマン

出典　小学館　日本大百科全書(ニッポニカ)

法則の辞典

相反定理【reciprocity theorem，principle of reciprociy】

二つのループアンテナa，bがあり，一方を送信機，他方を受信機と考える．周波数やインピーダンスが不変であるとすると，I_ab/V_a＝I_ba/V_b が成立する．ここで I_ab はaを送信機，bを受信機としたときにbに流れる電流であり，V_a はaに印加される電圧である．同じように I_ba はbを送信機，aを受信機としたときの対応する量である．

相反定理【reciprocity theorem，principle of reciprocity】

音源の存在しない流体媒質の中に2枚の面を想定し，それぞれの面の垂直振動成分を V₁，V₂ としたとき，これによって形成される音圧を P₁，P₂ とすれば，（P₁V₂－P₂V₁）をこの面上で積分した値はゼロとなる．

相反定理【principle of reciprocity】

全電荷 q₁，q₂ をもつ電荷分布によって任意の点につくられる電位をそれぞれ V₁，V₂ としたとき，q₁V₂＝q₂V₁ となるという定理．

相反定理【principle of reciprocity】

線形受動インピーダンスからなる回路網において，ある枝路に印加された電圧と，他の枝路における電流の比は，電圧と電流の一を交換したときの結果生ずる比と大きさ，および位相において相等しい．

相反定理【reciprocity theorem，principle of reciprocity】

一つの可逆電気音響変換器のスピーカーとしての感度と，マイクロフォンとしての感度との比は，その変換器の種類や構造に無関係な定数となる．

相反定理【reciprocity theorem】

双対原理（数学）＊の項を参照．

相反定理【reciprocity theorem，principle of reciprocity】

一般の物理系においては，刺激に対する系の応答を変えることなく入力と出力を交換可能であるという定理．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

相反定理
そうはんていり

「オンサーガーの相反定理」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典