日本大百科全書(ニッポニカ) 「不動点定理」の意味・わかりやすい解説
不動点定理
ふどうてんていり
ある図形Xを自分の中へ写す写像f:X→Xが与えられたとき、f(x)=xすなわちfによって自分自身に写されるようなXの点のことを、fの不動点という。Xやfが適当な条件を満足するときには、かならずfの不動点が存在することを保証してくれるのが、不動点定理である。以下では、写像はすべて連続なもののみを考える。
［野口 廣］
線分や円周と不動点定理
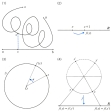
不動点定理についていちばん単純な場合は、Xが線分（これをBで示す）の場合である。すなわち「線分B=［a,b］を自身に写す写像f:B→Bは、fがどんなものであろうと、不動点をもつ」。いいかえれば、写像fによってそれぞれ異なるにせよ、とにかくf(x)=xとなる不動点xが少なくとも1個は存在する。これは直観的には、線分［a,b］をゴム紐(ひも)とし、これをごちゃごちゃと両手でもんで線分上に押し付けてみると、この紐がどんなにごちゃごちゃしていても、かならず元の自分自身の位置の上に押し付けられている点が少なくとも一つ存在するということである（の(1)）。
線分のかわりに、左右に無限に延びている直線Rを考えてみる。するとこの場合には、Rの任意の点xに対して、たとえばf(x)=x+1として写像fを定めると、fはRをR自身の中へ写すが、x≠x+1なので、不動点は存在しない。すなわち、直線では不動点定理は成り立たないのである（の(2)）。同様に円周Sを考える。このとき円周上の任意の点xに対して、f(x)はこの円周をある一定の角αだけの(3)のように回転したものであるとした写像f:S→Sを定めることができる。そこでαが0゜や360゜の倍数でなければけっしてf(x)=xとはならないので、円周Sについても不動点定理は成り立たないことがわかる。
しかし、円周については、不動点定理と類似の次の結果が得られる。円周Sの任意の点xに対して、xを通る直径の反対側の端点x′をxの直径対点ということにしたとき（の(4)）、円周の直径対点の定理「円周Sより直線Rへの任意の写像f:S→Rに対して、f(x)=f(x′)となるような円周上の点xとその直径対点x′との一組が存在する」が成り立つ。そして円周の直径対点の定理からは、次のホットケーキの定理「A、Bを同一平面上にある二つの任意の図形とする。するとそれぞれの図形の面積をちょうど半分に分割する一つの直線が存在する」が証明される。
こうした線分の不動点定理や、円周の直径対点の定理自身は、連続関数についての最大・最小の定理、および中間値の定理から導かれる。
［野口 廣］
円板や球面と不動点定理
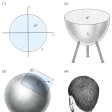
平面R2でB2=｛(x,y)|x2+y2≦1｝で与えられる図形B2が円板である（の(1)）。円板は円周S=｛(x,y)|x2+y2=1｝をその境界としている。空間R3においてはS2=｛(x,y,z)|x2+y2+z2=1｝が球面である。すると、線分、円周の場合と類似に、それぞれ次の定理が成り立つ。円板の不動点定理「円板B2を自身へ写す写像f:B2→B2に対して、少なくとも一つの不動点x、すなわちf(x)=xとなるB2の点xが存在する」、およびボルスク‐ウラムの定理「球面S2より平面R2の中への任意の写像f:S2→R2が与えられたとき、同一のR2の点に写される少なくとも一組の直径対点x、x′が存在する。すなわちf(x)=f(x′)である」。
このボルスク‐ウラムの定理は、円周の直径対点の定理を円周から球面へと拡張したものである。ここで球面上の点xの直径対点とは、xを通る直径の他の端点x′のことである。
この二つの定理から、いろいろな結果が導かれる。以下にその2、3の結果を示す。「円板B2をその境界Sの中へ、Sの各点を不動にするような写像によって写すことはできない」。つまり、太鼓の境界を留めたまま、太鼓の皮を太鼓の枠からは外せない、ということである（「太鼓の皮の定理」の(2)）。
地球を球面とみる。そして同時刻に各地点でそこにおける気圧pと気温tとを測って、この地点に平面上の点(p,t)を対応させる。すると、この対応は球面S2より平面R2への写像であるから、ボルスク‐ウラムの定理により次のことがわかる。「地球では各時間時間にその気温と気圧が一致するような少なくとも一組の直径対点が存在する」。また、ボルスク‐ウラムの定理から次のことも証明される。「A、B、Cは空間内にある任意の三つの立体図形であるとする。このとき、それぞれの立体の体積をちょうど半分に分割する一つの平面が存在する」（ハムサンドの定理）。
球面の各点Pでその点での接平面πPを考える。点Pから出発するこの接平面上の矢印を点Pにおける接ベクトルという（の(3)）。いま、球面上の各点でその接ベクトルが連続的に（すなわち、その向きと長さが連続的に変わる）描かれているとする。これを球面上の接ベクトル場という。このとき、球面の接ベクトル場の定理「球面上のどの接ベクトル場にも、その長さが0のベクトルが少なくとも一つ存在する」が成り立つ。この長さ0のベクトルが出発する点を、このベクトル場の特異点という。この定理は、球面を人間の頭とみ、接ベクトル場を髪の毛とみると、特異点はつむじに匹敵するので、「人間の頭には少なくとも一つのつむじがある」ことを述べている（の(4)）。
［野口 廣］
ブローエルの不動点定理
以上述べた定理は一般の次元に拡張することができる。すなわち、n次元ユークリッド空間Rnを考える。Rnの点xはx=(x1,……,xn)と、n個の実数xiの組xで示される。ここでn次元球体（n=1のときは線分、n=2のときは円板である）Bnとは、Bn=｛x=(x1,……,xn)|x12+……+xn2≦1｝である。またRn+1におけるn次元球面Sn（n=1のときは円周である）とは、Sn=｛(x1,……,xn+1)|x12+……+xn+12=1｝であると定める。
次のブローエルの不動点定理は1910年オランダの数学者ブローエルL. E. J. Brouwer（1881―1966）が発見したもので、線分と円板の不動点定理を一般化したものである。
定理「f:Bn→Bnがn次元球体を自身に写す写像とすると、fは少なくとも一つの不動点xをもつ、すなわちf(x)=xとなる点x∈Bnが存在する」。
ブローエルの定理を証明する技巧を用いて、次の一般次元のボルスク‐ウラムの定理「n次元球面Snよりn次元ユークリッド空間Rnへの写像f:Sn→Rnが与えられると、fによって同一のRnの点へ写される少なくとも一組の直径対点x、x′が存在する。ここで、x=(x1,……,xn+1)のとき、その直径対点とはx′=(-x1,……,-xn+1)である」が証明される。またn次元の太鼓の皮の定理「n次元球体Bnをその境界Sn-1の中へ、Sn-1の各点を不動にしながら写す写像は存在しない」も成り立つ。
ブローエルの定理は、n=2のときにその応用例を示したように非常に強力な定理であるが、1941年に日本の数学者角谷静夫(かくたにしずお)（1911―2004）はこのブローエルの定理を多価写像の場合に拡張した次の定理を証明した。この定理はゲームの理論や経済学などでの基本定理となっている。「n次元ユークリッド空間Rnの任意の有界閉凸部分集合をXとする。FがXの各点をXの閉凸部分集合に対応させる多価写像とすると、x0∈F(x0)となる少なくとも一つのXの点x0が存在する（ここでFは上半連続という仮定を満たすものとする。すなわち、Xの点列｛xn｝がxへ収束し、ynがF(xn)の元であり、｛yn｝がyに収束するとy∈F(x)である）」（角谷の不動点定理）。
［野口 廣］
『野口廣著『不動点定理』（1979・共立出版）』▽『岩野正宏著『不動点定理――常微分方程式への応用』（1985・慶応義塾大学）』▽『高橋渉著『非線形関数解析学――不動点定理とその周辺』（1988・近代科学社）』
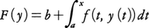を対応させる写像の不動点を求めることにほかならないという事実に着目すれば，常微分方程式の解の存在定理がシャウダーの不動点定理の応用により示される。また，レフシェッツの不動点定理の応用により，次の定理が示される。〈