偏差値（読み）ヘンサチ

デジタル大辞泉

へんさ‐ち【偏差値】

学力などの検査結果が、集団の平均値からどの程度へだたっているかを示す数値。偏差2を10倍し、それを標準偏差で割って50を加えた数として示されるのがふつう。

出典　小学館

精選版 日本国語大辞典

へんさ‐ち【偏差値】

1. 〘 名詞 〙 知能や学力の検査で、その人の得点が全体の中でどの程度の水準にあるかを示す数値。一般には、の式で与えられるＴ得点と称されるものがひろく用いられている。平均は五〇。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

偏差値
へんさち

偏差値とは個人の知能や学力や性格などについての検査結果が、集団の平均値よりもどれくらい上または下に偏っているかを、標準偏差を目盛りとして表すものである。その基本型は、

であるが、この式によると、目盛りが粗すぎるし、平均値以下の場合にマイナス符号をつけなければならない。そこでこれらの不便を解消するために、次式が用いられる。

すなわち、目盛りを10分の1にし、平均値に位置する個人の偏差値を50としている。得点の分布が正規分布（釣鐘のような形）の場合には、たとえば偏差値70以上には上位からの2.28％が、そして40以下には下位からの15.87％が含まれる。

　なお標準偏差とは、得点のばらつきの程度を示すもので、次式によって示される。

ここでΣの記号は、合計することを意味する。そこで標準偏差は、個人の得点と集団の平均値の差（偏差）の二乗和を集団の人数で割った値を開平して求められる。標準偏差は、得点の分布が正規分布の場合には、最高点と最低点の差（範囲）のほぼ6分の1に相当する。

［河合伊六］

偏差値の活用

検査結果の表示法として偏差値が用いられるようになったのは知能検査が最初であろう。知能検査の結果は、従来、精神年齢（MA）や知能指数（IQ）で表示されていたが、成人用知能検査が開発されたころから、知能偏差値が多く用いられるようになった。知能の発達曲線は10歳代の後半から緩やかになり、中・高年になると横ばいもしくは低下を示すので、各年齢ごとの平均値や分布に基づいて、個人の集団内の位置を示す知能偏差値のほうが、精神年齢や知能指数よりも合理的で便利であることが認められたからである。

　その後やがて、偏差値による表示法は学力検査にも適用されるようになった。全国版の標準学力検査や大学入学試験（1989年までの共通一次試験や90年以後のセンター試験）の結果を学力偏差値で示すのはその好例である。これによれば、個人の学力が全国的な規模でどの程度の水準に位置しているかを知ることができるので、1970年代以降は入試の合否の予測のための情報源として活用されている。また、教師が作成した期末試験で、ある生徒の成績が、たとえば、国語で50点、数学で40点のとき（平均点が国語で60点、数学で30点のとき）、その生徒の国語と数学の成績を素点のまま比較しても意味はない。それを比較するには、国語と数学のそれぞれを偏差値という同じ尺度に換算することが必要である。このように、偏差値はたいへん合理的で便利なものであるために、さらに性格検査やその他の得点の表示法として広く用いられるようになった。

［河合伊六］

「偏差値」問題

ところが、偏差値データによる「輪切り選抜」や大学の序列化といった弊害がしばしば指摘されたため、文部省（現文部科学省）は共通一次試験にかわるセンター試験の実施（1990）、業者による統一テストの廃止（1993）など、評価尺度の多元化を進めるに至った。このように、いわゆる「偏差値」問題として、学力偏差値が厳しく批判され、今日の教育のゆがみを引き起こした原因の一つのような言い方がされている。学力偏差値によれば、全国的規模での同じ尺度で評定できるので、合格者のそれを調査し集計することにより学校間の格差は明らかになり、それが学校のランク付けに利用されることは事実である。また、学力偏差値が広く用いられるようになったころから、学力だけで学校や個人を評価する傾向や知育偏重の気運に拍車がかかったことも事実である。しかし、その責任を偏差値に帰すことは妥当ではない。偏差値自体は個人が集団内で占めている相対的位置を表示するだけのものであり、要はその活用の仕方であって、偏差値の誤った用い方をしたことのほうに責任が問われるべきである。このこととは別に、偏差値は得点が正規分布することを前提として考察されたものである。ところが、学業成績（学力）は、教師が優れた指導をすれば高得点者が多くなり、正規分布とはならないはずである。学力偏差値を用いる際にはこの点に留意する必要がある。逆に、本来、正規分布になるはずの得点がそうならなかった場合には、分布を正規分布の形に修正して偏差値を求めることが望ましい。この場合の偏差値はとくにT得点とよばれる。

［河合伊六］

『毎日新聞社編・刊『内申書・偏差値の秘密』（1981）』▽『望月一宏著『偏差値にゆらぐ子供たち』（1984・講談社）』▽『矢倉久泰著『偏差値――「教育天国」日本の妖怪』（1986・教育社）』▽『菊地良輔著『中学生の進路と偏差値問題』（1993・民衆社）』▽『竹内常一著『日本の学校のゆくえ――偏差値教育はどうなるか』（1993・太郎次郎社）』▽『玉利まさる著『偏差値なんて、気にしない』（1994・近代文芸社）』▽『桑田昭三著『よみがえれ、偏差値――いまこそ必要な入試の知恵』（1995・ネスコ）』▽『平井明著『SQの時代――偏差値教育との訣別』（1997・教育開発研究所）』▽『森口朗著『偏差値は子どもを救う』（1999・草思社）』▽『多賀谷光男著『偏差値に罪はない』（2001・四谷ラウンド）』

[参照項目] | 学力 | 学力テスト | 共通一次試験 | 精神年齢 | 大学入試センター試験 | 知能検査 | 知能指数 | 標準偏差

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

偏差値 (へんさち)

日本で用いられる教育統計用語で，テストの点数などの数量的な分布があるとき，次の公式によって個々の数値を変換したものを〈偏差値〉と呼ぶ。分布の平均値がm，標準偏差（ばらつきの程度を示す量）がσであるとき，もとの数値xに対する偏差値yは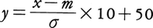，で計算される。このようになおしたyの分布は，いつも平均値が50で標準偏差が10となる。したがって次に述べるように偏差値を用いると，一つの分布の中の各数値の位置づけができるし，いくつかの分布の比較もしやすくなる。

　もとのxの分布が正規分布であれば，yの分布も正規分布であり，そのときは偏差値がわかれば，mやσを知らされなくても，その数値が全体のなかで占める位置がわかる。たとえば偏差値がa以上となる割合は図の灰色の部分の面積で表されるが，それは標準正規分布の表から（a/10）－5以上となる確率として求まる。aが55なら偏差値がそれ以上となる割合は約31%である。

　2種類の分布のそれぞれにおける数値x，x′もこのままでは優劣は比較しがたいが，尺度が標準化されている偏差値y，y′になおせば両者のそれぞれの分布における相対位置を比較することができる。たとえばA君の数学と国語の成績がそれぞれx＝75，x′＝80であったとしよう。クラスの平均値，標準偏差が図中の表のようで，得点が正規分布に近いとすれば，それぞれの課目でA君がクラスの中で占める位置がわかり，また数学の点数は国語の点数より低いが，クラスでの順位では上位を占めていることが知られる。

　分布が正規分布から離れているときは，このような詳しい位置づけはできないが，チェビシェフの不等式を用いるなどして，mやσからおおまかな評価は得ることができる。
執筆者：飛田 武幸　偏差値は今日，教育の世界では学力測定の際の数値として利用され，しばしばその功罪が論議されている。ある一定の学力テストを行い1人1人の生徒の成績をテストを受けた生徒集団の平均点からの偏位でみる偏差値は，得点（素点）の多少にかかわらず，その生徒集団の中での学力の相対的位置を確定するうえできわめて便利なものである。しかし，それが現実の教育のなかで，とくに生徒の進学校の決定の手段に使われるようになると問題化してくる。1970年代，偏差値が教育界に入りこんだのは，中学校の教師が客観的で科学的な資料をもとにして生徒の進学校を決定するようになってからであるといわれている。中学校在籍中に何回か業者による学力テストを実施し，その大量のデータをもとに生徒の学力の相対的な位置を判断すれば，それまで経験と勘に頼っていた進路指導をより客観的に行うことができる。しかし，これは同時に高校の序列化の傾向をもたらした。また偏差値の上下を人間的諸力の評価に置きかえるという錯覚さえ生徒や父母の間に生じさせ，不要な劣等感の形成までもたらす結果になった。さらには，中学校段階で，年に何回も業者テストを実施することから生徒をテスト主義と受験万能の生活に巻き込むことになってしまった。そしてこの傾向に拍車をかけたのが，1979年以降実施された国公立大学共通一次試験だといわれている。今日，国立大学は偏差値でみごとに序列化され，テスト業者の高校時および予備校時に実施するテストの偏差値の的中率の高さは驚くべきものである。

　こうして偏差値は，中学，高校時に2回にわたって利用され，生徒の学力観だけではなく人生観にまで大きな影響を及ぼしている。偏差値が上がることが学力向上であると信じ，受験学力の錬成に懸命になる生徒と学校，またそれを奨励する受験産業，そのなかで生徒は確実に学ぶことの喜び，真理を発見することの楽しみ，みずからの疑問を最後までつきつめることの楽しさを見失っていく。しかし，この問題の解決は簡単ではない。偏差値によらない進路指導が実現されるには，高校間の格差の是正，入試制度の抜本的改善および大学間の序列化の解消が行われなければならない。さらに学歴偏重の社会的風潮を改めるなど，偏差値問題については，日本の社会構造の根本にかかわる改革を要求されているのである。
執筆者：村越 邦男

図－偏差値

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

偏差値【へんさち】

日本で用いられる教育統計用語で，学力測定の際の数値として利用される。ある受験者の得点とそのテストの平均点との差を標準偏差（ばらつきの程度を示す量）で割り，その値の10倍に50を加える。これにより，その受験者の成績を平均点からの偏位でみることができ，得点の多少にかかわらず受験者全体の中での相対的位置を簡便に知ることができる。1970年代から日本の教育界で一般的に用いられるようになったが，これが受験競争と結びつき，大量の生徒の参加する学力テストに利用されると，生徒たちを序列づけ，また受験する高校，大学などをランクづける，〈客観性〉に富んだきわめて強力な武器となった。多様な尺度・観点をもつべき学力評価が偏差値に一元化され，また偏差値の上下が人間的諸力の評価であるかのような錯覚すら生まれている。このため文部省は，1993年中学校での業者テスト実施を禁じ，1994年の高校入試は脱偏差値入試元年として話題となった。その後も文部省は高校に総合学科を設けたり入試科目を減少したりさまざまな施策を講じているが，進学塾による偏差値教育と受験戦争は相変わらずである。→教育評価
→関連項目業者テスト

出典　株式会社平凡社

大学事典

偏差値
へんさち

知能や学力等の試験において，個人の成績が被験者集団の中でどの程度の位置にあるかを，集団の平値からどの程度隔たっているかによって示す数値。日本では一般に，

で算出される値が用いられ，平値に位置する個人の偏差値は50となる。標準偏差とは得点のばらつきの程度を示すもので，

で示される。検査結果の表示法として偏差値が用いられるようになったのは知能検査が先だが，やがて学力検査でも用いられるようになった。1970年代以降，入試の合否の予測のための情報源として活用されている。これは個人の学力が全国的な規模でどの程度の水準に位置しているか，偏差値を通して把握できるためである。しかし，偏差値による「輪切り選抜」や「大学の序列化」といった問題が指摘されるようになり，文部省（当時）は共通一次試験の廃止と大学入試センター試験の実施など，評価尺度の多元化を進めたが，依然として偏差値は受験の際の判断材料として重視されている。偏差値自体ではなく，その活用の仕方が問題と指摘される。
著者: 齋藤千尋

出典　平凡社「大学事典」

ブリタニカ国際大百科事典 小項目事典

偏差値
へんさち
standard deviation score

標準偏差を尺度とし，個々の測定値が代表値から逸脱している度合いを示す数値。算出の公式は偏差値 T＝10(X－M)/σ＋50 (ただし X はある測定値，M は平均，σ は標準偏差) 。標準検査 standardized testは知能や学力の測定値が正規分布を示すとの仮定に立って，個々の児童の相対的位置を偏差値で表わすことが多い。 40≦T≦60 に約 68%のものが入る。これを偏差値法と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典

ブランド用語集

偏差値

偏差値とは平均を50、標準偏差を10となるよう各データを変換し、集団内における各データの位置を表した値をいう。たとえば偏差値70は平均＋標準偏差×2として計算される。正規分布の仮定を置くことによって、偏差値からそのデータが全体の上位（ないし下位）何パーセント以内に含まれるかを知ることができる。

出典　(株)トライベック・ブランド戦略研究所