因果分析（読み）いんがぶんせき（その他表記）causal inference

最新 心理学事典

いんがぶんせき
因果分析
causal inference

諸科学におけると同様に，心理学の目的は関心のある現象の因果関係を解明することにある場合が多い。因果分析とは，独立変数と従属変数の因果関係について実証データから分析を行なうことである。

【因果関係と独立変数の操作性】　「相関関係と因果関係は異なる」といわれるが，しばしば独立変数independent variableを操作することで従属変数dependent variableが変化することを確認する「独立変数の操作性」こそが因果関係を示す要件であるとされ，独立変数を操作する実験研究experimental studyこそが，因果関係を示す方法論であると考えられることがある。実際，自然科学のうち化学・工学・生物学の一部など実験研究が可能な分野では，実験研究以外の方法はほぼ利用されない。たしかに無作為化を伴う実験研究を行なえば，独立変数以外の要因による従属変数への影響を除去できるため，研究の内的妥当性internal validity，つまりその研究で得られた従属変数と独立変数の関係についての知見の確かさの程度を高めることができる。

　しかし，「操作性のある研究のみが因果関係の同定を可能にする」という素朴な考え方に立てば，たとえば月と潮の満ち引きのような，物理学で確立され，工学で実際に利用されているようなレベルの関係ですら「月の位置を研究者が操作していないため因果関係といえない」ということになる。

　また，因果に関する哲学的議論では，一般的な因果関係を個別の事例から帰納法によって示すことはできないとする「帰納の問題」がよく知られている。より科学研究の文脈に即して述べるならば，実験研究を行なったとしても，そこで得られた因果関係は厳密には実験対象にのみ限定されるべきものであり，それ以外の同様の対象にも適用ができるとする自然の斉一性原理principle of the uniformity of natureの仮定が成立することを示すのは難しい。心理学研究においては低次の知覚処理など，人間すべてで機能が共通する可能性が高いと暗黙に想定されている分野では，自然の斉一性原理に従って研究パラダイムが構成されている。一方，個体差を扱う教育心理学や社会心理学ではこの原理を仮定するのは難しいことから，対象を限定した実験研究を行なうよりも，大規模な調査や観察を行なう方が，研究結果を得られた標本以外に適用できる程度を示す外的妥当性external validityの高い一般的な関係を示すことができる可能性がある。

　加えて心理学では，観察研究や調査研究の方が自然な状況でのデータが得られる可能性が高く，独立変数を操作する実験研究の生態学的妥当性ecological validityについても注意が必要である。上記の議論を考えると，実験研究のみが因果関係を立証できるという考え方は必ずしも正しいわけではなく，また因果関係と相関関係を明確に区別することは難しい。因果関係は背後に存在するメカニズムや，再現性や予測力，他の因果関係との関連などさまざまな観点から得られた証拠全体から総合的に判断していくべきである，と考えるのがいちばん自然な態度である。

【因果効果の定義】　因果関係とは何かという哲学的な議論はともかく，「独立変数以外の要因が除去された，独立変数単独の従属変数への効果」を操作的に定義して利用し結果を吟味していくことが重要である。ここでは研究法の種類とは無関係に定義され，最もよく利用されているルービンの因果モデルRubin causal modelに基づく因果効果の定義を紹介する。

　簡単にするために独立変数ｚは2値であるとし，たとえば特定の操作を行なわない場合（対照群）をｚ＝0，特定の操作を行なう場合（実験群あるいは介入群）をｚ＝1とする。ここでもし研究対象がｚ＝0に割り当てられた場合に得られる値をｙ⁰，ｚ＝1に割り当てられた場合に得られる値をｙ¹とする。つまり従属変数ｙの値は本来二つ存在するはずであり，このとき「ｙ¹－ｙ⁰の母集団平均」を独立変数ｚの従属変数ｙへの因果効果causal effectと定義する。この量は「同じ個人内での，介入群に割り当てられた場合の結果と対照群に割り当てられた場合の結果の差」の母集団平均であることから，独立変数以外の要因が除去された独立変数ｚ単独のｙへの効果，つまり因果効果であると考えることができる。

　ただし，ｙ⁰とｙ¹は潜在的な結果変数potential outcome，つまりｚ＝0の場合にはｙ⁰が観測され，ｙ¹は欠損値missing valueとなり，一方ｚ＝1の場合にはｙ¹が観測され，ｙ⁰は欠損値となっているため，因果効果の推定を簡単に行なうことができないという因果推論における根本問題fundamental problem of causal inferenceが存在する。

　ここで，ｚを無作為に割り当てる実験研究の場合には，通常の群間差，つまり



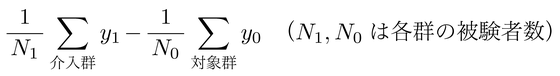
は被験者数が増えるにつれて，



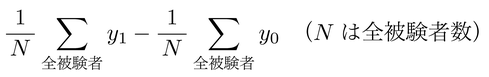
つまり標本での因果効果と等しくなることを示すことができる。すなわち，無作為割当を伴う実験研究での群間差は因果効果の良い（統計学的には不偏な）推定値である。逆にいえば，実験研究における実験条件の効果量として群間差を求めることで，因果効果を推定していることになる。

　一方，独立変数ｚを無作為に割り当てられない場合には，たとえ被験者数を増やしても，通常の群間差は因果効果とは等しくならない。たとえば

介入群での平均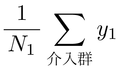と

対照群での平均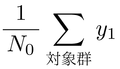は

被験者数を増やしても等しくならないからである。

【因果効果の推定の条件】　実験研究にせよ，調査や観察などの非実験研究にせよ，独立変数ｚ単独のｙへの効果である因果効果を正しく推定することが因果関係の理解につながるとするのが，近年の統計的因果推論statistical causal inferenceの考え方である。では調査研究や観察研究において因果効果を推定することは可能であろうか。この問いに対して，ローゼンバウムRosenbaum,P.R.とルービンRubin,D.B.（1983）は無視できる割当strongly ignorable treatment assignment条件が成立すればよいことを示した。これは，「従属変数と独立変数どちらにも影響を与える共変量covariate（ｘとする）によって独立変数の割り当てを説明できる」という条件である。これが成立している場合には，共変量ｘを利用した統計的な共変量調整法covariate adjustmentによって因果効果を推定することが可能であることが示されている。

【非実験研究での因果効果の推定法】　調査研究や観察研究で因果効果を推定する方法として，以下がある。

⑴マッチングmatching（均衡化）　群間で共変量の値が（ある基準で）同じ，あるいは近い対象者のペアを作り，このペア間の差の平均を計算する。

⑵恒常化・限定（サブグループ解析）　共変量のある特定の値の対象者のみに限定して解析を行なう。

⑶層別解析stratification analysis　共変量の値をいくつかの層に分け，層ごとで二つのグループがその共変量の値について等質になるようにし，比較した結果を統合する。

⑷回帰モデルの利用　共変量ｘと独立変数ｚの両者を説明変数とし，従属変数ｙを説明する回帰モデルregression modelを利用する。とくに共変量と従属変数に交互作用を仮定しないモデルを共分散分析モデルanalysis of covariance modelとよび，説明変数の偏回帰係数が因果効果の推定値になる。

⑸傾向スコアpropensity scoreの利用　モデル仮定を極力行なわないノンパラメトリックな方法の一つで，共変量によって説明される割当の確率＝傾向スコアを用いて共変量調整を行なう。具体的には傾向スコアを用いてマッチングを行なう，層別解析や逆数による重みづけを行なうなどの方法が利用される。

　⑴から⑶の方法は，無視できる割当条件の成立のために多くの共変量が必要となる場合には利用することが難しい。たとえばマッチングであれば，複数の共変量について同じあるいは近いペアを作成することは難しい。また回帰モデルでは，回帰関数の線形性や交互作用項の有無などモデルの仮定が誤っている場合に因果効果の推定に大きなバイアスが生じることから，近年では傾向スコアなどノンパラメトリックな方法が盛んに利用されている。

　独立変数が2値以上の場合も，ダミー変数の組み合わせとして考えることで，上記と同様の議論や解析が可能になることが知られている。　→回帰分析　→実験計画法　→実験法　→心理学方法論
〔星野 崇宏〕

出典　最新 心理学事典