交代式（読み）コウタイシキ

デジタル大辞泉

こうたい‐しき〔カウタイ‐〕【交代式】

有理式において、その中の任意の二つの変数を交換すると、式の符号だけが変わった式となるもの。

出典　小学館

精選版 日本国語大辞典

こうたい‐しきカウタイ‥【交替式】

1. 〘 名詞 〙 令制で、中央、地方の官吏の交替事務監査に必要な諸規則を集成したもの。「延暦交替式」（八〇三）「貞観交替式」（八六八）「延喜交替式」（九一一‐九二一）などがあり、「新訂増補国史大系」に所収。一般に、式は律令の施行細則であるが、交替式の内容には格をふくみ、交替事務管掌の勘解由使一職司の執務内容に限られている。

こうたい‐しきカウタイ‥【交代式】

1. 〘 名詞 〙 数学で、二つ以上の文字を含む整式または分数式で、その中のどの二つの文字を入れかえても、もとの式の符号を変えた式になるもの。たとえば x-y など。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

交代式
こうたいしき

n個の変数x₁、x₂、…、x_nの多項式において、任意の二つの変数を交換すると、もとの式の符号だけを変えた式が得られるとき、その式はx₁、x₂、…、x_nに関する交代式であるという。たとえば、二つの変数x、yの多項式
　　f(x, y)＝x³－x²y＋xy²－y³
のxとyを入れ換えて新しい多項式をつくる。

　　f(y, x)＝y³－y²x＋yx²－x³
この多項式はもとの多項式f(x, y)に－1を掛けたものになる。つまり
　　f(y, x)＝－f(x, y)
　このような多項式の性質を、変数を増やして考えたものが交代式である。つまり、n個の変数x₁、x₂、…、x_nの多項式f(x₁, x₂,…, x_n)で異なるiとjに対し、x_iとx_jを入れ換えると、もとの多項式f(x₁, x₂,…, x_i,…, x_j,…, x_n)からf(x₁, x₂,…, x_j,…, x_i,…, x_n)ができる。この二つの多項式を比べたとき、
　　（＊）　f(x₁,…, x_i,…, x_j,…, x_n)＝－f(x₁,…, x_j,…, x_i,…, x_n)
が任意の相異なるiとjに対して成り立つとき、この多項式fを交代式という。（＊）のかわりに
　　f(x₁,…, x_i,…, x_j,…, x_n)＝f(x₁,…, x_j,…, x_i,…, x_n)
が成り立つのが対称式である。

　二つの交代式の和、差はまた交代式であるが、積は対称式になる。また、対称式と交代式の積は交代式である。n変数の交代式でいちばん簡単で重要なものは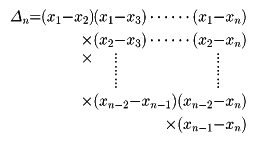

である。このΔnは1≦i＜j≦nなるすべてのi、jに対し、差(x_i－x_j)をつくり、その積をとったものであるから、差積といわれる。たとえば
　　Δ₂＝x₁－x₂,
　　Δ₃＝(x₁－x₂)(x₁－x₃)(x₂－x₃)
である。（＊）式でx_i＝x_jと置いてみると
　　f(x₁,…, x_i,…, x_i,…, x_n)＝－f(x₁,…, x_i,…, x_i,…, x_n)
となり、f(x₁,…, x_i,…, x_i,…, x_n)＝0を得るから、交代式f(x₁,……, x_n)はx_iの一変数多項式として解x_jをもち、(x_i－x_j)で割り切れる。したがって任意の差(x_i－x_j)(i＜j)で割り切れるから、それらの積である差積Δnで割り切れる。

　　f(x₁,……, x_n)＝Δn・s(x₁,……, x_n)
なる多項式s(x₁,……, x_n)を考えると、fとΔnは交代式であるから、sは対称式になる。ここで対称式の基本定理を使うと、sは基本対称式s₁、s₂、……、s_nの多項式になる。ここで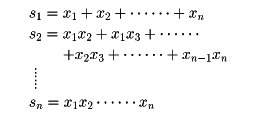

である。ゆえに任意の交代式は、基本対称式の多項式と差積の積になる。この結果は交代式の因数分解などに使われる。たとえば
　x³－x²y＋xy²－y³
は交代式であるからΔ₂＝x－yで割り切れる。実際割り算を行って、商x²＋y²を得るから
　x³－x²y＋xy²－y³
　 ＝Δ₂(x²＋y²)＝Δ₂(s₁²－2s₂)
となる。

［菅野恒雄］

[参照項目] | 対称式

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

交代式 (こうたいしき)
alternating expression

3変数の多項式f（x，y，z）＝x²y－y²x＋y²z－z²y＋z²x－x²z，g（x，y，z）＝x⁴y－y⁴x＋y⁴z－z⁴y＋z⁴x－x⁴z－x³y²＋x²y³－y³z²＋z³y²－z³x²＋x³z²において，xとyを入れかえると，符号が変わって，それぞれ－f（x，y，z），－g（x，y，z）となる。yとzあるいはzとxを入れかえても同じである。このような多項式のことを交代式と呼ぶ。一般にn変数の多項式f（x₁，……，x_n）のうちで，変数x₁，……，x_nの順序を入れかえたとき，f（x₁，……，x_n）か－f（x₁，……，x_n）となるもので，対称式でないものを交代式という。これは任意の二つの変数を入れかえると符号が変わるということで特徴づけられる。多項式，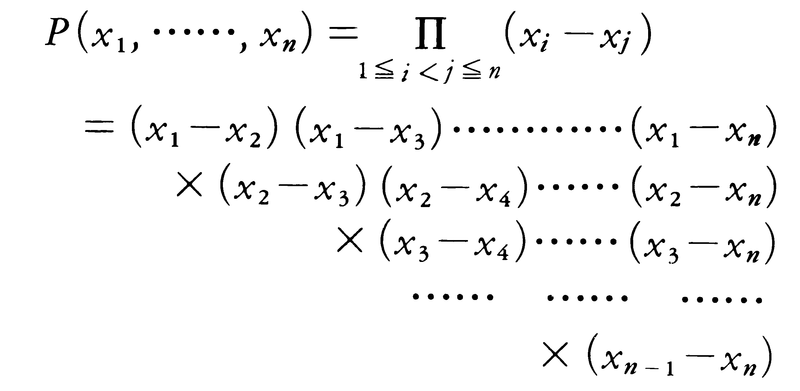

は差積と呼ばれる。差積は交代式であり，すべての交代式は差積と対称式の積になる。したがって，差積はもっとも簡単な交代式であり，その意味で最簡交代式とも呼ばれる。交代式の偶数個の積は対称式であり，奇数個の積は交代式である。交代式と対称式の積は交代式である。
執筆者：丸山 正樹

交替式 (こうたいしき)

平安時代初期，内外官の交替に関する規則を集成した法規集。《延暦交替式》《貞観交替式》《延喜交替式》の3種があり，いずれも勘解由使（かげゆし）によって編纂された。奈良時代には，外官（地方官）たる国司の交替に際し，後任の国司が前任の国司から事務引継ぎを受けるに当たって，一種の会計監査を行い，前任国司は解由（げゆ）という監査済の証明書をもらって都に帰任するしくみになっていた。この解由制がしだいに強化されると，国司の交替に際して種々の紛糾を生じ，交替の円滑を欠くようになった。そこで769年（神護景雲3）に国司の監察と争訴の受理とを主たる職掌とする勘解由使という令外官（りようげのかん）が設置されたが，この勘解由使が国司交替の際の事務引継ぎに関する疑義をなくし，勘解由使の勘判の基準を定めるために803年（延暦22）に撰進したのが，《延暦交替式》正確には《撰定諸国司交替式》1巻である。その内容は国司の交替に関する格，勅をそのままの形で引載し，いわば〈格〉的な体裁をとっている。その施行の時期は明らかでないが，時を移さず施行されたと見てよい。その後809年（大同4）に解由の制度は内官（京官）にも拡充され，867年（貞観9）には《貞観交替式》正確には《新定内外官交替式》2巻が撰進され，翌868年に施行された。

　これは先行の《延暦交替式》を土台として，これに追加，加筆する方法で編纂された。上巻は亡失し，下巻のみが現存する。ついで911年にさらに交替式改訂の作業がはじまり，921年（延喜21）に《延喜交替式》正確には《内外官交替式》1巻が撰進された。

　この交替式は体裁も大いに整備され，〈律〉〈令〉〈式〉と同様に〈凡〉字を冠した条文構成をとったものであるが，その施行の年月も明らかでなく，10世紀初頭という時代では，《延喜式》などとともに，どの程度の実効力を有したかは疑問である。《貞観交替式》上巻を除く3交替式は《新訂増補国史大系》に所収。
執筆者：虎尾 俊哉

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

交代式
こうたいしき
alternating expression

n 個の文字 x₁，x₂，…，x_n の整式，あるいは有理式 F(x₁，x₂，…，x_n) において，任意の2変数 x_i，x_j を取替えると，もとの式と符号だけが変るとき，すなわち，

F(x₁，…，x_i，…，x_j，…，x_n)＝－F(x₁，…，x_j，…，x_i，…，x_n)

が成り立つとき，式 F を x₁，x₂，…，x_n の交代式という。たとえば，x₁－x₂＝－(x₂－x₁) であるから，x₁－x₂ は交代式である。差積 D(x₁，x₂，…，x_n)＝Π_i＜j(x_i－x_j) は交代式で，一般の交代式は

F(x₁，…，x_n)＝D(x₁，…，x_n)G(x₁，…，x_n)

と，差積と対称式 G との積として表わせる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

交替式【こうたいしき】

平安時代初期，外官(げかん)（地方官）・内官(ないかん)（京官）の交替に関わる法令などを集成した法規集。国司の交替時の監察等に当たる勘解由使(かげゆし)により編纂され，〈延暦交替式(えんりゃくこうたいしき)〉〈貞観交替式(じょうがんこうたいしき)〉〈延喜交替式(えんぎこうたいしき)〉がある。〈延暦交替式〉（正式名称は撰定諸国国司交替式）１巻は803年の撰進。国司の交替に関係する格(きゃく)などをそのまま収める。〈貞観交替式〉（正式名称は新定内外官交替式）２巻は867年撰進，868年施行。〈延暦交替式〉に追加する形で編纂され，在京諸司についても扱う。上巻は散逸し下巻のみ残る。〈延喜交替式〉（正式名称は内外官交替式）１巻は911年編纂開始，921年撰進。内容は192条の〈凡〉で始まる条文に改められている。

出典　株式会社平凡社