標本調査（読み）ヒョウホンチョウサ（英語表記）sample survey

デジタル大辞泉

ひょうほん‐ちょうさ〔ヘウホンテウサ〕【標本調査】

標本抽出をして調査を行い、その分析から確率論的に全体を推測する方法。サンプリング調査。→全数調査

出典　小学館

精選版 日本国語大辞典

ひょうほん‐ちょうさヘウホンテウサ【標本調査】

1. 〘 名詞 〙 統計学的な調査または調査方法の一つ。母集団から見本として抽出された資料について調査し、その結果から確率論によって全体を推測すること。また、その方法。サンプリング調査。〔推計学の話（1949）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

標本調査 (ひょうほんちょうさ)
sample survey

日本の人口や雇用労働者の平均賃金を知る場合などのように，特定の集団を観察してその特徴を数量的に把握する調査を統計調査という。対象となる集団のすべての構成要素を観察する統計調査が全数調査と呼ばれるのに対し，構成要素の一部分しか観察されない統計調査は標本調査と呼ばれる。標本調査は，構成要素の抽出が確率的に行われるか否かによって，無作為抽出法（ランダム・サンプリング）と有意抽出法とに二分される。有意抽出法には典型調査，割当法，アンケート法などがあり，歴史的にも先行するが，方法の未成熟や欠陥のため現在ではあまり重視されない。このように本来は有意抽出法，無作為抽出法のどちらの抽出法によるものも標本調査であるが，無作為抽出法が多用される今日では，単に標本調査といえば無作為抽出法による標本調査を意味することも多い。無作為抽出法には，もっとも基礎的な抽出法である単純無作為抽出法のほか，層化抽出法，多段抽出法，系統抽出法などの諸技法が考案されているが，以下ではまず単純無作為抽出法を例にとってその原理を説明する。

単純無作為抽出法の原理

たとえば，10人勤めている会社があってその平均賃金を知りたいものとする。平均をもっとも正確に知る方法は10人全員の賃金を調査することで，これが全数調査である。その結果，たとえば表1のような数値が得られたとすると，平均賃金μは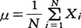，つまり，1番目から最終のN番目の人までの賃金の和を人数Nで割って求められるから，いまの場合5万円になる。このとき，全体の平均を推定するために，たとえば5人だけ調べるのが標本調査である。このように一部分の観察に基づいて全体を推し測ることは日常生活の中でも無意識のうちに実践されており，みそ汁の味見などはその好例である。ところで，小さじ1杯の味でなべ全体の味加減を的確に予測できるのは，実は，事前によくかき混ぜることによって，味に関してどの部分も均質な状態にしたという事情による。人間などのように直接かき混ぜることのできないものを対象にする場合には，対象に一連番号をつけたと想定して手もとの番号札をかき混ぜ必要な数だけの番号札をとり出し，該当する番号の対象者を選び出すことにすれば，対象をかき混ぜたことと同義になる。さらに，あらかじめ0～9までの10種類の数字を記入したカードを用意し，それをかき混ぜてでたらめにとり出して数字を記録したもの（乱数表という）を作っておけば，調査のたびに番号札を作る手間を省くことができる。表2はこうして作った乱数表の一部を例示したものである。表1の例の場合にA～Jに順に1，2，……，9，0という一連番号をつけたと考えて，この乱数表の先頭部分（1行1列）を横に読んで5人とり出せば，D，E，H，F，Jの5人が当たることになる。このとき，とり出された要素を標本（サンプル），その数を標本数（サンプル・サイズ），標本がとり出された母体（標識の集り，この例では賃金の集り）を母集団と呼ぶ。

　上で選ばれた標本に基づいて標本平均xを計算すると，x＝（4＋4＋7＋4＋9）/5＝5.6（万円）になる。したがって得られたこの標本平均をそのまま用いて〈母集団の平均（母平均）は5.6万円〉と推定するとすれば，真の母平均（この場合は5万円）に対して誤った推定値を与えることになる。この例の場合，標本のとり出し方は₁₀C₅（＝252）通りあるから，標本平均xもそれに応じて表3のように変動する。そこで，どのような値の標本平均xがどのような割合で得られるのか（標本平均の分布）を見るために，表3のxをその値ごとに整理してみると，図1のようになる。この図から，母平均を1点で推定する（点推定という）とすれば，母平均μ＝5（万円）をぴったりいい当てられるのは36/252の割合にすぎないことがわかる。そこで推定値に幅をつけて，たとえば〈母平均は3.8～6.2万円〉という推定の仕方をするとすれば，はずれる場合の数は両端の12（＝3＋2＋1＋1＋2＋3）通りだけであるから，はずれる確率は12/252（＝0.048）に減少する。このように幅をつけて区間によって推定する方法を区間推定，このときの区間を信頼区間，当たる確率を信頼係数という。この信頼係数を知るためには，一般には，母集団の各要素の値が未知の場合にも標本平均の分布がわからなければならない。これを保証するのが中心極限定理である。この定理によると，母集団の分布がどんな形をしていてもその平均μと分散σ²が既知なら，無作為に数多くの標本をとりさえすれば，標本平均xは近似的に母平均μに一致する平均をもち，分散σ²/nをもつ正規分布に従う。正規分布においては，（平均－2×標準偏差，平均＋2×標準偏差）という区間の面積が約0.95である。なお，標準偏差はデータのちらばり方の程度を示す尺度である分散の平方根をとったものである。したがって，母集団からn個の無作為標本を抽出し標本平均xを計算する実験を無限に繰り返したとすれば，それらのxの約95%は図2の点線の帯内に相当する区間 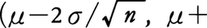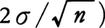に入る。xを中心に考えると，図2でxがこの帯の中に入っているとき区間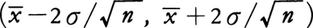は母平均μを含む。したがって，母分散σ²が既知のとき，無作為抽出標本の結果に基づいてこのような区間をつくればそれらの95%は母平均μを含むことになる。こうして信頼係数0.95のμの信頼区間を定めることができる。なお，実際には母分散σ²が未知の場合が多いが，このような場合には標本から求められる標本分散で代用される。また，表1の例の場合には母集団の要素の数Nも標本数nも小さいので中心極限定理を適用することはできないが，N＞300，n＞30程度であれば中心極限定理が成り立つと考えて上のような信頼区間を設定しても実用上大きな問題はないとされる。

標本調査法のおもな技法

上のような区間推定によって誤った推定を行う確率を一応小さくすることはできる。しかし実際の調査で得られるのはただ1組の標本であるから，そのときの標本平均がx₅のように図2の帯からはずれていれば信頼区間を設定してもその区間は母平均μを含まない。信頼係数を0.95とすると，このような可能性が5%は残る。この可能性をゼロにするためには全数調査をするしかない。しかし一定の標本数の下で標本特性値のばらつき（分散）を小さくすることは可能である。たとえば表1の例の場合，賃金の高い人ばかり選ばれたり，逆に安い人ばかり選ばれたりするような抽出法を避ければ標本平均の分散を小さくすることができる。そこで10人全体から一挙に5人選ばないで，たとえば全体を二つの層に分け，A～Fから3人，G～Jから2人という形で5人選ぶことにすれば，₆C₃×₄C₂（＝120）通りの標本のとり出し方が可能で，このときの標本平均xの分布は図3の実線のグラフのようになる。点線のグラフは図1と同じものであるから，前項の抽出法による場合よりxのばらつき方が縮小している。たとえば，前項の抽出法の下ではxが3.8～6.2（万円）に含まれる割合が約0.95であったのに対して，この抽出法の下ではxが4.6～5.4（万円）の間に入る割合がほぼ等しく0.95であり，同じ信頼水準の下での区間がかなり狭くなっている。このように母集団をいくつかの層に分け，各層から独立に標本をとり出す方法を層化無作為抽出法という。これに対して，前項の抽出法を単純無作為抽出法という。一般に，層化に当たって，各層の内部では等質な要素が含まれるように，各層間では異質になるようにすればするほど標本平均の分散を小さくすることができ，推定精度を向上させることができる。なお，実際に層化を行う場合には，調査事項そのものを用いた層化は無理だから，利用可能な台帳に含まれた情報に基づいて，調査事項と密接な関係をもつと考えられる標識に関して層化を行えばよい。たとえば表1の例の場合には対象者の地位や年齢を用いるのが実行可能な良策であろう。

　次に，実際の抽出に当たって標本ごとにいちいち乱数を引くことはまれで，系統抽出法の一種である等間隔抽出法が用いられることが多い。これは母集団の要素数Nを標本数nで割ったときの商N/nより小さい乱数kを一つ選びそれに相当する要素を第1の標本とし，以下k番目ごとに標本を順にとる方法である。この抽出法は，N/nを整数とすれば，母集団をn層に分け各層から標本を一つずつとる方法と見ることができるから一種の層化抽出法とみなすことができる。したがって，通常は単純無作為抽出法より精度が高いという長所をもっている。

　さらに，大規模な標本調査で多用される技法として多段抽出法がある。これは，たとえば全国の世帯の中から標本をとるとき，世帯を直接抽出しないで，まず全国の市区町村の中から一部の市区町村を選び，次に選ばれた市区町村で一部の世帯を選ぶというように，何段階かの異なる抽出単位（市区町村，世帯など）の抽出を繰り返し，最後に目的の抽出単位を抽出する方法である。このとき，最終抽出単位に至るまでの段数に応じて2段抽出法，3段抽出法などと呼ばれる。多段抽出法は，全国の世帯から直接世帯を抽出するのでは調査費用がかさむからというように，通常は，調査地域の分散化，一様化を避けることによる費用の節減をねらって採用されることが多い。したがって，この方法は段数の増加に伴って標本のとられうる範囲をせばめ，精度の低下を招くという短所をもっている。

　ところで，現実の大規模な無作為抽出調査では，層化多段無作為抽出法のように，前述の技法を複雑に組み合わせた抽出法がとられることが多い。したがってこのような場合には推定誤差の評価に単純無作為抽出法の場合の標本誤差を直接適用することはできず，一般にそれより大きくなる。しかし無作為抽出法の眼目は，推定誤差の値そのものの評価が困難な場合でも，乱数表のような客観化された手段を用いて各抽出単位の抽出を行い，それによって母集団の構成要素をかき混ぜることを通じて母集団分布の縮図をつくり出すとともに定量的な誤差評価の可能性を保持する点にある。たとえば割当法では，母集団の組分けに採用されなかった標識に関しては得られた標本が偏りをもつことが懸念されるが，層化抽出法ではそれが防げると考えられるのは，無作為に多数の標本をとることによって，層化に用いられなかった標識に関しても母集団の縮図をなすことが期待されるからである。

　最後に，無作為抽出法の効用は無作為に標本を抽出することによる標本特性値の変動の評価に関与しているにすぎないのであるから，この抽出法に基づいたとしても統計調査の結果数値につきまとう種々の調査誤差の中のただ1種類の誤差を評価できるにすぎず，他の種々の調査誤差の影響からまぬがれることはできない。すなわち，無作為抽出法の推定値は，特定の調査法の下で全数調査を行ったときに得られると仮想される値に対する推定値にほかならない。
→抽出法　→無作為抽出
執筆者：坂元 慶行

表1～表3，図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

標本調査
ひょうほんちょうさ
sample survey

サンプリング調査ともいう。統計的調査には全数調査と標本調査とがある。調査対象全体について一つ一つ調査するのが全数調査である。これに対して、調査対象の一部を抜き出して調査し、その結果から調査対象全体の性質を推測するのが標本調査である。全数調査が簡単に実行できればそれでよいが、全数調査が不可能なこともある。また不可能でないにしても、費用、労力、時間などの面で現実問題として不適当なことが多い。このような場合に標本調査が利用される。

　標本調査の場合に、もとの調査対象全体を母集団とよび、もとの調査対象から抜き出された一部分（それについて調査する）を標本とよぶ。母集団の大きさとは母集団の構成要素の個数であり、標本の大きさとは標本の構成要素の個数である。

　標本調査では、母集団から抜き出した標本だけについて調べるのであるから、標本が偏ったものであってはならない。母集団の性格がよく反映されるように標本を選ばなくてはならない。この場合、母集団に関する知識はできるだけ効果的に活用する必要がある。調査を企画する人が、自分の知識や経験を生かしてもっとも代表的と思われる標本を選ぶ方法がある。この方法を有意抽出法という。この方法で選ばれた標本が母集団の性質をよく反映しているという客観的保証がある場合はよいが、そうでない場合は偏った標本が得られる危険性がある。

　現在は、母集団に確率分布を導入し、確率的に抜き出した標本を用いる方法が標本調査法として広く用いられている。この方法の長所は、標本による誤差を合理的に推定できること、また精度に関する要求に見合った調査が可能になることなどである。

　もっとも簡単な場合として、母集団が等質であると考えられるとき、母集団のどの要素も同じ確率で抜き出されるようにする抽出法がある。この方法を（単純）無作為抽出法という。

　実際に大きさNの母集団から大きさnの標本を無作為抽出するには乱数表を用いるのが普通である。その方法を説明しよう。ここではN=486,n=20としておく。乱数表の任意の数字から始めて、次々に3桁(けた)でくぎってゆく。そうすると001,002,……,999,000が同じ確率で現れてくる。ここで487,488,……,999,000が出た場合にはそれを飛ばしてゆく。また同じ3桁の数が出たときもその数は飛ばしてゆく。こうしてできる3桁の数の系列から初めの20個をとればよい。

　次に母集団がいくつかの異質の部分母集団よりなる場合について考えよう。母集団がいくつかの互いに共通部分のない部分母集団に分割されるとき、この部分母集団のことを層とよぶ。層の数がk個あって、各層から独立にそれぞれ大きさn₁、n₂、……、n_kの標本を単純無作為抽出すると、もとの母集団から大きさn(n=n₁+n₂+……+n_k)の標本が得られたことになるが、このような方式を層別無作為抽出法という。この場合にもとの母集団の大きさをN、各層の大きさをN₁、N₂、……、N_kとするとき、各層の標本の大きさn_iを層の大きさN_iに比例するようにとる方法を比例割当法という。

　また、大きさNの母集団から大きさnの標本を抜き出すのに系統的抽出法または等間隔抽出法とよばれる方法がある。この方法では、母集団の要素全体に一連番号をつけておき、初めの一つの番号だけを無作為に選び、あとは一定間隔の番号のものを選んで全体がn個になるようにするのである。この方式は、通行人から聞き取り調査をする場合、病院へきた患者からその一部を抽出調査をする場合などに用いられる。抽出操作が簡単な点は長所であるが、偏りのある標本にならないように注意する必要がある。

　次に二段抽出法を説明しよう。大きさNの母集団をk個のグループに分け、各グループの大きさをN₁、N₂、……、N_kとする(N=N₁+……+N_k)。第iグループに確率N_i/Nを与えて、k個のグループのうちの一つのグループを抽出する。次にそのグループの中から大きさnの標本を抽出する。この方法を二段抽出法という。また多段抽出法も考えられている。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

標本調査【ひょうほんちょうさ】

統計調査において，全対象から一部分（標本）を抽出して調査や検査を行い，その結果から全対象について推定すること。全数調査の対。全数調査が不可能なとき（破壊検査など），調査のための費用や時間に制限があるとき等に用いられる。→抽出法
→関連項目大量観察法｜無作為抽出｜乱数表

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

標本調査
ひょうほんちょうさ
sample survey

有限母集団から，研究，調査の目的に合致し，かつ有効な標本抽出の方法を考える統計の分野 (標本調査法) ，または標本による調査そのものをいう。統計の一般論において，たとえば未知の母平均 m ，母分散 σ² の正規分布からの任意標本というとき，その標本をいかに抽出するかについての具体的方法までは言及されない。正確には標本調査では，母集団が有限個数の抽出単位 (抽出操作の基本となる単位) から成るものであればよいので，母集団に含まれる抽出単位の個数 N とすれば，調査計画に基づき各抽出単位に抽出確率が割当てられ，N のなかから大きさ n の標本が抽出される。

出典　ブリタニカ国際大百科事典 小項目事典

流通用語辞典

標本調査【sampling survey】

調査をしようとする集団の全体（母集団という）の中から、一部分をくじ引きの方法で無作為に抽出して調査対象者（標本という）とする調査。母集団全体を調査するには、膨大な時間と経費を要することが多いため、母集団を代表するように科学的なサンプリングによって調査対象者を設定し、その結果から母集団全体について推計する調査方法で、各種の調査に広く用いられている調査方法である。来店客調査などでも、全来店客を調査対象とするのではなく、来店客の一部を抽出して調査し、その結果から来店客全体の動向をつかむ方法がとられている。

出典　(株)ジェリコ・コンサルティング

世界大百科事典（旧版）内の標本調査の言及

【経済統計】より

…経済現象を対象として，統計調査によって得られた結果を数字で表現したものをいう。統計調査には全数調査と標本調査の二つがある。全数調査はセンサスとも呼ばれ，たとえば国勢調査では全国の全世帯，事業所統計では全事業所というように，対象となる客体をすべて網羅している。…

【抽出法】より

…サンプリングともいう。統計調査の対象となる集団からその構成要素の一部分(標本)をとりだして調査に付すいわゆる標本調査において，標本のとり方を抽出法(あるいは標本抽出法)という。抽出法にはいろいろな技法があるが，各構成要素を標本にするか否かを一定の確率法則に従う手段で決める方法を無作為抽出法(あるいは任意抽出法)，確率的には決めない方法を有意抽出法(あるいは有意選択法)という。…

【統計学】より

…数理統計学のなかにはこのような一般理論のほか，一つの対象について同時に多くの観測値が得られる場合のデータを扱う多変量解析法，対象の時間的変化を表すデータを扱う時系列解析法(時系列分析)などが，それぞれ独自の体系を作っている。　統計データの作成法を扱う分野として，標本調査法と実験計画法があげられる。標本調査法は多数の構成単位からなる大きい集団(母集団という)の特性値を，その構成単位の一部(標本という)だけを取り出して観察することにより，推定する方法を取り扱う。…

※「標本調査」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」