大円（読み）ダイエン

デジタル大辞泉

だい‐えん〔‐ヱン〕【大円】

１ 大きな円。
２ 球面を中心を通る平面で切ったときにできる切り口の円。
[類語]丸っこい・丸まっちい・丸丸・丸い・丸まろい・真ん丸・円まろやか・円まどか・円つぶら・円形・球形・球状・輪形・円・同心円・半円・楕だ円・長円・真円・正円・真ん丸い・くりくり・たまご形・ループ・輪わ・輪わっか・リング・丸まる・丸める・丸・団団・団子状

出典　小学館

精選版 日本国語大辞典

だい‐えん‥ヱン【大円】

1. 〘 名詞 〙
2. ① 大きな円形。
3. ② 数学で、球面を、その中心を通る平面で切ったとき、切り口に現われる円。球面を平面で切ってえられる円の中でもっとも大きいものであるところからいう。⇔小円。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
4. ③ 天のこと。
   1. [初出の実例]「天 大円(タイヱン)〈略〉大円は大にして円也(まとかなり)とよむ。円覆はまどかにしておほふ也。いづれも天の形を云也」(出典：邇言便蒙抄（1682）五)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

大円 (だいえん)
great circle

球の中心を通る平面が球面と交わってできる円を大円と呼び，この平面に垂直な球の直径を大円の軸，その両端の点を大円の極という（図）。球面上に大円を一つ定めたとき，この大円を赤道，二つの極を北極，南極と呼び，両方の極を通る大円を子午線と呼ぶことがある。球面上に直径の両端でない2点A，Bがあるとき，これらを通る大円がただ一つ定まり，AとBを端点とする大円の弧のうちの小さいほうは球面上でAとBを結ぶ最短の道となる。
執筆者：中岡 稔

図－大円

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

大円【だいえん】

球面とその中心を通る平面との交わり，一つの球面上に描かれる円の内で最も大きい。大円は球面上の測地線で，球面上の任意の２点を結ぶ曲線のうち，大円の劣弧（半円より小さい弧）が最短。球面とその中心を通らない平面との交わりは小円という。
→関連項目起潮力｜大圏航路

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

大円
だいえん
great circle

球面を，球の中心を通る平面で切った切り口の曲線。球を平面で切った切り口の曲線はすべて円となるが，そのなかで最も大きな円となることから，この名がある。その他の円を小円という。球面上の2点の最短コースは，その2点を通る大円上にある。

出典　ブリタニカ国際大百科事典 小項目事典

最新 地学事典

だいえん
大円

great circle

⇒ ステレオ投影

出典　平凡社「最新 地学事典」

普及版 字通

【大円】たいえん

天。

字通「大」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の大円の言及

【球面三角法】より

…まず，球面三角形について述べよう。球面をその中心を通る平面で切ったときの切口の円を大円great circleといい，球面の一つの直径の両端の2点を対心点antipodal pointという。球面上の2点A,Bが対心点でなければ，A,Bを通る大円の周上においてAをBに結ぶ劣弧を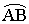で表す。…

【球】より

…球面を平面で切れば切口は円となる。この円を平面が中心を通るときには大円といい，そうでないときには小円という。大円の半径は球の半径に等しく，小円の半径は球の半径より小さい。…

【球面三角法】より

…まず，球面三角形について述べよう。球面をその中心を通る平面で切ったときの切口の円を大円great circleといい，球面の一つの直径の両端の2点を対心点antipodal pointという。球面上の2点A,Bが対心点でなければ，A,Bを通る大円の周上においてAをBに結ぶ劣弧を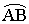で表す。…

※「大円」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」