改訂新版 世界大百科事典 「統計的推定」の意味・わかりやすい解説
統計的推定 (とうけいてきすいてい)
statistical estimation
事物の集合を定量的に把握するための数理統計学の方法を統計的推定という。例えば日本の成人男子の身長とか，ある生産工程で製造される大量の電気抵抗器など，非常に多くの事物の集合を考える。この集合を母集団と呼ぶ。母集団はある工程で今後製造される製品全体というように仮想的に定められることもあるので，一般に要素を全部書き出すことは不可能であり，統計的性質を記述することによってそれにかえる。ふつうは平均μ，分散σ2など少数のパラメーターで記述することが行われる。単峰で対称な集合ならこの二つのパラメーターで母集団分布のだいたいの形がつかめる。
平均μ，分散σ2の母集団から無作為にとったn個の標本x1，……，xnに基づいてμ，σ2を推定する統計的考え方は次のようである。標本平均，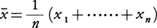
の期待値は母平均μに一致する。これは，各xi（i＝1，……，n）の期待値Eがμであることから，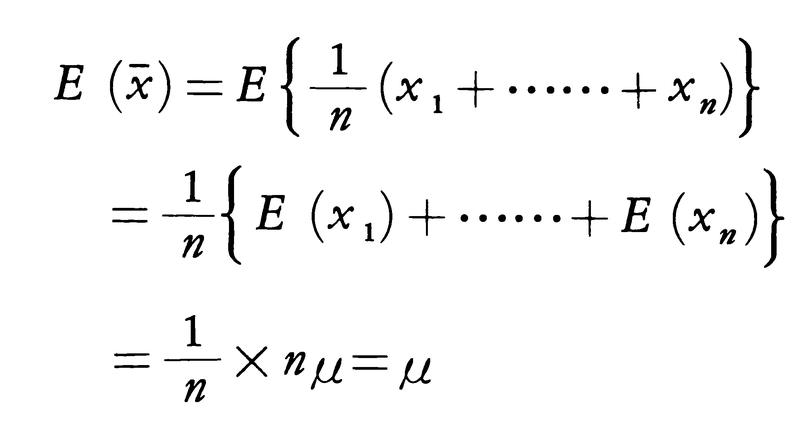
のように知られる。このように期待値が母数と一致するような推定量を不偏推定量と呼ぶ。すなわちxはμの不偏推定量である。不偏性は推定量にとって好ましい性質の一つには違いないが，それだけでは推定量のよさをいったことにならない。例えば，一つ一つのxiもそれぞれμの不偏推定量である。そこでμのまわりのばらつきぐあいを分散で評価する。xの分散Vは各xiが無相関であることから次のように計算される。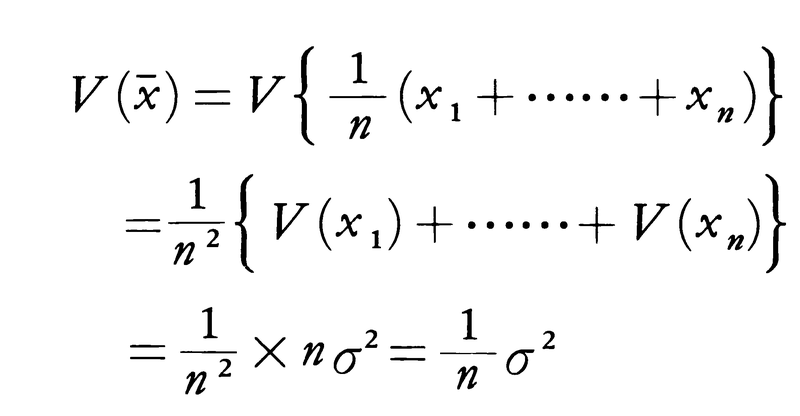
これからxはnを大きくするといくらでもμの近くに集中するような推定量であることがわかる。とくにxi（i＝1，……，n）の線形結合で表されるようなすべての不偏推定量，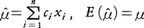
の中でxは分散が最小であることがいえる。このような推定量を線形最小分散不偏推定量（略して線形最良推定量）と呼ぶ。
xは，各xiと期待値μの偏差平方和，
s＝（x1－μ）2＋……＋（xn－μ）2
を最小にするμの値に等しい。これはもっと複雑な問題で，xiの期待値が未知パラメーターμ1，……，μpの線形結合li1μ1＋……＋lipμpで表されているときに偏差平方和，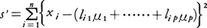
を最小にするような推定方式（最小二乗法）の特別な場合に当たる。最小二乗法による推定量は一般にxiが等分散，無相関のとき線形最良推定量であることが示される。等分散，無相関の仮定が満たされないときは最小二乗法は必ずしもよい推定量を与えない。そのため，これらの仮定からの乖離の影響を受けにくい頑健な推定方式もいろいろ研究されている。
偏差平方和sにおいてμをxで置き換えた統計量，
s＝（x1－x）2＋……＋（xn－x）2
の期待値は，
E（s）＝（n－1）σ2
となることが示される。したがって，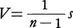
はσ2の不偏推定量になる。Vは自由度n－1の不偏分散と呼ばれる。これはxi－x（i＝1，……，n）を加えると0になり，n次元から一次元縮退していることを表している。
母集団が正規分布N（μ，σ2）に従うときは，xやVについて，より強い最適性がいえる。すなわち，線形に限らずあらゆる推定量の中でxはμの最小分散不偏推定量であり，Vはσ2の最小分散不偏推定量である。
正規分布の密度関数は，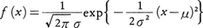
で与えられる。互いに独立なn個の標本の同時密度は，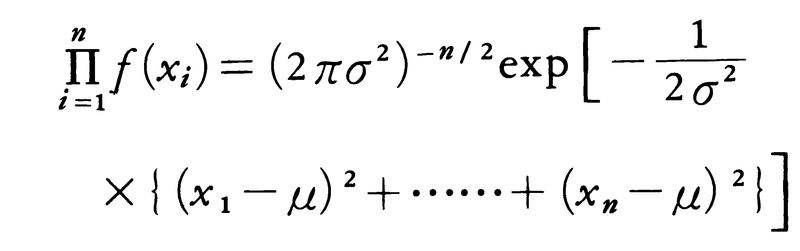
で与えられる。これを未知パラメーターμ，σ2の関数として見たときに尤度（ゆうど）関数L（μ，σ2）と呼ぶ。一般に尤度関数を最大にする母数の値を最尤推定量という。最尤推定量はnが大きいとき漸近的に不偏で，分散が不偏推定量に対する分散の下限を達成し，かつ正規分布に従うような推定量になる。正規分布の場合，最尤推定量は，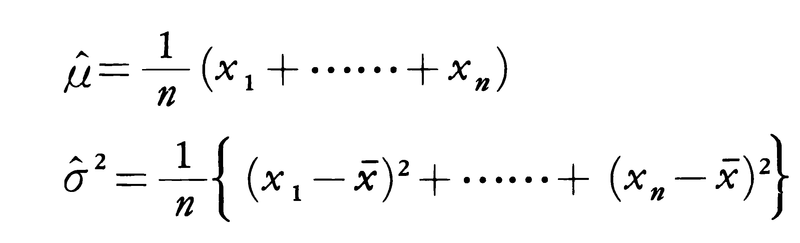
となる。すなわちxは最尤推定量であるが，Vは最尤推定量ではない。
不偏性は推定量のための絶対条件ではない。他の規準，例えば，平均二乗誤差最小規準で推定量を比較することもいろいろ行われている。
以上述べてきた推定方式は未知パラメーターに対し，ただ一つの統計量を対応させる方式であって，点推定と呼ばれる。これに対し，標本から，ある定められた確率で未知パラメーターを含むような区間を構成する方式があり，区間推定と呼ばれる。正規分布からの独立標本x1，……，xnの場合，xが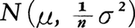
に従うことから，
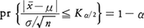が成り立つ（〈統計的検定〉の項参照）。不等式をμについて解くと，信頼率（1－α）の信頼区間，
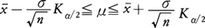が得られる。ここでσが未知で，推定量
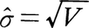を用いる場合にはt分布を用いて次の信頼区間が得られる。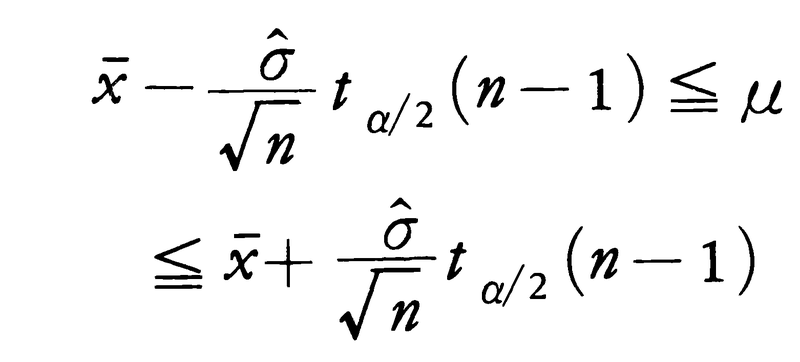
これらの信頼区間は，標本に基づいて100回このような区間を構成すると約100（1－α）回は真の母数を含むという意味あいのものである。αは0.05にとることが多い。
執筆者：広津 千尋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報