H定理
えいちていり
1872年にボルツマンが、気体分子の速度分布が衝突によって不可逆な緩和過程を示すことに関して提出した定理。1分子の位置、運動量をそれぞれr,pとしその分布関数をf(r,p,t)とする。これを用いて関数
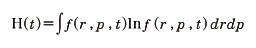
の時間発展を考える。分布関数の時間変化において分子が互いに衝突して速度を変えていく過程を考慮すると、Hは時間の単調減少関数であることが示せる。Hがこれ以上減少しない状態になれば、それが熱平衡の状態であり、そのときのfがマクスウェルの速度分布則になることをボルツマンは示した。彼はこれによって熱現象の不可逆性の原因を説明しようとしたが、力学の可逆性(ロシュミットの逆行性批判)やJ・H・ポアンカレの再帰定理との矛盾(ツェルメロ)など多くの議論を呼び起こした。ボルツマンはそれに対し、H定理を導出するには、分子の衝突に関する力学的考察だけでなく、多数の分子の位置や速度に関する確率的・統計的な処理の導入が不可欠であることを示し、不可逆性は確率的なものであることを明らかにした。いいかえれば、系全体を表す多体系の分布関数は時間反転対称であるのが、一体の分布関数へ縮約する過程での情報の欠落が不可逆性の重要な要素になっている。なおHは系のエントロピーのミクロな表式である情報量的エントロピーに比例する量であり、H定理はエントロピー増大の原理を表している。
[宮下精二]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
H定理【H theorem】
ボルツマンの H 定理*.ハー(H)定理というのはドイツ読みで,現在ではエイチ(H)定理*のほうが普通になっている.
気体の分子が分子的な混乱状態にあるとして,その中で速度の直交成分 u,v,w が u~u+du,v~v+dv,w~w+dw の間に入る分子の数を Fdudvdw で表すとき,u,v,w の可能な全空間における積分をとったものが「ボルツマンの H 関数」で,次の形となる.
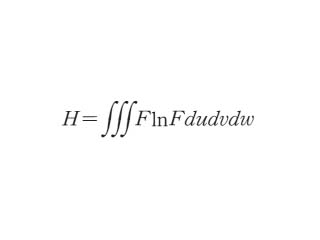
気体の状態が定常であれば dH/dt=0,非定常であれば dH/dt<0となる.つまり F がマクスウェル分布*であれば,H は定数となるが,そうでない場合には H は時間とともに減少してしまう.観点を変えれば,この H 関数はエントロピーをボルツマン定数*で除して符号を変えたものと等しい.
H定理【H theorem】
ボルツマンのH定理*.ドイツ読みにして,ハー(H)定理*と呼ぶこともある.気体の分子が分子的な混乱状態にあるとして,その中で速度の直交成分 u,v,w が u ~ u+du,v ~ v+dv,w ~ w+dw の間に入る分子の数を Fdudvdw で表すとき,u,v,w の可能な全空間における積分をとったものがボルツマンの H 関数で,次の形となる.
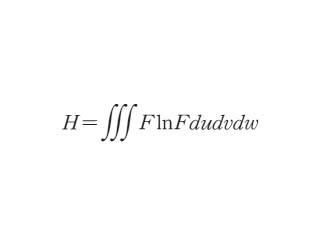
気体の状態が定常であれば dH/dt=0,非定常であれば dH/dt<0となる.つまり F がマクスウェル分布*であれば,H は定数となるが,そうでない場合には H は時間とともに減少してしまう.観点を変えれば,この H 関数はエントロピーをボルツマン定数*で除して符号を変えたものと等しい.
H定理【H theorem】
出典 朝倉書店法則の辞典について 情報
Sponserd by 
H定理
エイチていり
H-theorem
気体分子運動論において,気体分子の位置を r ,運動量を p ,時間を t としてその分布関数を f(r,p,t) とすると,H 関数は次のように定義される。
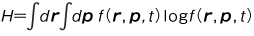 H は時間とともに増大することはなく,dH/dt≦0 であることがボルツマン方程式を用いて証明される。この式をボルツマンの H 定理という。 dH/dt=0 は熱平衡状態に対応し,気体分子はマクスウェル分布になっている。この定理は熱力学第二法則に対応するものである。こうして気体分子の集団を記述する可逆的な運動方程式から,巨視的な不可逆性をもつボルツマン方程式が得られるというパラドックスが説明される。この点の研究は非平衡状態の統計力学の発展に重要な役割を果した。
H は時間とともに増大することはなく,dH/dt≦0 であることがボルツマン方程式を用いて証明される。この式をボルツマンの H 定理という。 dH/dt=0 は熱平衡状態に対応し,気体分子はマクスウェル分布になっている。この定理は熱力学第二法則に対応するものである。こうして気体分子の集団を記述する可逆的な運動方程式から,巨視的な不可逆性をもつボルツマン方程式が得られるというパラドックスが説明される。この点の研究は非平衡状態の統計力学の発展に重要な役割を果した。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
H定理
エッチテイリ
H theorem
L. Boltzmannは気体分子の速度分布則f(v,t)の時間的遷移について,関数,
H(t) = ∫flog f dv3
を導入して議論した.かれは数学的につねに
dH/dt ≦ 0
になることを示し,体系が熱平衡状態にある場合に限り
dH/dt = 0
で,そのときの分布f(v,t)はvに関して正規分布になっていることを示した.これをボルツマンのH定理という.H定理は熱現象における非可逆性を数式的に示すもので,その当時,力学的方程式の可逆性との矛盾に関して議論をよび,多くの研究者によって批判された.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
世界大百科事典(旧版)内のH定理の言及
【統計力学】より
…ボルツマンは第2法則の解析的証明として,極小値がエントロピーに比例する量E=∫……∫flogfdxdydzdvxdvydvzを発見し,気体が固定壁に囲まれているときE(H関数と呼ばれる)は時間とともに減少することを証明した。これをボルツマンのH定理といい,これによりボルツマン自身はエントロピーは増大するという第2法則は証明されたと考えた。ただし,Eはエントロピーとは符号が異なるので,のち,バーバリが文字EをHに変えた。…
※「H定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
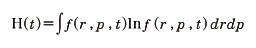


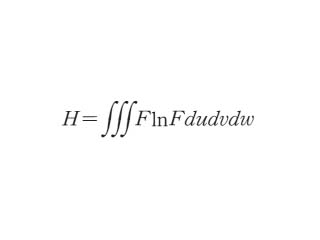
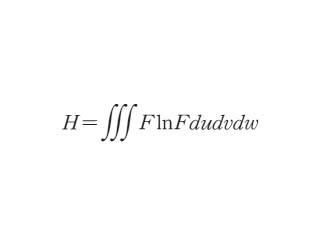
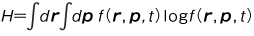 H は時間とともに増大することはなく,dH/dt≦0 であることが
H は時間とともに増大することはなく,dH/dt≦0 であることが