パラドックス（英語表記）paradox

デジタル大辞泉

パラドックス（paradox）

《「パラドクス」とも》「逆説」に同じ。

出典　小学館

精選版 日本国語大辞典

パラドックス

1. 〘 名詞 〙 ( [英語] paradox )
2. ① 一見、不合理であったり矛盾したりしていながら、よく考えると一種の真理であるという事柄。また、それを言い表わしている表現法。逆説。
   1. [初出の実例]「俗人の考ふる全智全能は、時によると無智無能とも解釈が出来る。かう云ふのは明かにパラドックスである」(出典：吾輩は猫である（1905‐06）〈夏目漱石〉五)
3. ② 論理学で、ある命題と、それの否定命題が共に成り立つと結論され、その推論の中に誤りがあることを明確に指摘できない二命題。逆説。
4. ③ 常理に反する説で、その説に反する正当な論拠を見いだしがたいもの。逆説。
   1. [初出の実例]「詭辯はよし給え。つまらんパラドックスは自分で自分を不幸にするやうなものだ」(出典：ふらんす物語（1909）〈永井荷風〉再会)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

パラドックス
paradox

一般に正しいと思われていることに反することがらをいう。〈背理〉〈逆理〉〈逆説〉などともいわれる。語源的には，ギリシア語のpara（超えた，外れた，反した）とdoxa（考え，通念）の合成に由来する。一般に正しいと思われていることがらは必ずしも一定したものではなく，社会や時代によって異なる。したがってある社会でパラドックスと考えられることも別の社会ではパラドックスではない。コペルニクス理論が普及するまでは〈地球は動く〉ということはパラドックスとして扱われたであろう。しかし世に正しいとされていることに反することがらをただ主張するだけではそれは承認されないであろう。そこにはそれを裏付ける議論ないし証拠がなければならない。たとえば，

　1/2円＝5銭　　……（1）　

と主張しても，これを直ちに認める人はいないが，正しい関係式

　1/4円＝25銭　　……（2）　

の両辺を平方に開いてこれを導出したのだといえば，（1）があながち否定できなくなり，急にパラドックスめいて感じられる。もっとも，この議論はまちがっていて（2）の両辺を平方に開いても（1）は成立しないから，これは本当のパラドックスではない擬似パラドックスである。逆に地動説はそれを裏付ける議論や証拠の方が天動説のそれよりも優れていたために，天動説に代わって世に受け入れられ，そのためパラドックスめいたところはなくなってしまったのである。

　こうして多くのパラドックスが当初思われていたようなパラドックスではなく，それは見かけ上のものにすぎないことがわかるから，擬似的だからといってパラドックスでないとするのは適当でない。現に解けていないパラドックスも擬似的なものかもしれない。これに反し，あとで述べる論理的パラドックスはその擬似性を暴露することによって解かれるのではなく，それが述べられる言語を修正し，パラドックスが生じないように定式化しなおすことによって解決されたと考える。これは容易ではないから，擬似性の明白なパラドックスとの差は大きい。しかし議論のあやまりが比較的容易に見いだされるパラドックスであっても，そこにまぎらわしく，また興味深い論点が含まれていれば，パラドックスとして注目されることになる。前述の（2）の両辺を平方に開くことによって（1）を出すのはこの例である。

　パラドックスにはつぎのような各種のものがある。まず経験的事実に関するもの。たとえば，外部からエネルギーを補給しないで永久運動を行う装置－－物理学で第1種の永久機関という－－のモデルをつくれるとするパラドックス，〈シュレーディンガーの猫〉のように，微視的なもののふるまいをモデル化したパラドックスがこれである。もっと概念的なパラドックスには，数量，時間空間，運動，その他の抽象的なカテゴリーに関するもの，論理的パラドックスなどがある。時間・空間に関するパラドックスで有名なのはカントの二律背反である。これは，時間を無限の過去から流れてきたものとすればその反対の有限のものとしなければならなくなり，逆に有限なものとすればかえって無限の過去から流れてきたということになるとするものである。空間を無限の広がりと考えたときも同様である。このように，あることを立てるとちょうどその否定が結果するという形のパラドックスを二律背反という。運動に関するパラドックスの代表的なものにエレアのゼノンのパラドックスがある。これは運動が一般に不可能だとするもので，ゼノンはこれを四つの形で述べた。このなかでとくに，〈飛んでいる矢はとまっている〉〈アキレスは先に出発した亀を追い抜くことができない〉という二つのパラドックスは有名である。一般に哲学に登場するアポリア（難問）は，抽象的なカテゴリーに関するパラドックスの形で述べられることが多い。たとえば，意志の自由と客観世界の決定性とのかかわりは，カントによって二律背反の形で述べられた。

　しかしパラドックスのなかで理論的に一番重要なのは論理的パラドックスである。これは数学の基礎づけおよび（論理的）意味論の構成にかかわり，大きな学問分野を形成させたからである。論理的パラドックスは意味論的パラドックスと集合論ないし論理学のパラドックスとに分けられる。意味論的パラドックスの代表的なものはリシャールのパラドックス，ベリーのパラドックス，グレリングのパラドックス，エピメニデスのパラドックスなどである。それは語や文の定義や真偽，何を指すか，いかなる意味をもつかにかかわる。たとえばグレリングのパラドックスは，述語の意味からあらゆる述語を2種類に分けたときに生ずるパラドックスで，エピメニデスのパラドックスは，クレタ人エピメニデスが〈自分はうそつきだ〉といったというところから，このことばの真偽を考えたときのパラドックスである。このことばの真偽は，どちらをとってもその反対が帰結されるのである。このパラドックスの解決はタルスキーによってもたらされた（1935）が，そのときの理論が機縁になって（論理的）意味論という新しい哲学的領域が形成された。集合論のパラドックスは最大の順序数ないし基数を考えるときにブラリ・フォルティおよびG.カントルのパラドックスとして現れた。B.A.W.ラッセルは，すべての集合を自分自身を元とする第1種の集合と自分自身を元としない第2種の集合との2種類に分けるとき，第2種の集合の全体（これも一つの集合である）をとるとパラドックスが導かれることを見いだした（1901）。つまりこの集合を第1種としても第2種としてもその反対が帰結されるのである。これをラッセルのパラドックスという。これは順序数や基数の概念も必要としない純粋に論理的なパラドックスで，以後の論理学と数学基礎論の発展に大きな影響を与えた。このパラドックスをラッセルはタイプ理論によって解決したが，公理論的集合論を構成してその中に矛盾が生じないようにして解く方法も案出された。
執筆者：中村 秀吉

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

パラドックス
ぱらどっくす
paradox

ある命題とその否定命題が、ともに論理的に同等と思われる論拠をもって主張されているとする。これらの二つの命題が成り立つと結論する推論のなかに誤りが含まれていることを明確に指摘することができないとき、これら二つの命題を、パラドックス、逆理または逆説という。以下にその有名な例をあげる。

　エピメニデスEpimenidesのパラドックス（前6世紀ごろ）は、表現はいろいろあるが、たとえば「クレタ人はうそつきであるとあるクレタ人はいった」という命題をいう。「クレタ人はうそつきである」という小命題が正しければそのクレタ人はうそをいったことになり、小命題がうそであればそのクレタ人はうそをいっていないことになり、いずれにしても全体の命題は成立しない。

　エレアの哲学者ゼノンのパラドックス（前5世紀）は数個あるが、そのなかの二つをあげる。(1)俊足のアキレスがカメを追いかけても、カメに追い付くことはできない。なぜなら、アキレスが元のカメのいた所まできたときには、カメはなにがしか前進している。次にまたアキレスがそのときカメのいた所まできたときには、カメはまたなにがしか前進している。したがって、アキレスはカメに追い付くことはできない。(2)飛んでいる矢は、各瞬間において一定の位置を占める。すなわち、矢は各瞬間においてその位置で静止している。ゆえに矢は運動することができない。

　次は、集合概念についてのパラドックスである。(1)G・カントルのパラドックス（1899）。「Sはすべての集合の集合である」という命題があるとする。Sをすべての集合の集合、TをSの部分集合の全体のつくる集合とすれば、Tの濃度はSの濃度より大きい。同時にT⊂S（TはSの部分集合）であるから、Tの濃度はSの濃度より大きくない。したがって、この命題は成立しない。(2)B・A・W・ラッセルのパラドックス（1903）。「自分自身を元として含まない集合の集合」。自分自身を元として含まない集合の全体のつくる集合をNとする。このとき、N∈Nとすれば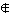NNが、N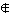NとすればN∈Nが導かれて矛盾がおこる。ここで、a∈A,a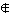Aはそれぞれ、「aは集合Aの元である」「aは集合Aの元でない」を表す。

　また、リチャードJ. A. Richardのパラドックス（1905）も有名で、いろいろあるが、その一つは「100字以内で定義できない最小の自然数」は、現にこの文によって100字以内で定義されているという種類の逆理で、エピメニデスの逆理が伝承されている。

［西村敏男］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

パラドックス
paradox

正当な推論方法に基づきながら，一般に認められている結論とは反対の，あるいは自家撞着する結論にいたる説をいう，論理学用語。逆説，逆理とも訳し，今日では二律背反も含めることが多い。古代ギリシアのエレアのゼノンが提出した「飛ぶ矢は飛ばない」「アキレウスはカメに追いつけない」などのパラドックスは有名（→ゼノンのパラドックス）。主として実存に関する問題を扱う宗教や実存主義哲学（→実存主義）などでは，悟性的記述をこえるため，逆説的な表現によってしか真理が告げられないこともあり，その積極的な意義を肯定しなければならない。たとえば「色即是空」とか「無が存在の根拠」というような文である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

パラドックス

ギリシア語のpara（反，超）＋doxa（意見，通念）の合成に由来する。〈背理〉〈逆理〉〈逆説〉と訳。一般に正しいと考えられていることに反する主張や事態をいう。レトリックとしての逆説的表現もパラドックスに含みうるが，通常はより概念的なもの，たとえばカントの二律背反（アンチノミー），〈ゼノンのパラドックス〉，さらには〈エピメニデス（嘘つき）のパラドックス〉や〈ラッセルのパラドックス〉など論理的なものを指すことが多い。後２者の場合のごとく，パラドックスの解決が新しい学問領域を開く（論理的意味論，タイプ理論）ことも少なくない。
→関連項目詭弁

出典　株式会社平凡社