精選版 日本国語大辞典 「三角形」の意味・読み・例文・類語
さんかっ‐けいサンカク‥【三角形】
日本大百科全書(ニッポニカ) 「三角形」の意味・わかりやすい解説
三角形
さんかくけい
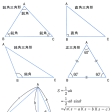
同一直線上にない3点とそれらを結んでできる三つの線分からなる図形。その3点を三角形の頂点といい、三つの線分を三角形の辺という。三角形の二つの辺でできる三つの角を三角形の角といい、3辺、3角を三角形の六要素という。三角形の三つの角の和はどの三角形でも一定で180度である。三角形の2辺の和は第3辺より長く、2辺の差は第3辺より短い。三角形の三つの頂点を通る円を外接円といい、三角形の三つの辺に接する円を内接円という。どの三角形も外接円、内接円がかける。
三角形の六要素、すなわち、3辺3角のうち、(1)2辺とその挟む角を与えれば三角形は定まる。(2)2角を与えれば残りの角も定まり、さらに1辺を定めれば三角形は決定する。(3)線分を三つ与えて、2線分の長さの和がもう一つの線分の長さよりもつねに大きいという条件を満たすなら、3線分を辺とする三角形が決定する。以上の3条件をそれぞれ、辺角辺、角辺角、辺辺辺の決定条件という。
三角形の三つの角がいずれも鋭角のとき鋭角三角形という。三角形の一つの角が直角のとき直角三角形、一つの角が鈍角のとき鈍角三角形という。直角三角形や鈍角三角形では残りの2角はいずれも鋭角である。三角形の2辺が等しいとき二等辺三角形といい、等しい2辺が挟む角を頂角、その対辺を底辺という。二等辺三角形の底辺の両端の角は大きさが等しく、それらを二等辺三角形の底角という。三角形の3辺が等しいとき三つの角も等しくなり、その大きさは60度である。3辺の等しい三角形を正三角形という。直角三角形で直角を挟む2辺が等しい三角形を直角二等辺三角形という。その底角は45度である。また、正三角形の一つの垂線で分けられる直角三角形の二つの角は60度、30度である。直角三角形の直角に対する辺を直角三角形の斜辺という。
三角形の外接円の中心、内接円の中心をそれぞれ三角形の外心、内心という。このほか三角形については特有な点がある。重心、垂心、傍(ぼう)心である。あわせて三角形の五心という。
[柴田敏男]
三角形の面積
三角形の面積を表す公式はいろいろある。1辺の長さがaで、これに対する高さがhの三角形の面積Sは、S=ah/2である。また、2辺の長さa、bの積に、その挟む角θの正弦の2分の1を乗じてもよい。つまり、S=(absinθ)/2である。面積を三角形の3辺で表す公式にヘロンの公式がある。3辺の長さをa、b、cとすれば、三角形の面積Sは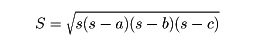
で表される。ここでs=(a+b+c)/2である。
[柴田敏男]
改訂新版 世界大百科事典 「三角形」の意味・わかりやすい解説
三角形 (さんかくけい)
triangle
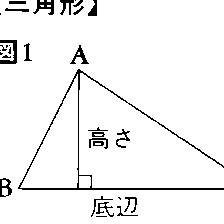
1直線上にない3点A,B,Cがあるとき,三つの線分AB,BC,CAでできる図形を三角形ABCといい,△ABCで表す。A,B,Cをその頂点,BC,CA,ABをその辺という。各頂点に対しその点を含まない辺を対辺という。三角形の頂点からその対辺への距離をその対辺を底辺とみたときの高さという(図1)。△ABCにおいて,∠BACを頂点Aにおける内角または頂角といい,∠Aで表す。これに対し,図2における∠B′ACおよび∠BAC′を頂点Aにおける外角という。頂点B,Cにおける内角および外角も同様に定義される(図2)。三角形の三つの内角の和は2直角である。直角より大きい内角をもつ三角形を鈍角三角形,直角に等しい内角をもつ三角形を直角三角形といい,3内角のいずれもが直角よりも小である三角形を鋭角三角形という。直角三角形において頂角が直角である頂点の対辺を斜辺という(図3)。三角形において,大きい頂角をもつ頂点の対辺は小さい頂角をもつ頂点の対辺よりも大きく,この逆も成り立つ。2辺の長さが等しい三角形ABCを二等辺三角形といい,AB=ACならば∠Aをその頂角,BCをその底辺,∠Bおよび∠Cをその底角という(図4)。二等辺三角形の底角は等しく,またこの逆も成り立つ。すなわち,二つの内角が等しい三角形はこれらの2内角を底角とする二等辺三角形となる。3辺の長さが等しい三角形を正三角形という。正三角形では3内角の大きさは等しく,60度であるが,逆に3内角の大きさが等しい三角形は正三角形となる(図5)。三角形の面積Sは,S=1/2ah,または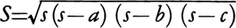 (ヘロンの公式)で与えられる。ここにaは1辺の長さで,hはこの辺を底辺とみたときの高さを表し,a,b,cは三角形の3辺の長さで,s=(a+b+c)/2である(図6)。三角形に対し,次の(1)~(5)に述べる3直線をつくるとき,いずれの場合もそれら3直線は1点で交わる。(1)三つの内角のおのおのを2等分する直線,(2)一つの内角と他の二つの外角のおのおのを2等分する直線,(3)各頂点を対辺の2等分点に結ぶ線分(これを中線という),(4)各頂点を通り対辺に垂直な直線,(5)各辺を垂直に2等分する直線。(1)~(5)における3直線の交点をそれぞれ三角形の内心,傍心,重心,垂心,外心といい,これらを総称して三角形の五心という(図7)。二つの三角形において,次の(1)(2)(3)のいずれかが成り立つとき,これら二つの三角形は合同となる。すなわち,一方の三角形を動かして他の三角形の上に重ね合わすことができる。(1)3辺の長さが等しい,(2)2辺とその間の角が等しい,(3)1辺とその両端の角が等しい。この事実を三角形の合同定理と呼んでいる。
(ヘロンの公式)で与えられる。ここにaは1辺の長さで,hはこの辺を底辺とみたときの高さを表し,a,b,cは三角形の3辺の長さで,s=(a+b+c)/2である(図6)。三角形に対し,次の(1)~(5)に述べる3直線をつくるとき,いずれの場合もそれら3直線は1点で交わる。(1)三つの内角のおのおのを2等分する直線,(2)一つの内角と他の二つの外角のおのおのを2等分する直線,(3)各頂点を対辺の2等分点に結ぶ線分(これを中線という),(4)各頂点を通り対辺に垂直な直線,(5)各辺を垂直に2等分する直線。(1)~(5)における3直線の交点をそれぞれ三角形の内心,傍心,重心,垂心,外心といい,これらを総称して三角形の五心という(図7)。二つの三角形において,次の(1)(2)(3)のいずれかが成り立つとき,これら二つの三角形は合同となる。すなわち,一方の三角形を動かして他の三角形の上に重ね合わすことができる。(1)3辺の長さが等しい,(2)2辺とその間の角が等しい,(3)1辺とその両端の角が等しい。この事実を三角形の合同定理と呼んでいる。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「三角形」の意味・わかりやすい解説
三角形【さんかくけい】
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の三角形の言及
【ヤントラ】より
… 図形としては,次のようなものが用いられる。点(それ以上凝縮しえない究極的相を示す),直線(成長・展開の相を示す),円(〈全体〉を表す),四角形(自然の質料を表す),三角形(サーンキヤ学派の説く純質・激質・暗質という自然の三つの性質などを示し,下向きのものは女性原理を,上向きのものは男性原理を表す),下向きと上向きの二つの三角形が交わってできる六芒星の形(六角の星形で,現象世界を顕現させる力を表す),五芒星(地・水・火・風・空の〈五大〉などを表す)などである。そのほかに〈門〉を表す形(聖域に入る入口を示す),蓮の花弁の形(神格の属性としての願望を成就させる力などを表す)なども用いられる。…
【三角定規】より
…直角三角形の他の二つの角を,45度,または30度と60度とした板状の定規。以前はセルロイド製,木製のものが用いられたが,最近ではほとんど透明アクリル板製のものが使用されている。三角定規の大きさは,45度定規の斜辺と30度‐60度定規の対辺が同じ長さにつくられており(図1),ふつう2枚1組になっている。この2枚およびT定規,または固定定規を組み合わせることにより,図2のように15度,30度,45度,60度,75度,90度の傾斜線を引くことができる。…
【トライアングル】より
…打楽器の一種。鉄を主とした直径8~12mm,長さ45~75cmの金属円棒を三角形に折り曲げたもの。通常,紐でつり下げ同種の細い金属棒で奏する。高い響きを有する。打つ位置・角度により音色が変わる。奏法,使用法は奏者の創意による。19世紀まで底辺に3個から5個の円い鉄の輪がはめられていた。トルコの軍楽隊からヨーロッパの軍隊に導入され,東洋情緒の描写にオーケストラで使われるようになった。リストは《ピアノ協奏曲第1番》でソロとして使用している。…
※「三角形」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...