ポテンシャル論（読み）ポテンシャルろん（英語表記）potential theory

改訂新版　世界大百科事典

ポテンシャル論 (ポテンシャルろん)
potential theory

ベクトル場FがスカラーUによってF＝－gradUと表されるとき，UをFのポテンシャルという。

　例えば，三次元空間の，集合Eを占める物体Mがあり，点Q∈Eにおける密度がρ（Q）のとき，万有引力の定数をGとおけば，物体Mによる重力の場Fは，ポテンシャル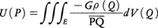，の－grad Uに等しい。

　P＝P（x，y，z）とすると，この関数はポアソンの方程式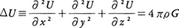，をみたす。したがって，とくに，Eの外点では⊿U＝0をみたしている。つまり調和関数である。

　ポテンシャル論は，もとは物理学の一部であったが，19世紀になって，S.ポアソン，G.グリーン，C.ガウスらによって数学の対象として理論が作られ始めた。とくにガウスの功績は大きい。

　ポテンシャル論の対象の一つとして，ディリクレ問題Dirichlet problemがある。これは，与えられた領域で調和で，境界で与えられた関数と一致するものを求める問題である。この問題の解は，適当な質量を用いた積分で表すことができる。例えば，原点O中心で半径がRの球においては，その表面S上に与えられた連続な境界値をfとしたとき，ディリクレ問題の解は，次のポアソン積分によって与えられる。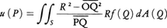　現在では，一般の空間Xの測度μとX×Xの関数K（x，y）が与えられたときに決まる関数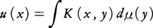，のことを〈Kを核としμを質量分布とするポテンシャル〉と呼び，このような関数に関連した理論をポテンシャル論という。Xが三次元ユークリッド空間のとき，K（x，y）＝｜x－y｜⁻¹を核とするものをニュートンポテンシャルNewton potentialという（dμ＝－GρdVとしたものがちょうど前述のものである）。二次元ユークリッド空間では，

　K（x，y）＝－log｜x－y｜

を核とする対数ポテンシャルが重要である。じっさい，これは，質量の分布されてないところでは，平面での調和関数であるので，関数論との関連が深い。なお，一般のポテンシャル論は，確率論とも密接な関係がある。
執筆者：及川 廣太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ポテンシャル論
ぽてんしゃるろん
theory of potential

とし、関数u(x,y,z)=-1／rを考えると、原点にある質量1の質点と、(x,y,z)にある質量1の質点の間の引力は、ベクトル

で表される。このとき、関数u(x,y,z)を重力場Fのポテンシャルという。

　このように、ベクトル場F(x,y,z)が、関数u(x,y,z)により

の形で表されるとき、u(x,y,z)をF(x,y,z)のポテンシャルという。

　　F(x,y,z)
　　　=(f(x,y,z),g(x,y,z),
　　　　h(x,y,z))
がポテンシャルをもつ必要十分条件は
　　rotF=0すなわち、

である。

［洲之内治男］

[参照項目] | ベクトル解析

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ポテンシャル論
ポテンシャルろん
potential theory

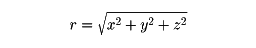
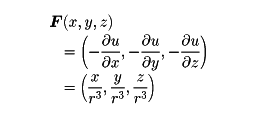
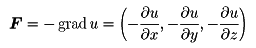
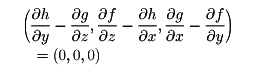
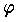力学で，ベクトル量の力 F の代りにスカラー量のポテンシャル を考えれば，力は 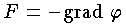，すなわち，力の成分は 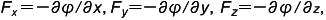で与えられる。静電場 E や静磁場 H に対しても同様な電気ポテンシャル (電位) ，磁気ポテンシャル (磁位) が考えられる。ポテンシャル 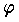は物質 (または電荷，磁荷) が体積密度 ρ で分布するところ，および分布しないところで，それぞれ次の式を満足する。
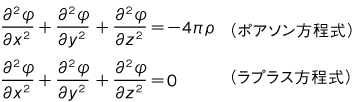物質 (電荷，磁荷) の分布が既知のとき，これらの偏微分方程式の境界値問題の解としてポテンシャル 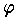を求め，力場 (電場，磁場) を定めるなど，ポテンシャルに関する数学をポテンシャル論という。

出典　ブリタニカ国際大百科事典 小項目事典