翻訳|tensor
精選版 日本国語大辞典 「テンソル」の意味・読み・例文・類語
テンソル
日本大百科全書(ニッポニカ) 「テンソル」の意味・わかりやすい解説
テンソル
てんそる
tensor
ベクトルの考え方を拡張したもので、数学、とくに幾何学や、物理学で重要な働きをする概念。張力tensionに由来することば。ベクトル・行列・内積といえば、代表的な基本的概念である。これらは、本来別々に生まれた概念であるが、以下述べるようにひとたびテンソルという概念を導入すると、同じ仲間として統一的に取り扱えるのである。
まず実数の全体をRで表し、VをR上のn次元ベクトル空間とする(n次元ユークリッド空間RnはVの代表例である)。rを自然数とする。TをVのr個の直積V×…×VからRへの写像とする。すなわち、Vのr個の元X1,…,Xrを決めるたびに実数T(X1,…,Xr)がただ一つ定められているとする。このとき、番号i(=1,…,r)とVの元X1,…,Xi-1,Xi+1,…,Xrを固定しておくと、Vの元Xを決めるたびにRの元
T(X1,…,Xi-1,X,Xi+1,…,Xr)
がただ一つ定まる。すなわちVからRへの写像が得られたことになる。それがすべての番号iとすべてのVの元X1,…,Xi-1,Xi+1,…,Xrに対して線形になっているとき、TをV上のr次テンソルという。
V上のr次テンソルTは次のようにして数量的に表記できる。Vに一つの基{e1,…,en}を定めておくと、Vの元はすべてx1e1+…+xnen(x1,…,xnはRの元)の形で一通りに表せる。r×n個の実数をxij(i=1,…,r;j=1,…,n)で表し、添え字i1,…,irは1からnまで動くものとすると、テンソルの定義から次が得られる。
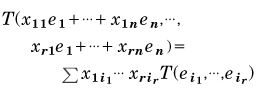
ここで、Σはi1,…,irについて和をとるものする。この式はテンソルTはnr個の実数の組{T(i1,…,ir)}で決まってしまうことを意味している。そこで、その組を基{e1,…,en}に関するTの成分という。
〔例1〕V上の1次テンソルの全体はVの双対空間V*にほかならない。また、V*上の1次テンソルの全体はVとみなせることが知られている。
〔例2〕TをV上の2次テンソルとする。Vの一つの基に関するTの成分はn2個の実数からなっている。したがって、Vに一つ基を定めるたびに、V上の2次テンソルの全体と2次実正方行列の全体の間に1対1の対応があることがわかる。また、V上の(正定値)内積とは、V上の2次テンソルTで、次を満たすもののことである。
(1)Vのすべての元XとYに対してT(X,Y)=T(Y,X)かつT(X,X)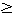 0
0
(2)X≠0ならT(X,X)>0
とくに、Rnの2元X=(x1,…,xn)とY=(y1,…,yn)に対してT0(X,Y)=x1y1+…+xnynとおけば、T0はRn上の内積である。これをRnの標準的内積という。
〔例3〕X1,…,XnをRnの任意の元とする。i=1,…,nに対して、Xi=(xi1,…,xin)とおく。xij(i,j=1,…,n)を成分とするn次正方行列をXで表して、T(X1,…,Xn)=detXとおけば、TはRn上のn次テンソルであることがわかる。
[高木亮一]
物理学におけるテンソル量
質点の位置ベクトルrの成分(x,y,z)は座標系のとり方により値が異なる。直角座標系の3軸を、原点を通るある軸の周りに、ある角度回転させて新しい座標系に移させると、質点の座標(x,y,z)は別の値(x',y',z')に変化する。x、y、zのかわりにx1、x2、x3と書くと、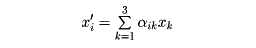
なる線形の関係で位置ベクトルの成分の間の変換が表される。αikは定数で、座標系の回転の仕方で定まる。
質点の速度Vの成分もまったく同じ変換をする。rと同一の変換を、座標系の回転に対して行う量を1階のテンソルまたはベクトルとよぶ。質点の位置、速度、加速度などは1階のテンソルである。二つの1階テンソルA、Bがあるとき、9個の成分をもち、その成分がAiBj(i、jは、1、2、3のいずれかの値をとる)である量を考え、2階のテンソルという。また一般にAiBjと同一の変換を座標系の回転に対して行う9個の成分をもつ量Tijがあるとき、Tijを2階のテンソルという。とくにTij=Tjiのとき2階の対称テンソルという。独立な成分は6個である。またTij=-Tjiのとき2階の反対称テンソルという。独立な成分は3個になる。質点の角運動量は2階の反対称テンソルの例である。位置ベクトルrの大きさの平方r2は座標系の回転により変わらぬ量で零階のテンソルまたはスカラーとよぶ。この種の量として電荷、質量などがある。一般にn個のベクトルの積のように変換するn階のテンソルを考えることができる。
ニュートンの運動法則は運動量の時間変化が力に等しいとしたものであるが、この両者は1階のテンソル(ベクトル)であり、座標系を回転しても同じように変換するので、直角座標系の軸のとり方によらずに成立する。一般に物理学の基礎法則は同じ階数の異なるテンソル量を等しいと置いたもので、座標軸のとり方によらずに成立する。
[武田 暁]
改訂新版 世界大百科事典 「テンソル」の意味・わかりやすい解説
テンソル
tensor
テンソルの概念はベクトルの概念を拡張したものであって,それを含むものである。テンソルの語源は弾性変形の応力(その一種である張力tension)にちなんでいる。すなわち密度一様な球状弾性体に一方向の張力を作用させると,変形して楕円体,
Σaijxixj=c
(xi,xjは三次元空間の座標,cは定数)
となり,9個の係数aijが一つのテンソル成分となるが,これは応力そのものがテンソル量であることによるのである。
n次元ベクトル空間Eに1組の基底ei(i=1,……,n)を固定すると,Eのベクトルv=Σvieiは,上に一つの添字をもつn個の実数vi(i=1,……,n)の組として取り扱える。これと同じ流儀でいえば負でない整数r,sに対して,r次反変,s次共変テンソル,または(r,s)テンソルは上にr個,下にs個の添字をもつnr⁺s個の実数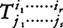 (1≦ik,jl≦n)の組であるということができる。例えば,ベクトルviは一次反変テンソルである。ここで,下につけた添字はEの上の線形関数,すなわち余ベクトルをeiの双対基底eiを用いて下に添字をつけたn個の実数wj(j=1,……,n)の組として表す場合のように,双対であることを示すものである。これを一次反変テンソルviが一つの余ベクトルwj上で,また一次共変テンソルwjが一つのベクトルvi上で値Σviwiをとるものと解釈すれば,r次反変s次共変テンソル
(1≦ik,jl≦n)の組であるということができる。例えば,ベクトルviは一次反変テンソルである。ここで,下につけた添字はEの上の線形関数,すなわち余ベクトルをeiの双対基底eiを用いて下に添字をつけたn個の実数wj(j=1,……,n)の組として表す場合のように,双対であることを示すものである。これを一次反変テンソルviが一つの余ベクトルwj上で,また一次共変テンソルwjが一つのベクトルvi上で値Σviwiをとるものと解釈すれば,r次反変s次共変テンソル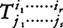 はr個のベクトルとs個の余ベクトルに対して値をとる,例えば,二次共変テンソルTi, jは2個のベクトルui,viに対して値
はr個のベクトルとs個の余ベクトルに対して値をとる,例えば,二次共変テンソルTi, jは2個のベクトルui,viに対して値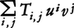 をとるものと考えることができる。この値のとり方は各ベクトルに対して線形であるので,逆に,r個のベクトルとs個の余ベクトルに対して定められた各成分について線形な写像Tをテンソルと定義することも行われる。この場合,先に与えたテンソルの定義における
をとるものと考えることができる。この値のとり方は各ベクトルに対して線形であるので,逆に,r個のベクトルとs個の余ベクトルに対して定められた各成分について線形な写像Tをテンソルと定義することも行われる。この場合,先に与えたテンソルの定義における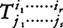 はTが基底ベクトル
はTが基底ベクトル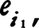
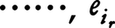 と双対基底ベクトル
と双対基底ベクトル 上でとる値にほかならない。このことからもわかるように,テンソルを
上でとる値にほかならない。このことからもわかるように,テンソルを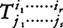 によって表現するときは,その見かけが基底系の選び方によって変わることに注意しなければならない。二次共変テンソルTの例でいうと,それを基底系eおよびēiによって表したものを,それぞれ
によって表現するときは,その見かけが基底系の選び方によって変わることに注意しなければならない。二次共変テンソルTの例でいうと,それを基底系eおよびēiによって表したものを,それぞれ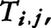
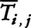 とかけば,
とかけば,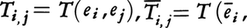
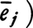 であるから,
であるから,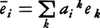 とするとき,
とするとき,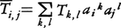 であることになる。以上のテンソルは,線形代数におけるテンソルであり,それを考えるベクトル空間Eは一つに固定されていたが,微分可能多様体の幾何学で現れるテンソルは,多くの場合,接点pによって変動する接ベクトル空間E(p)上で定められるものであって,したがって接点pによって変動するE(p)上のテンソルT(p)が考えられねばならない。微分可能多様体の点pのまわりで,局所座標系(xi(p))をとってみると,それはpおよびpのまわりの点qでの接ベクトル空間E(p)およびE(q)の基底系∂/∂xiを自然に定めている。そこで,かりに点pのまわりの各点qでE(q)上の二次共変テンソルT(q)を考えるものとすると,これは,局所座標系(xi(p))によって,
であることになる。以上のテンソルは,線形代数におけるテンソルであり,それを考えるベクトル空間Eは一つに固定されていたが,微分可能多様体の幾何学で現れるテンソルは,多くの場合,接点pによって変動する接ベクトル空間E(p)上で定められるものであって,したがって接点pによって変動するE(p)上のテンソルT(p)が考えられねばならない。微分可能多様体の点pのまわりで,局所座標系(xi(p))をとってみると,それはpおよびpのまわりの点qでの接ベクトル空間E(p)およびE(q)の基底系∂/∂xiを自然に定めている。そこで,かりに点pのまわりの各点qでE(q)上の二次共変テンソルT(q)を考えるものとすると,これは,局所座標系(xi(p))によって,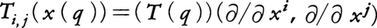 と表現され,さらに(xi(p))以外にもpのまわりの局所座標系(yi(p))が与えられるときは,基底系∂/∂xiが基底系∂/∂yiによって,
と表現され,さらに(xi(p))以外にもpのまわりの局所座標系(yi(p))が与えられるときは,基底系∂/∂xiが基底系∂/∂yiによって,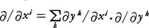 と表されることから,
と表されることから,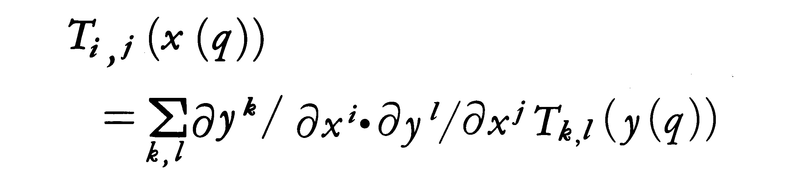
なる等式が成立するはずであることがわかる。逆に,微分可能多様体の各局所座標系(xi(p))で与えられた実数の組Ti, j(x(p))が上の等式をみたすとき,これは二次共変テンソルを与えるといえる。このような座標による表現の利点は,与えられたテンソルの連続性,微分可能性を判定しやすい点にもある。すなわち,それらは各表現が点の関数とみて連続,または微分可能であるものとすればよいからである。なお,単にテンソルというときは,少なくとも連続性が,そして多くは,適当な微分可能性が仮定されているのが通常である。
執筆者:四方 義啓
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「テンソル」の意味・わかりやすい解説
テンソル
→関連項目スカラー
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「テンソル」の意味・わかりやすい解説
テンソル
tensor
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内のテンソルの言及
【スピノル】より
…電子のように1/2のスピンをもつ状態,さらに一般に任意のスピンをもつ状態を表すために導入された量で,スピノルの名もスピンに由来している。三次元空間を回転させたとき,その中の量は回転に伴って変化するが,その変化のしかたによってスカラー,ベクトル,テンソルなどに区別される。変化しないものをスカラーといい,空間内の変位を表す矢印と同じようにふるまうのがベクトルであり,数個のベクトルの積と同じように変化するのが高階のテンソルである。…
※「テンソル」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

