ハミルトニアン
Hamiltonian
古典力学を正準形式に書き表すために導入された量であるが,量子力学においてきわめて重要な役割を果たす。
古典力学のハミルトニアン
古典力学で質点系を一般化座標qiで表し,運動エネルギーをK,ポテンシャルエネルギーをVとする。L(qi,qi)=K-Vからpi=∂L/∂qiを定義し,piをqiに共役な運動量という(qiの・は,qiの1階の時間微分の意味)。qiをqiとpiで書き表し,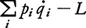 をqiとpiの関数として表したH(qi,pi)をこの力学系のハミルトン関数,あるいはハミルトニアンと呼ぶ。Kがqiの二次斉次式のときはHは系の全エネルギーに等しく,ハミルトニアンは系の全エネルギーを座標と運動量で書き表したものである。運動方程式は,
をqiとpiの関数として表したH(qi,pi)をこの力学系のハミルトン関数,あるいはハミルトニアンと呼ぶ。Kがqiの二次斉次式のときはHは系の全エネルギーに等しく,ハミルトニアンは系の全エネルギーを座標と運動量で書き表したものである。運動方程式は,
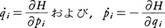
の形のハミルトンの方程式で与えられる。これは1階の方程式であり,ニュートンの方程式に比べて広い対称性をもち,数学的に取扱うときに便利である。
→解析力学
量子力学のハミルトニアン
量子力学においても同じ表式H(qi,pi)を用いる。ただしqi,piは量子力学的な非可換量であり,Hは線形空間の要素に作用するエルミート演算子となる。このHをハミルトニアン演算子,あるいは単にハミルトニアンという。状態を表す波動関数ψの時間的変化はシュレーディンガー方程式,
iℏψ=Hψ
によって与えられる(ħは,プランク定数を2πで割ったもの)。座標qiとしてデカルト座標xiを用いるならば,ハミルトニアンは,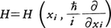 で与えられる。Hは系のエネルギーに対応する量(演算子)であり,その固有値E1,E2,……は系のエネルギー準位を与える。
で与えられる。Hは系のエネルギーに対応する量(演算子)であり,その固有値E1,E2,……は系のエネルギー準位を与える。
執筆者:宮沢 弘成
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ハミルトニアン
はみるとにあん
Hamiltonian
粒子や場のシステムのエネルギーを座標と運動量で表現したもの、および量子力学におけるエネルギー演算子をいう。後者はハミルトン演算子ともいわれる。ここで座標qは、対象としているシステムの運動を表すことができる限り任意に選んでよいが、運動量pはこれに応じて定まってくる。このような座標と運動量が特別の関係を有することをイギリスのW・R・ハミルトンがみいだした。この関係を正準共役(きょうやく)、この場合の座標と運動量を正準共役な力学変数という。先に述べたハミルトニアンとは、正準共役な力学変数でエネルギーを表現したものをハミルトンの名にちなんでよんでいるものである。したがって単振動を行う質量mの質点のハミルトニアンは(1/2m)p2+(1/2)Kq2(Kは力の定数)であるが、これを(m/2)(dq/dt)2+(K/2)q2と書けばハミルトニアンではない。
[田中 一]
量子力学ではqとpとを演算子と考え、この間にqp-pq=-iħの関係が成り立つと考えている。p=-iħ∂/∂qはこの関係の具体的な一つの表現である。この結果、量子力学のハミルトニアンは古典力学のハミルトニアンのpを-iħ∂/∂qで置き換えた演算子Hとなり、量子力学の運動状態、すなわち量子的状態 の時間的変化はiħ∂
の時間的変化はiħ∂ /∂t=H
/∂t=H で与えられる。
で与えられる。
[田中 一]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ハミルトニアン
ハミルトニアン
Hamiltonian
ハミルトン演算子ともいう.保存力の場のなかを動く粒子については,運動エネルギーTと位置のエネルギーVの和は一定である.いま,Vは一般化位置座標 qi だけの関数とし,Tを qi とそれに共役な一般化運動量 pi で表し,
T(q1,q2,…,qi,…;p1,p2,…,pi,…)
とする.
T(…,qi,…;…,pi,…) + V(…,qi,…) = H(…,qi,…;…,pi,…)
をハミルトニアンという.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
ハミルトニアン
Hamiltonian
古典力学におけるハミルトン関数をさすこともあるが,通常は量子力学において系の全エネルギーに対応する演算子をさし,ハミルトン演算子ともいう。 ps を一般運動量,qs を一般座標,また s=1,2,…,N ( N は自由度の数) としてハミルトン関数を H(ps,qs) で表わし,ps,qs に対応する量子力学的演算子を代入するとハミルトニアンになる。ハミルトニアンは,量子力学において基本的に重要な役割を果している。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
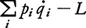 をqiとpiの関数として表したH(qi,pi)をこの力学系のハミルトン関数,あるいはハミルトニアンと呼ぶ。Kがqiの二次斉次式のときはHは系の全エネルギーに等しく,ハミルトニアンは系の全エネルギーを座標と運動量で書き表したものである。運動方程式は,
をqiとpiの関数として表したH(qi,pi)をこの力学系のハミルトン関数,あるいはハミルトニアンと呼ぶ。Kがqiの二次斉次式のときはHは系の全エネルギーに等しく,ハミルトニアンは系の全エネルギーを座標と運動量で書き表したものである。運動方程式は,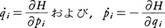
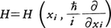 で与えられる。Hは系のエネルギーに対応する量(演算子)であり,その固有値E1,E2,……は系のエネルギー準位を与える。
で与えられる。Hは系のエネルギーに対応する量(演算子)であり,その固有値E1,E2,……は系のエネルギー準位を与える。

 の時間的変化はiħ∂
の時間的変化はiħ∂