ホモロジー（読み）ほもろじー（英語表記）homology

デジタル大辞泉

ホモロジー（homology）

異種の生物間に成り立つ形態的に等しい構造関係。例として、鳥の翼とコウモリの翼手があげられる。相同。相同性。

出典　小学館

日本大百科全書(ニッポニカ)

ホモロジー
ほもろじー
homology

ホモロジーは、ホモトピー理論と並んで、組合せおよび代数的トポロジーにおける基本概念である。

多面体

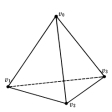
n次元空間Rⁿにあるr+1個の点v₀,v₁,……,v_rが一般の位置にあるとは、どのs個(s≦r)の点もs-一次元部分空間上にないことである。これらの点v₀,v₁,……,v_rを含む最小の凸集合をr‐単体という。

　一点v₀は0単体、線分|v₀v₁|は1単体、三角形|v₀v₁v₂|は2単体、四面体|v₀v₁v₂v₃|は3単体である（図）。一般のr‐単体は|v₀v₁……v_r|で示される。ここでv₀,v₁,……,v_rをその頂点とよぶ。

　　σ^r=|v₀v₁……v_r|のとき、そのs+1個の頂点で定まるs‐単体σ^sをσ^rの辺単体という。また、次の二つの条件を満たす単体の集合Kを複体という。

（1）σ∈Kならばσの辺単体はすべてKに属す。

（2）σ,σ′∈Kならば、σ⊃σ′はσおよびσ′の共通の辺単体である。

　Kに属す単体の最大次元をそのKの次元という。Kの単体の和集合を多面体といい|K|で示す。

　Rⁿの部分集合Xは、|K|=Xとなるような複体Kが存在するとき、三角形分割されるという。

［野口　廣］

ホモロジー群

複体Kが与えられているとする。Kの各単体σ^r=|v₀v₁……v_r|にその向きを考える。向きは頂点の順列であり、偶置換で移れる向きは同じとし、そうでない向きは異なる向きとしてマイナスをつけて区別する。向きをつけた単体は、その順列の順に頂点を並べてσ^r=＜v₀v₁……v_r＞と示す。以下単体は向きをつけられているものとする。これらr‐単体の整数を係数とした和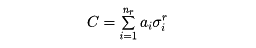

をr‐鎖という。r‐鎖の集合はr‐単体を基とする自由加群C_r(K)をつくる。各r‐単体σ^rにその境界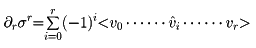

を定める。ここで＜v₀……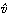_i……v_r＞はv_iを除くことを示す。この境界∂_rσ^rはr-1鎖であり、この対応を線形に拡大して準同形写像
　　∂_r:C_r(K)→C_r-1(K)
を得る。∂_r-1゜∂_r=0であることが示されるので、
　　∂_r+1(C_r+1(K))⊂Ker∂_r
よって剰余加群
　　Hr(K)=Ker∂_r/∂_r+1(C_r+1(K))
が定まり、これをKのr次元ホモロジー群という。H_r(K)は、位相空間Xの三角形分割によらずに一定するので、これをH_r(X)で示し、Xのr次元ホモロジー群という。

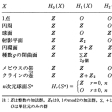
　表1はいろいろな位相空間のホモロジー群を示したものである。

［野口　廣］

ベッチ数・オイラー数

多面体Xのr次元ホモロジー群H_r(X)は有限生成な可換群であり、可換群の基本定理により定まるその階数をXのr次元ベッチ数といい、p_rで示すことにする。そしてこれらの次のような和
　　χ(X)=p₀-p₁+p₂-……+(-1)ⁿp_n
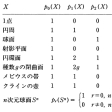
を多面体Xのオイラー数という。表2は、それぞれの多面体のベッチ数とオイラー数を示したものである。

　多面体Xの任意の三角形分割をKとし、Kのr‐単体の個数をα_rで示すと、次のオイラー‐ポアンカレの公式が成り立つ。

　　Σ(-1)^rα_r=Σ(-1)^rp_r=
　χ(X):オイラー数
とくにXが球面であると、p₀=p₂=1,p₁=0であるから
　　α₀　　-　　α₁　　+　　α₂
(頂点の数)(辺の数)(面の数)
　　=p₀-p₁+p₂=2
となり、これがオイラーの多面体公式である。

［野口　廣］

コホモロジー群

複体Kのr‐鎖群をC_r(K)とする。ただし係数は実数とする。このとき、C_r(K)は実数を係数とする線形空間となる。その双対空間をC^r(K)とする。

任意の∈C^r(K)とC∈C_r+1(K)に対して
　　∂^*()(C)=(∂C)
によりコホモロジー境界準同型写像
　　∂^*_r-1:C^r-1(K)→C_r(K)
を定めると、ホモロジー群の場合と同様に
　　∂^*_r゜∂^*_r-1=0
であり、剰余群
　　H^r(K)=Ker∂^*_r/∂^*_r-1(C^r-1(K))が定まり、これが空間X=|K|のr次元コホモロジー群で、ホモトピーの研究に用いられる。

［野口　廣］

[参照項目] | ホモトピー

ホモロジー〔図〕

位相空間のホモロジー群〔表1〕

多面体のベッチ数とオイラー数〔表2〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ホモロジー
homology

位相幾何学の研究法に，図形などの幾何学的対象に群や環などの代数的対象を対応させ，幾何学的性質を代数的性質に反映させて調べるという方法がある。ホモロジーの概念はこの方法の端緒をなしたもので，H.ポアンカレによって始められた。ホモロジーは各位相空間Xに可換群の列H_n（X）（n＝0，1，2，……）を対応させ，連続写像f：X→Yに準同型の列f_*：H_n（X）→H_n（Y）を対応させる。ホモロジーを定義する方法はいろいろあるが，次に特異ホモロジーと呼ばれている方法を述べよう。n次元ユークリッド空間の原点をP₀で，第i座標軸上の単位点をP_iで表し，P₀，P₁，……，P_nを頂点とする単体を△ⁿで表す。また，各i＝0，1，……，nに対し，ε：△ⁿ⁻¹→△ⁿは△ⁿ⁻¹の頂点P₀，P₁，……，P_n-1を△ⁿの頂点P₀，……，P_i-1，P_i+1，……，P_nにこの順序でうつす線形写像を表すとする（図）。さて，位相空間Xに対し，△ⁿからXへ連続写像全体を考え，これらのおのおのをXの特異n単体といい，これらの有限形式和g₁σ₁＋g₂σ₂＋……＋g_rσ_r（ここにg_iは整数で，σ_iはXの特異n単体）をXのn鎖という。Xのn鎖全体は加法により可換群をつくる。これをC_n（X）で表す。各特異n単体σ：△ⁿ→Xに対し（n－1）鎖σ◦ε₀－σ◦ε₁＋σ◦ε₂＋……＋（－1）ⁿσ◦ε_nを対応させることにより，C_n（X）からC_n-1（X）への準同型が得られるが，これを∂_nで表す。このとき，∂_n◦∂_n+1はC_n+1（X）をC_n-1（X）の0にうつすことが示されるから，∂_n：C_n（X）→C_n-1（X）で0にうつるC_n（X）の元全体のつくる部分群をZ_n（X）で表し，∂_n+1：C_n+1（X）→C_n（X）の像である部分群をB_n（X）で表せば，B_n（X）はZ_n（X）の部分群となる。いま，剰余群Z_n（X）/B_n（X）をH_n（X）で表して，Xのn次ホモロジー群という。連続写像f：X→Yがあるとき，Xの特異n単体σ：△ⁿ→Xに対し，Yの特異n単体f◦σ：△ⁿ→Yを対応させることにより，C_n（X）からC_n（Y）への準同型が得られるが，これをf♯で表すとき，f♯はZ_n（X）をZ_n（Y）に，B_n（X）をB_n（Y）にうつすことがわかるから，f♯によりH_n（X）からH_n（Y）への準同型が得られる。これがf_*：H_n（X）→H_n（Y）である。f，f′：X→Yが同じホモトピー類に属するならばf_*＝f_*′で，XとYが同じホモトピー型であればH_n（X）とH_n（Y）は同型な群である。二つの閉曲面が同相となるのはそれらのホモロジー群が同型であるときで，しかもそのときに限る。
執筆者：中岡 稔

図－ホモロジー

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

ホモロジー
ホモロジー
homology

厳密には，共通の祖先に由来する生物や遺伝子を比較するときの用語であるが，単なる類似性の意味でも使われている．

出典　森北出版「化学辞典（第2版）」