対数関数（読み）タイスウカンスウ（英語表記）logarithmic function

デジタル大辞泉

たいすう‐かんすう〔‐クワンスウ〕【対数関数】

aを1でない正の数とするとき、xを正の数として、y＝log_axで定められる関数。指数関数の逆関数。

出典　小学館

精選版 日本国語大辞典

たいすう‐かんすう‥クヮンスウ【対数関数・対数函カン数】

1. 〘 名詞 〙 数学で、初等関数の一つ。正数ｘに、ａを底とするその対数 log_ax を対応させる関数 y=log_ax を、ａを底とする対数関数という。これは、ａを底とする指数関数 y=a^x の逆関数と一致する。単に対数関数といえば、底がｅ（=2.1718…）である自然対数をさすことが多い。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

対数関数 (たいすうかんすう)
logarithmic function

aを1でない正の定数とするとき，任意の正数xに対してa^y＝xとなる実数yがただ一つ定まる。このyを，aを底（てい）とするxの対数と呼んでy＝log_axと書き，xにlog_axを対応させる関数をaを底とする対数関数という。対数関数y＝log_axはaを底とする指数関数y＝a^xの逆関数である。

　対数関数の導関数を求めるため，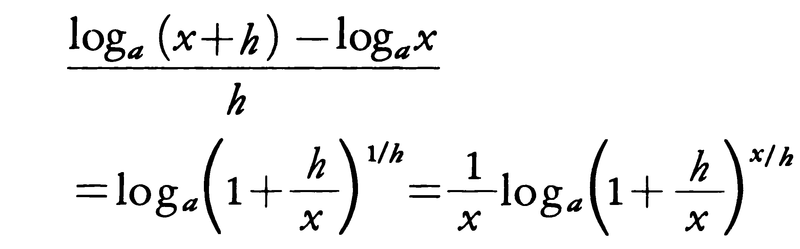

と変形する。ここでx/h＝tとおくと，上の式は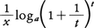，となり，x＞0だからh→±0のときt→±∞（複号同順）となるが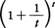，はt→＋∞としてもt→－∞としても同じ定数に近づくことが示される。その値をeで表す。eは無理数であって，

　e＝2.718281828459……

である。eを用いると上の計算から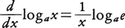，であるから，対数の底としてeを採用すれば，

となってつごうがよい。eを底とする対数を自然対数と呼ぶ。数学の理論においては，単に対数関数といえばeを底とするものを指し，底eを省略してlogxと書く。このとき，一般の正数a≠1を底とする対数関数はlog_ax＝logx/logaとなる。以下，すべてeを底とする対数関数について述べる。

　実変数の関数としての対数関数は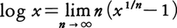，によって定義してもよい。これはx＞0を定義域とし，xの狭義単調増加関数であって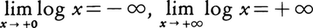，となる。また（1）により不定積分の公式，
　　（積分定数は省略，以下同様）

が得られるが，このほか，初等的な不定積分の公式で対数関数が現れる例として，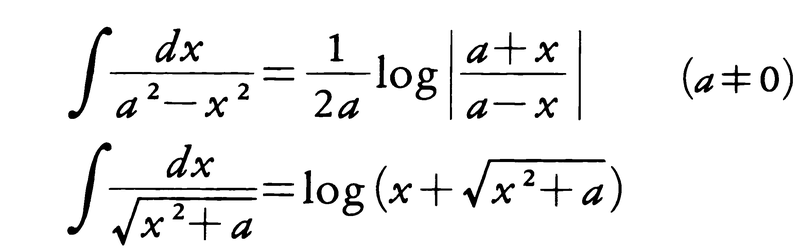

をあげておこう。また一般に関数f（x）が連続な導関数f′（x）をもてば，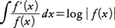

例えば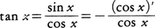，だから，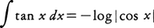

（2）とlog1＝0とから次のlogxの積分表示を得る。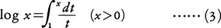

そこで，複素変数zの対数関数logzを，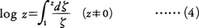

によって定義する。（4）においてzが正の実数の場合には，積分路を複素平面上で1からzまで0をまわらないで到達するように選べば，右辺の積分の値は（3）の右辺と同じになるから，このlogzの定義は実変数x＞0の関数logxの拡張になっている。（4）において，積分路が0のまわりを正の向きに一周するごとに，積分の値が2πi（iは虚数単位）だけ変化し，負の向きに一周すれば－2πiだけ変化する。だから複素変数の関数logzは無限多価関数である。z＝1において0になるその分枝は次のように｜z－1｜＜1において収束する，べき級数に展開される。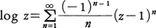

複素数の極形式を用いると，

　z＝re^iθ＝r（cosθ＋isinθ）　（r＞0）

に対して，

　logz＝logr＋iθ　　　……（5）　

となる。θをθ＋2nπ（n＝±1，±2，……）としてもzは変わらないが，（5）の右辺は2nπiだけ変化する。このこともlogzの多価性の反映である。また対数関数については，2πiの整数倍の差を無視することにより，等式，

　log（z₁z₂）＝logz₁＋logz₂

が成り立つ。これは指数関数の満たす等式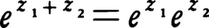に対応するものである。

　対数関数は，代数関数や指数関数とともに初等関数を構成する要素である。三角関数が指数関数を用いて表されるのと同様に，逆三角関数は累乗根（代数関数の一種）と対数関数とを用いて表される。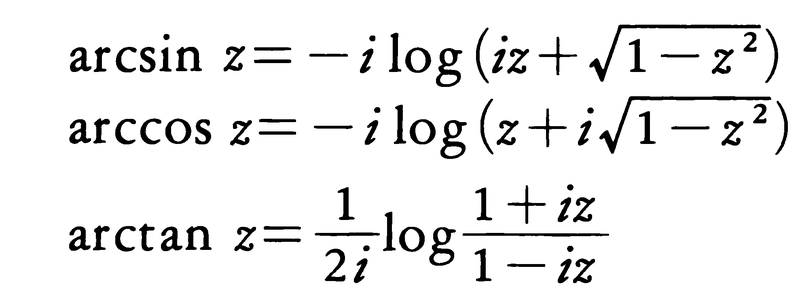


→指数関数　→対数
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

対数関数
たいすうかんすう

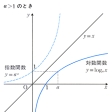
変数xにその対数の値を対応させる関数のこと。a(a＞0,a≠1)を底とする対数関数をy=log_axで表す。y=log_axとはx=a^yのことだから、対数関数は指数関数の逆関数である。y=log_axのグラフは、y=_axのグラフを、直線y=xを軸として折り返せば得られる。log_axは、すべての正の実数xについて定義された関数で、log_a1=0である。a＞1のときは増加関数で、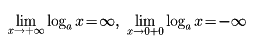

0＜a＜1のときは減少関数で、

対数関数について、次の公式が成り立つ。

　　log_axy=log_ax+log_ay
　　log_ax^k=klog_ax
　　log_ab・log_bc=log_ac
　a=10、すなわち10を底とする対数を常用対数という。対数の底として10を使うのはわれわれが十進(じっしん)記数法を採用していることによる便宜的なものであり、数学的な根拠があるわけではない。数学では、数eを用いるのが普通である。とくに微分積分法との関連においては、諸公式を簡明にするので自然である。すなわち、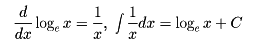

となる。eを底とする対数を自然対数といい、数学では、単にlogxと書けば、eを底とする対数を意味する。これを、自然対数をラテン語で書いたlogarithmus naturalisを略した形でlog nat、あるいはlnと書くこともある。たとえばln(1+x)はlog_e(1+x)を意味する。

　対数関数の値を計算するとき、次の展開式を利用する。

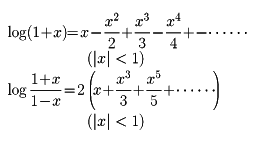
たとえばlog2は第二の式でx=1/3とすれば求められる。

　常用対数は、スコットランドのネーピアによって1615年ころにみいだされ、その後イングランドのブリッグズによって改良され、一般に用いられるようになった。ケプラーはネーピアからの知らせに驚喜してこれを活用し、有名なケプラーの法則の発見に至る計算をしたという。一方、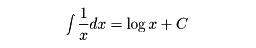

という関係は、1650年ころ、ベルギーのサン・バンサンGregorius Saint Vincent（1584―1667）によってその端緒が得られ、17世紀を通じて、だいたい確立された。

［竹之内脩］

[参照項目] | 関数 | ケプラー | 自然対数 | 対数 | ネーピア | ブリッグズ

対数関数のグラフ

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

対数関数
たいすうかんすう
logarithmic function

a ( a＞0 ，a≠1 ) を底とする x の対数 y ，x＝a^y すなわち y＝ log _ax を x と y の間の関数関係と考えたとき，y を a を底とする x の対数関数という。対数関数 y＝ log _ax は指数関数 y＝a^x の逆関数であり，0＜x＜＋∞ で定義された連続かつ狭義の単調関数である。ただし a＞1 のときは単調増加関数，1＞a＞0 のときは単調減少関数である。

出典　ブリタニカ国際大百科事典 小項目事典