信号検出理論（読み）しんごうけんしゅつりろん（その他表記）signal detection theory

最新 心理学事典

しんごうけんしゅつりろん
信号検出理論
signal detection theory

信号検出理論とは，ノイズの中から信号を検出する際の検出者の反応を定量化する理論である。略称はSDT。1950年代に工学者が開発し，タナーTanner,W.P.とスウェッツSwets,J.A.が心理学の分野に導入した。現在の感覚・知覚実験の土台を支えている重要な理論である。観察者内外で発生しているノイズの存在下で，観察者は刺激を観察し，その結果として観察者内部の心理的連続体psychological continuum（感覚量が表わされる心理的座標軸）に生じる確率変数の値に応じて，刺激中に信号が含まれるか否かについて判断を下す。たとえば光覚閾を測定する際，検出すべき光を信号と考え，光の大小に対応する生体活動の強度が1次元の軸上に値をもつと仮定して，これを心理的連続体と考えよう。たとえ信号が存在しなくても生体活動はなんらかの値Ψをもち，ノイズだけが存在する条件（Ｎ条件）では，Ψは心理的連続体上で確率密度関数Ｘ^N（Ψ）に従い確率分布する。簡単にするため，Ｘ^N（Ψ）は平均0，分散1の正規分布とする。ノイズに加えて信号が含まれる条件（SN条件）では，Ψは確率密度関数Ｘ^SN（Ψ）に従い分布する。等分散モデルにおいて，Ｘ^SN（Ψ）は平均ｄ′，分散1の正規分布と考える（図1）。観察者が信号を検出する事態は，Ｎ条件においてはＸ^N（Ψ）分布から，またはSN条件においてはＸ^SN（Ψ）分布から無作為に選ばれた標本Ψを得たとき，その値のみをよりどころにして「信号あり（ｙ）」または「信号なし（ｎ）」のいずれかをもって反応するという課題だとみなせる。

　心理的連続体上の特定の値ｃを観察者の判断基準criterionとし，Ψ≧ｃであればｙ反応，Ψ＜ｃであればｎ反応をすると考える。すると，信号が存在するSN条件で「信号あり」とｙ反応をするヒット率hit rate，すなわちＰ^H＝Ｐ（ｙ｜SN）は，Ｘ^SN（Ψ）のうちｃより右の面積に等しい。信号が存在しないＮ条件で「信号あり」とｙ反応をしてしまう誤警報率false alarm rate，すなわちＰ^FA＝Ｐ（ｙ｜Ｎ）は，Ｘ^N（Ψ）のうちｃより右の面積に等しい。SN条件でｎ反応をするミス率miss rate，すなわちＰ^M＝Ｐ（ｎ｜SN）は，1－Ｐ^Hに等しい。Ｎ条件でｎ反応をする正棄却率correct rejection rate，すなわちＰ^CR＝Ｐ（ｎ｜Ｎ）は，1－Ｐ^FAに等しい。これらの関係から，二つの分布の平均間の距離はｄ′＝Ｚ（Ｐ^H）－Ｚ（Ｐ^FA）として求められる（ここでのＺ（Ｐ）は累積標準正規分布の逆関数）。したがって，ｄ′とは，信号の有無によって確率分布の平均がどの程度異なるかを，分布の標準偏差を単位として記述するもので，検出力指標detectability indexとよばれる（図1）。

　判断基準ｃは観察者の内的基準（ｙ反応をするに当たり判断がどのくらい慎重か）を反映するほか，報酬価など（たとえば，誤警報に罰を与えずヒットに高報酬を与えつづける操作は，ｃを下げる方向に働く）で変化する。しかし，ｃとｄ′は互いに独立であるため，信号検出理論では信号に対する感度と観察者の判断基準とを独立に記述することができる。さて，Ｘ^N（Ψ）とＸ^SN（Ψ）の確率密度の比ｌ（Ψ）＝Ｘ^SN（Ψ）/Ｘ^N（Ψ）を信号検出理論における尤度比likelihood ratioというが，ｌ（Ψ）＝1に対応するΨの値，すなわち二つの確率密度関数の交点に対応する横軸上の値は，信号が存在しないＮ条件と存在するSN条件において同確率で生じる。Ψがこれより大きければ信号が存在する確率の方が高く，小さければ信号が存在しない確率の方が高い。よって，判断基準ｃをこの値に設定すれば最適な検出ができる。等分散モデルにおいて，β＝l（ｃ）＝Ｘ^SN（ｃ）/Ｘ^N（ｃ）は観察者の判断基準がこの最適な方略からどの程度隔たるかを記述するもので，バイアスbiasの一つの指標であり，ｃ＝ｄ′/2のときβ＝1となり，尤度比が1で，正答率が最大となる。この位置から実際のｃがどれだけ隔たっているかを示す値C＝c－d′/2は，Ｃ＝－1/2［Ｚ（Ｐ^H）＋Ｚ（Ｐ^FA）］として求められ，ｄ′と独立に計算できるバイアス指標としてよく利用される。また，logβ＝d′×Ｃの関係がある。

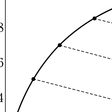
　ある値のｄ′に対し，判断基準がさまざまに変化したときに（Ｐ^FA，Ｐ^H）の点が2次元座標上で変化する様子を表わしたのがROC曲線receiver operating characteristic curveである（図2）。等分散モデルに従うデータならば，ROC曲線は（1,0）と（0,1）を結ぶ対角線に対して線対称となり，対角線と曲線の交点においてｃ＝ｄ′/2であり，正答率が最大となる。実測データがこの形状に沿わない場合，不等分散モデルを導入する必要が考えられる。不等分散モデルにおける検出力指標やバイアスの取り扱いに関しても精緻な理論がある。信号検出理論では，ここに述べた典型的なyes/no法による検出課題以外にも，強制選択法や対象同定法などさまざまな課題に対する適用方法が理論化されている。　→閾　→視覚刺激　→精神物理学　→精神物理学的測定法


〔村上 郁也〕

図2 d'=1.0のときの判断基準cの…

図1 信号検出理論の等分散モデル

出典　最新 心理学事典

ブリタニカ国際大百科事典 小項目事典

信号検出理論
しんごうけんしゅつりろん
signal detection theory

心理学において，雑音のなかから合図 signalの音が聞えるか否かの決定をなす過程を説明する理論。人間のもつ検出力を，態度・動機などの要因から分離して，統計や確率分布による数値で表現する。 1950年代以降，J.A.スウェッツらによって展開され，精神物理学的測定法の一つとして活用されている。

出典　ブリタニカ国際大百科事典 小項目事典