原子価結合法（読み）げんしかけつごうほう（英語表記）valence bond method

改訂新版　世界大百科事典

原子価結合法 (げんしかけつごうほう)
valence bond method

化学結合の機構を説明するための理論の一つ。原子内にあって化学結合にあずかる電子は価電子といわれるが，一般に原子または分子内の電子の挙動は粒子性と波動性の二つの性質をもっている。電子のこのような波動性は波動関数によって説明される。1927年，ハイトラーWalter Heitler（1904-81）とロンドンFritz London（1900-54）は，波動関数を用いて水素分子の結合機構を明らかにした。これが原子価結合法と呼ばれるもので，VB法と略称される。その後この理論はスレーターJohn Clarke Slater（1900-76）やL.C.ポーリングにより多原子分子にも拡張されたので，彼らの名前の頭文字をとってHLSP法とも呼ばれている。この理論では，分子内の価電子は個々の原子に固有な原子軌道に属している状態に近いものと考えられるので，この理論は原子軌道法atomic orbital method，略してAO法とも呼ばれている。これに対し，分子軌道法（MO法）では，価電子は個々の原子軌道から離れて，分子全体に広がる分子軌道に属していると考えることから出発している。

　VB法で水素分子の結合機構を説明すると，つぎのようになる。二つの水素原子（AおよびBと名づける）は基底状態にあり，たがいに無限に遠く離れているとすれば，電子1（二つの価電子の一つを1，他を2と名づける）が水素原子Aの1s軌道にあり，電子2が水素原子Bの1s軌道にある状態（この状態を表す波動関数をφ₁とする）と，逆に電子1がBにあり，電子2がAにある状態（波動関数φ₂）のいずれかにあるはずである。これらの波動関数は，それぞれの1s原子軌道関数を用いて，φ₁＝χ_A（1）χ_B（2），φ₂＝χ_A（2）χ_B（1）で表される。電子1と2は本来区別できないもので，二つの原子が近づいて分子を形成する状態では，分子の波動関数はこれらの波動関数の一次結合で近似できるものと考える。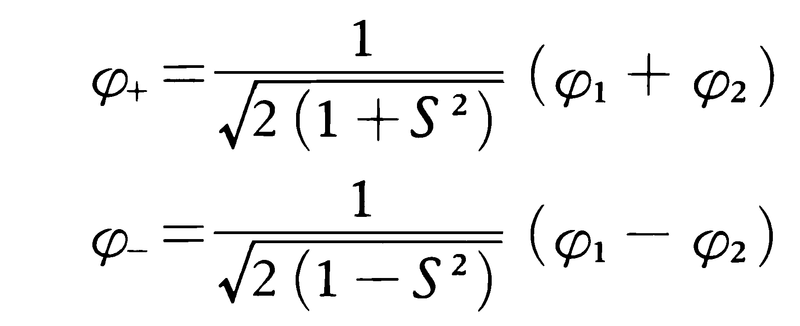

φ₊は電子の位置座標の交換に関し対称な関数，φ_-は反対称な関数である。〈パウリの原理〉に合うように分子の全波動関数ψをつくるには，φ₊にスピン座標の交換に関し反対称であるようなスピン関数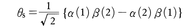を掛け合わせ，φ_-には対称なスピン関数を掛け合わせなければならず，これにより全波動関数ψ_S＝φ₊θ_S，およびψ_Tが得られる。ここにα（1）β（2）は，電子1のスピン状態がα，電子2のスピン状態がβであることを表すスピン関数である。φ₊と組み合わせたスピン関数θ_Sは二つの電子スピンがたがいに逆向きである状態を表しており，これは一重項状態である。これに対し，φ_-と組み合わせたスピン関数は二つの電子スピンが同じ方向を向いている状態を表していて，それは三重項状態である。

　全波動関数がψ_Sおよびψ_Tである状態のエネルギーW_SおよびW_Tを水素分子に対するハミルトニアンHを用いて計算すると，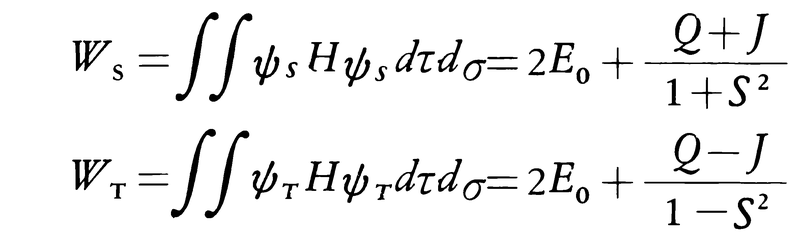

となる。ここに2E₀は水素原子2個分のエネルギーであり，Qはクーロン積分，Jは交換積分，Sは重なり積分である。QもJも核間距離Rの関数であり，Rとして水素分子の実測値0.741Åを用いて計算すると，QおよびJとも負の値となり，R＝0.863ÅでW_Sは極小値を示す。すなわち，この結合機構によりW_Sは2E₀より小さくなり安定な分子が形成されることが説明できたのである。しかし，W_Sから求まる解離エネルギーの値は実測値よりいくぶん小さい。そこでさらに近似を高めるためには，分子の波動関数をつくる際にφ₁＋φ₂の状態（共有結合状態）のほかに，二つの電子がともに水素原子Aに属する状態:χ_A（1）χ_A（2），あるいはBに属する状態:χ_B（1）χ_B（2），すなわち電子が一方に偏っているイオン状態を多少考慮してやればよい。このように共有，イオンなどの構造を混ぜ合わせることを構造間の共鳴という。一方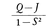，はつねに正の値で，W_Tは極小値をもたず，ψ_Tで表される状態は不安定である。
執筆者：佐野 瑞香

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

原子価結合法
げんしかけつごうほう
valence bond method

原子軌道関数法，または略して VB法ともいう。量子力学的に共有結合エネルギーを求めるための近似計算法の1つ。 1927年 W.ハイトラー，F.ロンドンにより水素分子のエネルギー計算に初めて適用された。分子量子力学の取扱いにはこのほかに分子軌道法 (MO法) がある。分子の電子状態を示す波動関数を組立てるのに，原子価結合法ではまず個々の原子を出発点として，次に原子間相互作用を考えるのに対し，分子軌道法は結合している原子核全体に分布する軌道を考えるところにその特徴がある。

出典　ブリタニカ国際大百科事典 小項目事典

化学辞典 第2版

原子価結合法
ゲンシカケツゴウホウ
valence-bond method

分子の電子状態を表す近似法の一つ．原子軌道(関数)法，または略称してVB法ともいう．ハイトラー-ロンドンの理論がその基礎になっている．すなわち，この理論での特徴は，それぞれ1個の価電子を有する2個の原子が，結合(電子対結合)をつくって分子を形成するときは，価電子は原子に属しているときの状態を保ちながら相互作用を及ぼしあい，かつ交換しあって安定な状態になる，と考えるところにある．この考えを多原子分子の状態を論じる場合に拡張したものが原子価結合法である．

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内の原子価結合法の言及

【化学結合】より

…この場合の共鳴エネルギーは交換エネルギーと呼ばれている。この理論は，化学者の経験から導かれた原子価の概念や分子構造式との対応がよく，原子価結合法として発展した。　この原子価結合法に対してもう一つの理論として，電子は分子全体に広がる軌道(分子軌道)の上を運動するとして扱う分子軌道法がその後導入された。…

※「原子価結合法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」