量子（読み）リョウシ

デジタル大辞泉

りょう‐し〔リヤウ‐〕【量子】

《quantum》一定の最小単位の整数倍という不連続な値をとる物理量の、その最小単位量。プランクの量子仮説で提唱され、エネルギー量子とよばれたが、のちアインシュタインらにより普遍的に適用できることがわかった。クォンタム。

出典　小学館

精選版 日本国語大辞典

りょう‐しリャウ‥【量子】

1. 〘 名詞 〙 光における光量子、あるいは電気量における電気素量のように、ある量がある一定の単位量の整数倍の値で表わされるときに、その単位量のことをいう。
   1. [初出の実例]「光は結局素量的であって、即ち光の元子である。その波の量子エネルギーを定める振動数は」(出典：ルクレチウスと科学（1929）〈寺田寅彦〉二)

出典　精選版 日本国語大辞典

化学辞典 第2版

量子
リョウシ
quantum

M. Planck(プランク)は，かれが提出した黒体の放射法則を量子という革命的な基本的観念を導入することにより，理論的に説明できることを示した．一般に熱放射の源は物体のなかに電荷をもった振動子があり，熱平衡を保ちながらその振動数と同じ振動数の電磁波とそれに伴うエネルギーを吸収したり放出したりしていると考えられる．そして，古典物理学では，その振動子のエネルギーεは統計力学的に温度Tに対応した分布をもつ0から∞までの連続的な値をとるのが当然であるとされていた．しかし，Planckはこのεの値は連続的ではなく，ある定数hと振動数νとの積hνの整数倍：ε ＝ 0，hν，2hν，3hν，…の値のみをとると仮定した．これによって電磁気学と統計力学にもとづいた計算を行うと，放射強度E(T,λ)が波長

λ ＝ c/ν (ただし，cは光速度)
と温度Tにより，

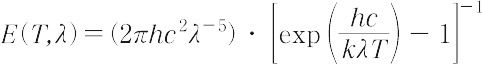
となり，かれの提出した実験式と同じ形になることを示した．ここに，kはボルツマン定数である．このように，原子・分子の極微の世界にあっては，物理量はそれまでの古典物理学で考えていたような連続的なものでなく，ある条件のもとに定まるとびとびの特定の値をとる．これをエネルギーの量子性という．Planckは振動子のエネルギーに対して量子性があることを示したが，その後，1905年にA. Einstein(アインシュタイン)は光電効果の理論で光のエネルギーにも量子性があることを示した．これを光量子という．また1913年にN. Bohr(ボーア)は水素原子のスペクトルの理論において，原子内での原子の運動における角運動量にも量子性があることを一つの条件として見事な成果をおさめた．その後，この量子論はさらに発展して，現在の量子力学という大きな体系がつくりあげられるようになった．[別用語参照]プランクの放射法則，量子条件，量子数

出典　森北出版「化学辞典（第2版）」

日本大百科全書(ニッポニカ)

量子
りょうし
quantum

振動数νの光のエネルギーはhν（hはプランク定数）の整数倍で与えられる。この場合のように物理量の値が基礎量の整数倍で与えられる場合その基礎量を量子という。また電磁場に対する光子、中間子場に対する中間子のように、場を量子化したときに現れる粒子を量子ということがある。

　古典論では一般に物理量が連続的な値をとるものと考えられてきた。量子の発見は古典論から量子力学への移行における決定的な事件であって、量子力学の名称にもこのことが端的に示されている。

　プランクは、空洞内の放射の分布を正しく与えるためには光を放射し吸収する際の原子の振動子のエネルギーが連続的でなくhνの整数倍の値に限る必要のあることを示した。またアインシュタインは、光のエネルギーがhνの整数倍であると考えて、初めて光の吸収によって電子を放出する現象、すなわち光電効果を理解できることを示した。これらはいずれも、エネルギーの量子仮説が、古典論では理解不可能な現象に新しい理解を与えうることを示している。

　ボーアは彼の原子模型のなかで水素原子内電子の定常状態を規定する条件としてボーアの量子条件を与えたが、この条件は電子の作用すなわち運動量をその座標について運動の一周期にわたって積分した量がプランク定数の整数倍であるという形をとっている。

［田中　一］

[参照項目] | アインシュタイン | プランク | プランク定数 | ボーア | 量子化 | 量子条件 | 量子力学

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

量子 (りょうし)
quantum

Aなる量が，ある単位量の整数倍の値しかとり得ないとき，その単位量をAの量子という。たとえば，光は量子的な構成をもち，振動数がνならエネルギーの量子はhν，運動量の量子はhν/cである。ここにhはプランクの定数，cは光速度である。プランク定数が作用量子とも呼ばれるのは，量子力学の前身である古典量子論において，量子条件を〈作用量積分がhの整数倍〉とした歴史による。振動数νの放射のエネルギーをhνの整数倍としたのはプランクの放射則の含意をさぐったM.プランク自身であるが（1900），hνを量子と呼んだのは1909年のプランクからH.A.ローレンツへの手紙が最初である。それ以前にも，量子という語は，電気素量をさして電気の量子といい，またhを作用量子というなどの場合に使われていた。
→作用量
執筆者：江沢 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

量子【りょうし】

ある物理量にそれ以上分割できない最小の単位があり，すべてそれの整数倍として表されるとき，この最小単位をその物理量の量子という。エネルギー量子，光量子（電磁波のエネルギー量子，光子），作用量子（プランク定数）等がある。量子論が生まれる前はエネルギーは無限に分割できる連続量と信じられ，したがって量子の存在は考えられなかった。
→関連項目プランク｜量子条件

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

量子
りょうし
quantum

ある物理量が連続値をとらず，ある単位量の整数倍で表わされる不連続値しかとることができない場合，この単位量を量子という。 M.プランクが導入したエネルギー量子が最初の例である。電気量における電気素量も量子の1つである。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の量子の言及

【場の量子論】より

…一方，弦の振動，水面の波動，物質中の音波などは非相対論的な場の例である。　量子論によればすべての現象は量子化されている。古典場も量子化という手続が必要であり，これが場の量子論である。…

※「量子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」