ルベーグ
Henri Lebesgue
生没年:1875-1941
フランスの数学者。ボーベイに生まれ,エコール・ノルマル・シュペリウールに学び,1920年パリ大学教授,21年コレージュ・ド・フランス教授,翌年アカデミー・デ・シアンス会員に選ばれた。1902年に発表された論文は《積分,長さ,面積》と題し,これらの概念を自然な着想で精密に分析し,それまでのリーマン積分を今日,ルベーグ積分と呼ばれているものに発展させた。これはニュートン,ライプニッツ以来の微分積分法を,項別微分定理,項別積分定理および二重積分と反復積分との同等性を保証するフビニの定理などによって,微積分を自在に駆使できるようにしたもので,その功績は真に大きい。ルベーグ積分の出現は,20世紀のいわゆる実関数論の成立を促し,フーリエ級数論,ポテンシャル論などすべてその影響を受けた。他に位相幾何学,解析学全般で重要な多くの業績がある。
執筆者:吉田 耕作
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ルベーグ
るべーぐ
Henri Lebesgue
(1875―1941)
フランスの数学者。ボーベに生まれ、高等師範学校(エコール・ノルマル・シュペリュール)とパリ大学に学んだ。レンヌおよびポアチエの大学で講師を務め(1902~1910)、パリ大学教授を経て、1921年コレージュ・ド・フランス教授となる。1922年科学アカデミー会員となる。1902年、「積分・長さおよび面積」と題する学位論文において、「完全加法的測度」に基づく可測関数の積分論を創始、それ以前のリーマン積分の本質的な拡張であるばかりでなく、微分と積分とが互いに逆演算であることを明確に示した。これは、「項別微分定理」や「項別積分定理」、また二重積分を反復積分で計算し、反復積分の順序交換をすることの可能性を保証する「フビニFubiniの定理」など微積分を自在に駆使するための理論を与え、ニュートンとライプニッツに始まる微分積分法を現代的にした。
[吉田耕作]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ルベーグ
Lebesgue, Henri Léon
[生]1875.6.28. ボーベー
[没]1941.7.26. パリ
フランスの数学者。エコール・ノルマル・シュペリュール (高等師範学校) で教育を受け,1902年学位を得た。レンヌ大学で助手をつとめ,ポアティエ大学講師 (1906) ,のち教授。6年後にパリ大学で教鞭をとり,その後コレージュ・ド・フランスの教授となった。最も重要な業績は現在ルベーグ積分と呼ばれている積分に関する研究 (1902) である。彼は E.ボレル,C.ジョルダンなどにより発展せられた測度論の影響を受けて,1901年に彼自身の測度論を立て,翌年それを基礎にして定積分の新しい定義を確立した。ルベーグ積分によってフーリエ解析はその後著しく発展した。サントゥール賞 (17) ,パリの科学アカデミー会員 (22) ,その他外国の科学団体の名誉会員に選ばれた。主著『積分と原始関数の研究』 (04) ,『三角級数』 (06) 。
ルベーグ
Lebègue, Nicolas Antoine
[生]1631. ラン
[没]1702.7.6. パリ
フランスのオルガン奏者,作曲家。 J.シャンボニエールまたは E.リシャールに学び,1664年パリのサン・メリ聖堂のオルガン奏者に就任,78年以降は宮廷オルガン奏者を兼務した。3巻のオルガン曲集 (1676,79,85) と2巻のクラブサン曲集 (77,87) を出版。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
ルベーグ
フランスの数学者。1920年パリ大学,1921年コレージュ・ド・フランス各教授。学位論文《積分,長さ,面積》(1902年)によりルベーグ積分を創始,実変数関数論,フーリエ級数論,ポテンシャル論等に一転機を画した。位相幾何学,解析学全般にも重要な業績が多い。
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内のルベーグの言及
【実関数論】より
…微積分学も集合論の基礎のうえに立って近代化され,現代の実関数論にまで深められたのである。 実関数論において中心的役割を果たすのは,20世紀の初めにH.ルベーグの画期的な学位論文(1902)によって創始された測度と積分の理論である。彼は直線上の図形の長さ,平面図形の面積,空間図形の体積の概念を,できるだけ一般な図形の範囲に拡張することを考え,測度という概念を導入し,それをもとにして積分の理論を展開した。…
【測度】より
…直線上の図形の長さ,空間図形の体積の概念についても同様なことがいえる。 20世紀の初めにH.ルベーグは,測度と名付ける次のような概念を導入して,その具体的構成法を与えた。すなわち,集合Aの測度μ(A)とは,長さ,面積,体積の概念の拡張であって,可算無限個の集合A1,A2,……,An,……が測度をもちどの二つも交わらないならば,それらの合併集合A=A1∪A2∪……∪An∪……も測度をもち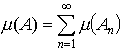 となるものである。…
となるものである。…
※「ルベーグ」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 


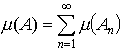 となるものである。…
となるものである。…