精選版 日本国語大辞典 「情報理論」の意味・読み・例文・類語
じょうほう‐りろんジャウホウ‥【情報理論】
改訂新版 世界大百科事典 「情報理論」の意味・わかりやすい解説
情報理論 (じょうほうりろん)
information theory
情報とは,日常用語としては“ある事柄についての知らせ”をいうが,情報理論で取り扱う情報は,通信システムや制御システム中を流れる科学や工学の対象としての情報をいう。情報というものを自然科学ならびに工学の対象として研究すべきことを最初に提唱したのはN.ウィーナーであった。ウィーナーは第2次世界大戦中に高射砲の制御の問題を取り扱っている間に,レーダーと高射砲から構成される制御システムの中に情報の流れが重要な働きをしているのに気づき,さらに人間の神経系と運動に関しても類似の対象としての情報の重要性を指摘した。
しかしながら,具体的に情報理論を数学を用いて体系化したのは,C.E.シャノンの功績である。1948年に,彼は《通信の数学的理論》という論文をベル電話研究所の機関誌に発表しており,その理論大系のもつすばらしさで一躍脚光を浴びることになった。
シャノン自身は電気通信工学を専門とし,電気通信を抽象化して,情報理論を体系化したのであるが,そのもでるは人間と人間,あるいは人間と機械,機械と機械などのあらゆるコミュニケーション過程に適用可能である。このようにして電気通信工学だけでなっく言語学,社会学,生物学,医学,経済学などあらゆる学問領域に大きな影響を与えている。
図はシャノンの通信系のモデルを示したものである。ここで情報源は伝送すべき情報を発生する源であり,具体的には情報は,情報源の発生する記号(シンボル)によって運ばれる。記号は文字(レター)ともいわれ,この集合がアルファベットである。一連の記号列を通報(メッセージ)という。符号器は,情報源からの出力記号列を,通信路を通して伝送しやすい形に変換する。これを符号化と呼ぶ。符号化の目的には,いろいろなものが考えられる。情報源の出力系列の中から冗長の部分を取り除く符号化は情報源符号化という。通信路に誤りが生じたとき,この影響を受けにくいように変換する符号化は通信路符号化という。通信路で信号が他人に傍受されても,これが容易に解読されないように変換する符号化は暗号化と呼ばれる。通信路は物理的に符号器の出力を復号器まで伝達する媒体で,音波,光,電気信号などがある。具体的には空気,光ファイバー,より銅線,同軸ケーブル,電波などがある。一般には雑音の混入が考えられる。復号器は通信路からの受信信号を受信し,これから情報源の出力系列を復元することを目的とする。受信目的というのは最終的な情報の受容者である。
このモデルは電気通信系を介在しての通信のみならず,人間と人間との間の音声による通信,あるいは神経系による刺激の伝達などにも適用される。このモデルにより,シャノンは情報源から発生する情報量を確率論を用いて定量化した。すなわち,情報源から発生する記号のもっている情報源Iは,その記号の生起確率をpとすると,I=log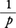 で表されること,またこの情報源の定義から出発して,通信路のモデル化を行うとともに通信路が運びうる情報量の限界,すなわち通信路容量を明らかにした。
で表されること,またこの情報源の定義から出発して,通信路のモデル化を行うとともに通信路が運びうる情報量の限界,すなわち通信路容量を明らかにした。
また情報源から発生する情報を二元符号化する場合に,二元符号の平均符号長には下限値があり,この下限値が情報源のエントロピーに等しいこと(シャノンの第1基本定理),また誤りのある通信路において,その通信路容量以下の伝送速度では誤りのない符号化が存在すること(シャノンの第2基本定理)などの重要な定理を証明した。シャノンの業績を記念して情報量の単位としては〈シャノン〉が採用されている(実際にはまだピットが用いられることも多い)。情報理論は狭い意味では,上記のシャノンの理論を中心とした分野を指すが,広い意味では,情報に関する諸理論,すなわち信号理論,パターン認識理論,言語理論,人工知能論などをも含む。シャノンの確立した情報理論は,主として情報を運んでいる記号の確率的性質に着目する。その後,言語については,とくに構造に注目してN.チョムスキーらにより言語理論の体系化がなされ,さらに自然言語処理を目的として意味論も展開されている。人口知能研究との関連においては学習機構推論機構,知識構造などの体系化も重要な問題となっている。ロボット工学との関連では,パターン認識,とくに情景解析の分野が研究の対象にされるなど,広い意味での情報理論は,情報科学ならびに情報工学のあらゆる基礎分野を包含し,今後の展開が期待されている。
執筆者:宮川 洋
音楽
情報理論が提出した要素の確率状態による数量化は,音楽の内在的な要素の分析を行ってきた音楽研究でも早くから受け入れられた。この点で評価されるべきは,アメリカの数学者G.D.バーコフが1930年代に行った一連の〈美的尺度acsthetic measure〉の研究である。彼は,情報理論の定式化以前に明確な手順によって音楽の客観的特徴を計算し,統一と複雑さの比によってこの尺度の値を求め,さらに,同じ値になるような創作も試みている。情報理論が提出されたころは,シャノン夫婦を含め,音楽のシミュレーションや,作曲家の間の個人様式の比較などが試みられた。60年代までは,マルコフ過程の次数を上げてデータをとれば,分析,合成とも精度が上がると思われていたが,音楽では拍子構造における強拍と弱拍の区分のように,分析対象の音が等価でないことが多いため,結局,この理論による分析はあまり成功していない。しかし音楽認知のモデルとしての応用や,分析した結果を合成することができるような定量的分析を可能にしたこと,さらに,音楽の意味論にかかわらず分析が行われたことなど,この理論による研究や標榜(ひょうぼう)していない領域にも大きな意義を与えている。
執筆者:徳丸 吉彦
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
図書館情報学用語辞典 第5版 「情報理論」の解説
情報理論
出典 図書館情報学用語辞典 第4版図書館情報学用語辞典 第5版について 情報
百科事典マイペディア 「情報理論」の意味・わかりやすい解説
情報理論【じょうほうりろん】
→関連項目時系列
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「情報理論」の意味・わかりやすい解説
情報理論
じょうほうりろん
information theory
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
日本大百科全書(ニッポニカ) 「情報理論」の意味・わかりやすい解説
情報理論
じょうほうりろん
information theory
通信における情報伝達の数学的理論のこと。20世紀なかば以降、情報科学の基盤を形づくっている。
[編集部]
世界大百科事典(旧版)内の情報理論の言及
【情報科学】より
…一方,C.E.シャノンは通信の本質を探究する中で,情報の伝達すなわち通信の現象にひそむ情報の本質構造を数学理論として認識し体系化することに成功した。これが1948年に発表された情報理論である。これは情報量を,状況の不確定度であるエントロピー概念を用いて確率論を援用し定義するもので,情報科学に高度の理論的基礎を与えた。…
【情報量】より
…これが可能であれば,それは記憶装置の有効活用であり,データ通信においては通信接続時間の短縮により通信コストの削減という経済的な効果を生む。
[情報源]
データ系列の中にどれほどの冗長性が含まれ,それを除去すると残る本質的な情報は定量的に測っていくらなのかということを論じるために,情報理論では,数学的にきちんと定義された〈情報源〉という,データ系列を生成するモデルが導入される。たとえば,1から6までの整数が等確率1/6で出現する情報源は公平なサイコロ振りの数学モデルである。…
※「情報理論」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...