集合論（読み）シュウゴウロン

デジタル大辞泉

しゅうごう‐ろん〔シフガフ‐〕【集合論】

数学の一部門で、集合の性質を研究する学問。19世紀末、ドイツのゲオルク＝カントルが創始。

出典　小学館

精選版 日本国語大辞典

しゅうごう‐ろん シフガフ‥【集合論】

〘名〙 集合の性質を研究する数学の一分科。一九世紀末、ドイツの数学者ゲオルク=カントルによって創始された。〔頭脳（1958）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

集合論
しゅうごうろん

1874～1897年にカントルによってつくられた数学の一分野。彼は集合を次のように定義した。「集合とは、明確に定義され、かつ互いに明確に弁別できるわれわれの直観あるいは思惟(しい)の対象mを、一つの全体にまとめたものMのことである。mをMの元(げん)という」。集合は、与えられた性質を満たす対象の全体としても定義できる。集合概念は広い概念で、無制限に用いるとパラドックスを引き起こす。公理的な方法、あるいは非常に大きい集合を、集合とは異なる「類」という概念で区別することによって、パラドックスは避けられることがわかった。

［西村敏男］

基本概念

集合論のもっとも基本的な概念は、対象mが集合Mの元である（m∈Mと書く）ということである。元を含まない集合を空(くう)集合といい∅で表す。｛a, b,……, m,……｝によってa, b,……, m,……を元とする集合を表す。同じ元からなる二つの集合aとbは同じ集合と考えa＝bによって表す。aの元がすべてbの元であるときaはbの部分集合であるといいa⊂bで表す。数学の諸概念は集合と集合間の関係a∈bから論理的に構成できる。たとえば自然数0, 1, 2,……はそれぞれ集合∅,｛∅｝,｛∅,｛∅｝｝,……と定義される。一般に順序数αはαより小さい順序数全体の集合と定義し、その大小関係α＜βをα∈βのこととする。順序対(a, b)を集合｛｛a｝｛ab｝｝のこととすれば、(ab)＝(cd)のときa＝cかつb＝dとなる。集合AとBに対し集合ABを、Aの元aとBの元bの順序対(ab)全体からなる集合とし、AとBの直積(ちょくせき)という。A、Bをそれぞれx軸上、y軸上の実数の全体とすれば、ABは平面上の点の座標の全体となる。Nを自然数全体の集合とする。m, n∈Nなるmとnの間に大小関係m＜nすなわちm∈nが成り立つとする。Eをx∈yでx, y∈Nであるような順序対(x, y)の全体からなる集合とすれば、m＜nとは(m, n)∈Eのことであり、E⊂NNである。

　このように、集合Aの元の間の関係とは、R⊂AAという集合Rのことと考えれば、「関係」も集合概念になる。集合Aの元の間の関係a＜bについて、a＜bかa＝bのときa≦bと書くことにする。Aの任意の二元xとyについてx≦yかy≦xが成り立ち、x≦yかつy≦xのときx＝yで、x≦yかつy≦zのときx≦zが成り立つとき、関係（＜）をAの順序という。集合Aの各元の間にこのような順序があるときAを順序集合という。集合Aの元を集合Bの元に対応させる関数F(a)＝bは(a, b)∈Fと考えれば、F⊂ABとなるような集合Fのことで、「関数」も集合概念になる。関数の場合には、F(a)＝bかつF(a)＝cならばb＝cという一意性を要求する場合が多い。一意性のほかにF(a)＝cかつF(b)＝cならばa＝bという条件を満たせば、Fは一対一の対応といわれる。集合AとBの間に一対一対応があるというのは、Aの各元にBのちょうど一つの元が、Bの各元にAのちょうど一つの元が対応するような関数FがあるということであるAとBの間に一対一対応があれば、AとBとは同じ濃度をもつといい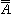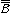＝と書く。AとBの間の一対一対応はないが、Bの部分集合とAの間に一対一対応があれば、Bの濃度はAの濃度より大きいといい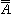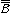＜と書く。Aの濃度とはAの元の個数に相当する概念で、個数の概念を一般の無限集合にまで拡張したものである。

　nを自然数とすればnはnより小さい自然数全体からなる集合である。nと一対一対応のある集合を濃度nの有限集合、そうでない集合を無限集合という。Nと一対一対応のある集合を可算無限集合という。その濃度をℵ₀と書く（ℵはヘブライ文字アレフで、ℵ₀はアレフゼロと読む）。Aを任意の集合とし、Aの部分集合の全体からなる集合をAのべき集合といいP(A)と書く。このときP(A)の濃度はAの濃度より大きい。これをカントルの定理という。Nを自然数全体からなる集合とすれば、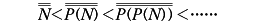

であり、無限集合の濃度にも無限の段階がある。実数の全体からなる集合の濃度はP(N)の濃度と等しく、これをℵと書き、連続体の濃度という。Aが順序集合であって、Aのどの部分集合にも最小元があるとき、Aは整列集合であるという。順序数の任意の集合は、順序数の大小関係で整列集合である。自然数に関する数学的帰納法の拡張として、「αを任意の順序数とする。β＜αなるすべてのβに対して命題P(β)が成り立つと仮定してP(α)が証明できるとする。このときすべての順序数xに対してP(x)が成り立つ」ことが証明できる。これを超限帰納法という。整列集合Aの各元は順序数によってa₀, a₁, a₂,……, a_ω, a_ω+1,……のように並べることができる。後述する選択公理を用いると、「任意の集合Aは、適当な順序をAの元の間に与えることによって整列集合にすることができる」ことが証明できる。これを整列可能定理という。またこの公理を用いると、濃度もその大小の順序で整列集合であることがわかる。ℵ₀が最小の無限濃度で、αを順序数としてα番目の無限濃度をℵ_αと書く。ℵ₀＜ℵ₁＜ℵ₂＜……＜ℵ_α＜……となる。このとき「ℵがどのℵ_αになるか」という問題を連続体問題といい、集合論の基本的な重要問題であった。ゲーデルはℵ≠ℵ₁と仮定してもツェルメロ‐フレンケルの公理的集合論と矛盾しないことを証明（1938）、コーエンはℵ≠ℵ₁と仮定しても矛盾しないことを証明した（1963）。

［西村敏男］

公理的集合論

集合論の公理系を最初に与えたのはツェルメロである（1908）。その後この公理系は拡張され整備されて、今日ツェルメロ‐フレンケルの公理的集合論とよばれるものになった。ここでは「xは集合である」と「y∈x」という二つの概念は未定義概念として扱われる。次にその公理を与える。

(1)空集合が存在する。

(2)同じ元をもつ集合xとyは同じ集合である。これを外延性の公理という。

(3)集合xとyに対して｛x, y｝は集合である。

(4)集合xに対し集合yが存在して、u∈yとはu∈z∈xとなるような集合zが存在することである。これは集合族xの元である集合の和集合yを与えるものである。

(5)集合xに対しそのべき集合が存在する。

(6)集合xと命題A(u)に対して集合yが存在して、u∈yとはu∈xかつA(u)なることである。これを分出公理という。

(7)A(u, v)を命題とし、任意のu、v、wについてA(u, v)かつA(u, w)ならばv＝wとする。このとき任意の集合xに対し集合yが存在して、z∈yとはu∈xかつA(u, z)であるuが存在することである。これは集合xの一意写像yが集合として存在することを主張するもので、フレンケルによって導入された（1922）。これを置換公理という。

(8)空でない集合xが存在して、v∈xならばw∈xなるwでv⊂wかつv≠wとなるwが存在する。このxは無限個の元を含むことになる。これを無限公理という。

(9)A(u)を命題とする。A(x)となるxが存在すれば、A(x)を満たすxで、y∈xなるどのyもA(y)を満たさないようなxが存在する。この公理は次の選択公理のもとでは、……∈x₃∈x₂∈x₁のような無限下降列が存在しないことと同等であり、正則性の公理という。

(10)xを集合族としその各元は空集合でなく、xのどの二元も共通部分をもたないとする。このとき、xの各元のちょうど一つずつの元を含むような集合yが存在する。この集合yをxの選択集合といい、この公理を選択公理という。これはツェルメロによって公理として導入された（1904）。数学の多くの定理の証明に用いられるが、この公理の使用には論議が多い。

　公理(6)と(9)の命題A(u)と(7)の命題A(u, v)は無限個あるので、これらの公理はそれぞれ無限個の公理からできている。

［西村敏男］

『松村英之著『集合論入門』（1974・朝倉書店）』▽『難波完爾著『集合論』（1977・サイエンス社）』▽『西村敏男・難波完爾著『公理論的集合論』（1985・共立出版）』

[参照項目] | 関数 | 濃度

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

集合論 (しゅうごうろん)
set theory

集合として扱われるものを使った推論。集合という概念を定義することを提案し，有効な理論を打ち立てたのはG.カントルである。カントルは次のように集合を定義した。〈集合とは，われわれの直観あるいは思考の対象であって，確定し，かつ明確に区別されるものを一つのまとまりとして集めたものである〉。すなわち，われわれの直観または抽象的思考によって考えうるものを元（または要素）と呼び，そのような元のうち，いくつかの条件を満たすものを集めるというようにして集めたものが集合であって，ある元がその集合に入っているかどうかとか，二つの元が相等しいかどうかということが明確になっていることが要請されているものである。

　カントルが構成した集合論の主要な部分は，集合の元の多さを示す濃度の概念，さらには順序数の概念の導入とそれらの理論の構成であるといえる。しかしながら，集合の定義があいまいさを内蔵しており，そのためにいくつかの逆理が生まれた。1897年にブラリ・フォルティCesare Burali-Forti（1861-1931）は，〈すべての順序数の集合〉を考えて矛盾を導き出した。カントル自身も99年に〈すべての集合の集合〉Mを考えると，Mの部分集合の全体はMと一致し，カントル自身が1890年に証明した次の定理に反するので矛盾を含むことに気づいた。定理〈どんな集合Mについても，Mの部分集合全体の集合はMより大きい濃度をもつ〉。また，〈すべての集合の集合〉MはM自身も含むという変なことになるので，B.A.ラッセルは1905年に，〈自身を元としては含まない集合全部の集合〉Nを考え，次のような矛盾を指摘した。N∈NならNの定義によって，N∉N。またN∉Nなら，Nの定義によってN∈N。このようなことから，集合論の論理的基礎を再検討する必要が感じられ，その一つの方法として公理による構成が考えだされた。現在，集合論の公理系として利用されているものには二つの体系があり，一つはツェルメロ=フレンケルの集合論Zermelo-Fraenkel set theory，他はベルナイス=ゲーデルの集合論Bernays-Gödel set theoryと呼ばれている。いずれにしても集合の構成を規制することによって，心配のない理論にしようというのである。これらの公理系によれば，（1）自然数全体は集合をなし，（2）一つの集合の部分集合全体も集合をなし，（3）二つの集合の直積A×Bも集合をなし，（4）集合Aから集合Bの中への写像fがあれば，fの像全体f（A）も集合であり，さらに，（5）一つの集合Aにおけるある条件（これも公理によって規制される）を満たす元の全体も集合であるので，よほど奇妙な集りを考えないかぎり集合であると思ってよいだろう。カントルが集合と定義した内容のものは必ずしも集合ではないので，それを領域と呼ぶことがある。

　また，公理のうちで，特別視されているものに選択公理がある。それは，〈ある集合Mの部分集合の集りNがあり，Nの各元は空集合でないとき，Nの各元sに対して，sの元を一つずつ対応させることができる〉というものであり，何となく当然のように聞こえるが，これを公理として取り上げる理由は，Nが非常に大きい濃度をもっているかも知れないので，〈ものすごい無限回の操作をいっぺんにすます〉という特殊なことを含んでいる。それに対し，他の公理は〈有限の手続による〉と考えられる操作しか含んでいない。無限回操作を含むから，選択公理を認めるのは危険であるという考えもあるが，〈他の公理全体の系が矛盾を含まないなら，選択公理を加えた系も矛盾は含まない〉ことが証明されているから，選択公理は認めてもよいと考えられている。

連続体問題

可算無限の濃度と連続体の濃度（実数全体の集合の濃度）との間に他の濃度は存在するか，というのが連続体問題である。もっと一般に，μが無限の濃度のとき，2^μとμとの間に他の濃度があるかというのが一般連続体問題である。そして，それぞれについて，〈存在しない〉とする命題が，連続体仮説，一般連続体仮説である。連続体仮説（または一般連続体仮説）を公理として採用したとき，通常の公理系とは独立であることが証明されている，ということは，集合の構成を制限することによって一般連続体仮説の成り立つような集合の体系を作ることもでき，また，反対に，実数全体の集合の部分集合を適当にとれば，濃度が可算無限より大きく，実数の濃度より小さいものがとれる（が，それはふつうの構成法ではできない）ことを示している。

点集合論

ある次元のユークリッド空間Eの部分集合は，Eの点を元としているので点集合と呼ばれる。点集合についての理論を点集合論と呼び，これが集合論の主要部分と考えられた時代もあるが，その内容の大部分は，現在では〈位相空間の部分集合〉として一般化された立場で扱われるようになった。
→集合
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

集合論【しゅうごうろん】

集合の性質を研究する数学の一部門。19世紀末にG.カントルが創始，古典的集合論の本質的部分を完成したが，彼の集合の定義から論理的に幾つかのパラドックスが生ずることが明らかになり，数学基礎論を生む契機となった。またパラドックスを避けるため公理的集合論が建設された。現代数学はすべて集合論に基礎をおいて発展しているといえる。
→関連項目数学｜デデキント｜濃度（数学）｜フォン・ノイマン

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

集合論
しゅうごうろん
set theory

集合を取扱う数学の一分科である。 G.カントルが，1874～98年，ほとんど独自に確立した理論である。カントルは，数学的無限を明確に定義して，無限に関する算数ともいうべき理論を築き上げた。これは算数の対象である有限の数をも含めた無限の数に対する新しい算数であって，その基本になる概念には，集合，対応，あるいは写像，順序などがある。集合論は 20世紀に入ってめざましい発展を続け，特に数学および論理学の両分野において，重要な意義をもっている。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の集合論の言及

【数学基礎論】より

…数学は矛盾のない理論体系と信じられており，諸科学の中でももっとも厳密な論証を誇るものとして，およそそのよって立つ基盤がゆらぐようなことがあろうなどとは考えられなかった。ところが，19世紀末G.カントルによって創設された集合論はまもなく逆理を生じた(パラドックス)。カントル自身が発見した逆理(1899)，ブラリ=フォルティの逆理(1897)やラッセルの逆理(1903)がそれである。…

【無限】より

…ただし無限小，すなわち微分の解釈については議論が分かれ，可能的あるいは現実的とされて決着がつかなかった。　現実的無限の数学の完成は，19世紀後半の集合論にいたってである。集合論は解析学の合理的再建を果たすとともに，無限数の理論たる超限数論への道を開いた。…

【論理学】より

…さらに，個体としての〈もの〉の一定の枠を想定し，その枠内で〈もの〉の組がつくる集合――これを述語という――を考え，これら個体と述語の結合を記述する命題の相互関係を考察する論理学は，(一階の)述語論理学と呼ばれる。また，考えうる最も一般的な集合の規定を主題とする論理学は，集合論と呼ばれる。そして命題論理学，述語論理学，集合論は，たがいに後のものが前のものを包括するという形で展開されるのである。…

※「集合論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」