ボルテラ
ぼるてら
Vito Volterra
(1860―1940)
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ボルテラ
Volterra
イタリア中部,トスカナ地方のエトルリア起源の古代都市。エトルリア語でウェラトリVerathri,ラテン語でウォラテラエVolaterrae。チェチーナ川とエラ川を見下ろす急峻な丘の上に前7世紀軍事都市として建設され,銅の生産と内陸通商によって前4世紀から前1世紀にかけて最も栄えた。エトルリア12都市同盟の一つ。考古学資料は新石器時代から出土するが,一定規模の集落を形成したのはビラノーバ文化時代になってからである。前7世紀エトルリア人の都市が建設されると急速に人口も増え,城壁も数次にわたり拡張された。城壁に施された二つの城門,ディアナ門とアルコの門のうち,前者はエトルリア建築におけるアーチ門として重要である。周囲には多くの墓があり,とくに前3世紀以降の石棺型テラコッタ製骨容器の浮彫の人物像は強調された写実主義を示す例として有名である。
執筆者:青柳 正規
ボルテラ
Vito Volterra
生没年:1860-1940
イタリアの数学者。積分方程式,積分微分方程式,汎関数論などを研究。純粋数学の研究のみならず,物理学や生物学と関連した応用数学的研究も数多く行う。とくに晩年の15年間に行った数理生態学の研究は著名である。これは娘婿の水産学者ダンコナU.D'Ancona(1896-1964)から聞いたアドリア海における魚種交代現象の話に端を発するもので,彼はこの現象を説明すべく,1926年に被食者と捕食者の個体数変動に関する微分方程式モデルを,アメリカのA.J.ロトカと独立に,提出した。そして以後,種間競争のモデルをも含めて,さらに詳しく深い研究を続け,ロトカなどと並んで数理生態学の開拓者となった。これらの研究は彼がファシストへの忠誠を拒否し,イタリアのアカデミズムからも追われた困難な状況の中で行われた。
執筆者:太田 邦昌
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ボルテラ
Volterra, Vito
[生]1860.5.3. アンコナ
[没]1940.10.11. ローマ
イタリアの数学者。ピサ大学に学び (1878~82) ,E.ベッチの強い影響を受ける。ピサ大学の力学教授 (83) 。この頃から汎関数の一般理論の研究を始める。汎関数の概念から解析学の新しい領域が生れた。彼はその解析的方法を光学,電磁気学,弾性理論に応用してよい結果を得た。トリノ大学の力学教授 (90) 。ローマ大学の数理物理学教授 (92) 。 1905年,イタリア王国の上院議員に選ばれた。第1次世界大戦中は,すでに 55歳であったにもかかわらず,イタリア空軍に参加し,飛行船技術の向上に努力。彼は飛行船にそれまで使っていた水素をヘリウムに切替えた。戦後,数理生物学を研究,生態系の数学的モデルを考え,物理学にも応用した。ムッソリーニのファシスト政府への忠誠を拒絶して,31年にローマ大学から,続いてあらゆる公職から追われ,寂しい晩年を過した。主著『汎関数の理論および積分方程式,積分微分方程式の理論』 (1930) 。
ボルテラ
Volterra, Daniele da
[生]1509. ボルテラ
[没]1566.4.4. ローマ
イタリアの画家。本名 Daniele Ricciarelli。シエナのソドマに師事,のちミケランジェロの影響を受け,彼の様式を受継いだ。 1559年教皇パウルス4世の命を受けてミケランジェロの『最後の審判』の裸体の人物に衣を描いた。おもな作品『キリストの降架』 (1541,ローマ,トリニタ・デイ・モンティ聖堂) ,『幼児虐殺』 (47,ウフィツィ美術館) 。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のボルテラの言及
【ガウゼの法則】より
…このような考えはC.ダーウィンの自然淘汰説の主要な柱でもあったため,多くの研究者によって古くよりいろいろな形で主張されてきた。数式モデルによってこのような考えに理論的な考察を加えたのはボルテラV.Volterra(1926)とロトカA.J.Lotka(1932)が最初であるが,1934年にソビエトのガウゼG.F.Gauseが酵母菌とゾウリムシを用いて初めて詳細な実験的研究を行い,種間競争によって一方が他方を駆逐してしまうという現象を明確に実証したところから,後にこのような考えがガウゼの法則(仮説)と呼ばれるようになった。この呼び方には異論もあり,競争的排除則あるいは競争的置換則と呼ばれることもある。…
【積分方程式】より
…これが積分方程式の始まりである。しかし積分方程式を系統的に論じたのは,ボルテラV.Volterra(1860‐1940)とフレドホルムE.I.Fredholm(1866‐1927)である。 一般的な形として,f(x),K(x,y)を既知関数,φ(x)を未知関数とするとき,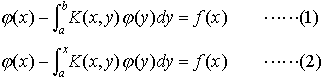 はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…
はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…
【ガウゼの法則】より
…このような考えはC.ダーウィンの自然淘汰説の主要な柱でもあったため,多くの研究者によって古くよりいろいろな形で主張されてきた。数式モデルによってこのような考えに理論的な考察を加えたのはボルテラV.Volterra(1926)とロトカA.J.Lotka(1932)が最初であるが,1934年にソビエトのガウゼG.F.Gauseが酵母菌とゾウリムシを用いて初めて詳細な実験的研究を行い,種間競争によって一方が他方を駆逐してしまうという現象を明確に実証したところから,後にこのような考えがガウゼの法則(仮説)と呼ばれるようになった。この呼び方には異論もあり,競争的排除則あるいは競争的置換則と呼ばれることもある。…
【生態学】より
…そこでは,害虫の抑圧または有用魚の増殖という課題からして,初めから個々の種の個体数が対象であった。その発展のきっかけはA.J.ロトカ(1925)とV.ボルテラ(1926)の数理モデルの提出とG.F.ガウゼ(1934)の実験的研究で,そのころからこれは個体群生態学と呼ばれるようになった。動物の個体数は生まれれば増え死ねば減る。…
【積分方程式】より
…これが積分方程式の始まりである。しかし積分方程式を系統的に論じたのは,ボルテラV.Volterra(1860‐1940)とフレドホルムE.I.Fredholm(1866‐1927)である。 一般的な形として,f(x),K(x,y)を既知関数,φ(x)を未知関数とするとき,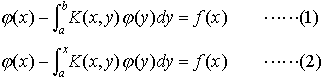 はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…
はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…
※「ボルテラ」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
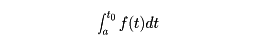
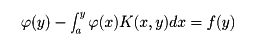
 =(I+TK+TK2+……)fで与えられる。このオペレーターI,TK,TK2……は、
=(I+TK+TK2+……)fで与えられる。このオペレーターI,TK,TK2……は、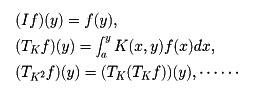


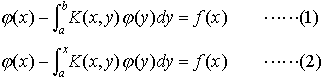 はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…
はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…