改訂新版 世界大百科事典 「フェルミ準位」の意味・わかりやすい解説
フェルミ準位 (フェルミじゅんい)
Fermi level
フェルミ=ディラック分布によれば,絶対温度Tの熱平衡状態において,粒子がエネルギーεの状態を占める確率は,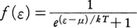
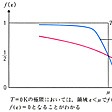
で与えられる(kはボルツマン定数)。この表式の中に現れるエネルギーμをフェルミ準位という。フェルミ分布関数f(ε)の値はフェルミ準位μにおいて(ε=μ)ちょうど1/2になり(図1),このエネルギーを境にして,熱エネルギーkTの数倍程度の幅でほぼ満席の状態(f(ε)~1)からほぼからっぽの状態(f(ε)~0)への遷移が起こる。多くの現象において,フェルミ準位近傍のエネルギーをもつ電子だけがそれに関与するが,これはμよりある程度以上低いところにいる電子はまわりがすべて満員で身動きできないし,逆に高いところにはもともと電子がほとんどいないためである。
数学的には,フェルミ準位は,分布関数から計算される電子数を与えられた電子数と等しくさせるためのパラメーターとして導入される。フェルミ分布の表式からわかるように,μが高(低)くなれば分布関数は全体として図1において右(左)へ平行移動することになり,その結果,全電子数は増加(減少)する。半導体の場合,フェルミ準位のこのような役柄がとくに顕著に現れ,有用な概念となる。まず固有(真性)半導体では,フェルミ準位は充満帯と伝導帯の間のギャップのほぼ真ん中にある(図2-a)。伝導帯までのびているわずかな分布の裾野と充満帯に生じている少数の空席が伝導電子と正孔に対応する(伝導電子と正孔とは同数生ずる)。ドナーを加えてn型半導体にすると全電子数が増加するので,μは高くなり,ほぼドナー準位まで上がる(図2-b)。逆にアクセプターを加えてp型半導体にすると電子数が減り,μはアクセプター準位の近くまで下がる(図2-c)。半導体の場合,ギャップの部分には電子を収容する状態がほとんど存在しないため,比較的少数の電子の増減によってフェルミ準位が大きく上下に動く。
二つの体系が熱平衡状態にあるとき,両者のフェルミ準位は一致する。フェルミ準位の異なる体系を接触させると,それが同じになるまで高いほうから低いほうへ電子が移る。ただしこの場合のフェルミ準位の動きは,前述の原因によるのではなく,むしろ次の静電的効果から起こる。すなわち,フェルミ準位の高いほうから低いほうへ電子の移動が起こる結果,両体系は互いに反対符号に帯電し,その間に電位差(接触電位差と呼ぶ)を生じ,この電位差が加わるため両者のフェルミ準位が等しくなるのである。例えば,n型半導体とp型半導体を接触させると,前者から後者へ電子が移り,図3のような状態で熱平衡に達する。この二つの半導体を,単なる接触でなく,つなげたものをp-n接合と呼び,pからnへの方向には電流を通すが,逆方向には通しにくいという整流作用をもつので重要である。
執筆者:黒沢 達美
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「フェルミ準位」の意味・わかりやすい解説
フェルミ準位
ふぇるみじゅんい
Fermi level
電子、陽子、中性子など、フェルミ‐ディラック統計に従う粒子系の分布は、低温では、あるエネルギー準位より低い状態はほとんど完全に粒子で占められ、高い状態にはほとんど粒子が存在しない。この境目のエネルギー準位をフェルミ準位またはフェルミ・エネルギーとよぶ。のように、粒子がエネルギーεの状態を占める確率はフェルミ分布関数
f(ε)=1/[e(ε-μ)/kT+1]
で与えられる。この式で、μがフェルミ準位である(kはボルツマン定数、Tは絶対温度)。
金属内の伝導電子は、周りにいる電子や原子芯(しん)(伝導電子を放出した残りのイオン)から、時間的・空間的に変化する複雑な力を受けながら動き回るが、これを正確には扱えないので近似を行う。もっとも簡単なものは、これらの力を時間的にも空間的にも平均すればゼロになると考える自由電子模型である。その場合、絶対零度(T=0)のときのフェルミ準位はμ=(h2/8m)(3n/π)2/3で与えられる。hはプランク定数、mは電子の質量、nは単位体積中の伝導電子数である。μは温度が室温程度に上がってもあまり変化しない。絶対零度でも電子は飛び回っているわけであるが、そのうちで最大エネルギーのものはμ=pF2/2mから決まる大きさpFの運動量をもっていることになる。このpFをフェルミ運動量という。電子が自由でないと、とりうるエネルギー値の分布はバンド構造になるが、フェルミ準位が許される値のなか(バンド内)にできるか、それを外れたギャップのところにできるかによって、金属になったり半導体や絶縁体になったりする。
また、kをボルツマン定数として、μ=kTFと置いたときのTFのことをフェルミ温度といい、通常の金属で数万度の程度になる。
[小出昭一郎・小形正男]
化学辞典 第2版 「フェルミ準位」の解説
フェルミ準位
フェルミジュンイ
Fermi level
粒子間相互作用を無視した1体近似でフェルミ統計に従う粒子の多体系を扱う場合,エネルギーεの状態を絶対温度Tにおいて占める粒子数の相対値は,フェルミ-ディラック分布関数,
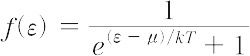
で与えられる.ここで,μはf(ε)をすべてのεについて加えた和が粒子の総数に相当するという条件で決まるパラメーターで,化学ポテンシャルに等しい.フェルミ統計ではこのμをフェルミ準位とよぶ.絶対零度ではフェルミ準位より低いエネルギーの状態はパウリの原理で許される最大限まで粒子が詰まり,フェルミ準位より高いエネルギーの状態は完全に空席になる.固体の電子論においては,フェルミ準位がエネルギー帯中にあるか,帯間のギャップ中にあるかによって金属と絶縁体の区別が生じる.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
ブリタニカ国際大百科事典 小項目事典 「フェルミ準位」の意味・わかりやすい解説
フェルミ準位
フェルミじゅんい
Fermi level
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
最新 地学事典 「フェルミ準位」の解説
フェルミじゅんい
フェルミ準位
Fermi level
多くの電子が存在する物質(多電子)系では,温度が絶対零度に近づくと,パウリの排他則に従って,系のエネルギーは最低状態からある程度上位のエネルギー準位までのエネルギー状態をとる必要がある。絶対零度の状態で,電子が下位のエネルギー準位から隙間なく占有されたときに取ることができる最大のエネルギー準位をフェルミ準位と呼ぶ。
執筆者:栗林 貴弘
出典 平凡社「最新 地学事典」最新 地学事典について 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...