ポテンシャル（その他表記）potential

デジタル大辞泉

ポテンシャル（potential）

１ 潜在的な力。可能性としての力。「事故のポテンシャルを予測する」
２ ある粒子がもつ位置エネルギーを、位置の関数で表したスカラー量。重力場の場合は重力ポテンシャルとよばれる。
３ ⇒電位

出典　小学館

精選版 日本国語大辞典

ポテンシャル

1. 〘 名詞 〙 ( [英語] potential )
2. ① 可能性としての力。潜在する力。
   1. [初出の実例]「開発により核兵器のポテンシャルをきりなく高めていくことで」(出典：作家ノート 虚構と真実（1967）〈石原慎太郎〉祖国について)
3. ② 数学および力学で、力の場Ｆの成分をそれぞれ Fx Fy Fz とするとき、そのｘ、ｙ、ｚによる偏導関数がそれぞれ Fx Fy Fz に等しいような関数ｕをＦに対していう。
4. ③ 静電場において、単位電荷のもつ位置エネルギー。静電ポテンシャル。電位。同様に静磁ポテンシャル（磁位）のことをいうこともある。〔物理学術語和英仏独対訳字書（1888）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

ポテンシャル
potential

微分することによって力が導かれるような場所の関数をポテンシャルと呼び，力学，電磁気学などの物理学において場を表すのに用いられる重要な概念である。ポテンシャルをU（x，y，z）とするとき，ベクトル解析の記号で力Fは，

　F＝－∇U＝－grad U　　　……（1）　

と表されるが，これはFのx，y，z方向の成分をF_x，F_y，F_zとすると，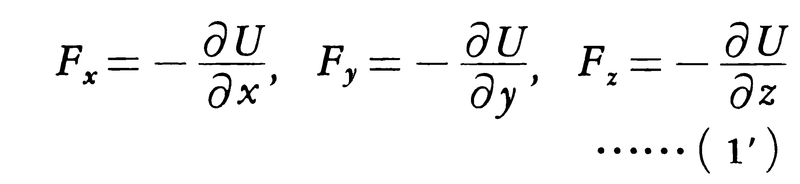

を意味している。このようにして与えられる力をとくに保存力というが，それは，この力を受けて運動する質点の力学的エネルギー（運動エネルギーと位置エネルギーの和）が保存されるからである。この際の位置エネルギー（ポテンシャルエネルギー）がポテンシャルUにほかならない。磁気的な力については後述するが，ベクトルポテンシャルと呼ばれるものも登場する。

　まず空間が一次元の場合，（1）は，

　F_x＝－\(\frac{dU（x）}{dx}\)

となる。したがって力は，関数Uのこう配の符号を変えたものとなる。角振動数ωで単振動をする単振動子（質量m）については，F_x＝－mω²xであるので，U＝1/2mω²x²となる（定義から明らかなように，Uには定数項だけの不定性がある。上の例ではU（0）＝0とした）。これを図に示したのが図1である。x＝x₁におけるこう配も，接線の形で示してある。図の例では，こう配は正なので力は負，つまり原点に向かっていることを表す。この力を受ける質点は，ちょうどポテンシャルの谷底に向かうような力を受けることがわかる。

　空間が三次元の場合の重要な例は，万有引力である。原点に質量Mの質点があるとき，距離rの位置にある質量mの質点は，中心に向かって大きさF＝GMm/r²の力を受ける（Gは万有引力定数）。これを導くポテンシャルは，

　U（x，y，z）＝U（r）＝－\(\frac{GMm}{r}\)　　　……（2）　

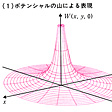
である。ここでr→∞でU→0となるように定数項をえらんだ。これを図に表したのが図2-aである。ただし，わかりやすい図にするためにz＝0として，xy面の上でUを表してある。あるいは，地図の等高線のように表したのが図2-bである。等高線は，実際の三次元空間では面となるので，等ポテンシャル面と呼ばれる。図2-bでは，そのz＝0の切口が同心円として現れているのである。

　上の例から推察できるように，力は，等ポテンシャル面に垂直で，ポテンシャルの低いほうへ向かう。もっと正確にいうと，最大傾斜の方向を向く。力の大きさは，その方向に測ったこう配である。質点は，やはり谷底にころげ落ちるような力を受けるといってよい。

　力が（1′）のように与えられる場合，積分可能条件，

　∂F_y/∂x－∂F_x/∂y＝0

　∂F_z/∂y－∂F_y/∂z＝0

　∂F_x/∂z－∂F_z/∂x＝0

が満たされ，場所AからBまで移動する間に力が質点にする仕事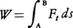は，2点A，Bを結ぶ道筋のとり方に依存しないことが証明される（積分は，ABを結ぶ曲線に沿って行われる線積分で，dsは曲線上の微小な長さ，F_tはFの曲線の接線方向の成分である）。さらにWは，点Aにおけるポテンシャルの値U_Aと，BにおけるそれU_Bとの差として表され，この結果，力学的エネルギーの保存則が導かれるのである。

　このようにポテンシャルは，エネルギーの保存則において中心的な役割を果たすばかりでなく，ベクトルである力を，Uというスカラー関数から導くという意味でも便利な量である。とくに万有引力のポテンシャル（2）は，次のポアソンの方程式，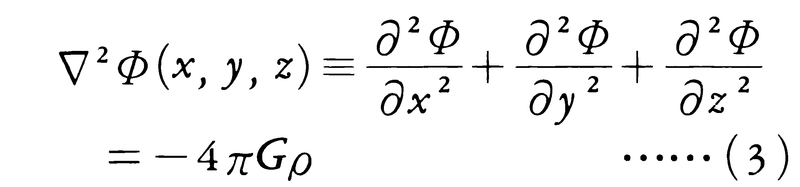

の解であるという事実も重要である。ここでρ（x，y，z）は質量分布を表し，またU＝mΦとおいた。静電気力（クーロン力）は，万有引力と同じく，距離の2乗に反比例するので，やはり（2）と同じく，距離に反比例するポテンシャルで表される。二つの電荷が異符号の場合は引力で，ポテンシャルも図2の型であるが，両電荷が同符号のときは斥力で，ポテンシャルは図3のようになる。電場Eを，

　E＝－∇φ＝－grad φ　　　……（4）　

の形で導くφ（x，y，z）をクーロンポテンシャルというが，正の電荷によって作られるものは正で図3の型，負の電荷によるものは負で図2の型となる。

　磁場，またはもっと正確には磁束密度Bは，

　div B＝0　　　……（5）　

を満足する。これは，磁力線には切れめがないことを表す。この性質をもつベクトルBは，任意のベクトルAを用いて，

　B＝rot A　　　……（6）　

と与えられる。すなわち（6）は自動的に（5）を満たすのである。このようにして導入されたAをベクトルポテンシャルと呼ぶ。このAに，スカラー関数Λ（x，y，z）を用いて，

　A→A＋∇Λ　　　……（7）　

という変換を施しても（6）は不変に保たれる。この変換（7）は，ゲージ変換と呼ばれ，量子力学との関連できわめて重要な意味をもつ。

　特殊相対性理論では，EとBとは別々のものではなく，ローレンツ変換によって互いに移り変わる。これに相当してクーロンポテンシャルφ（これをスカラーポテンシャルと呼ぶこともある）とベクトルポテンシャルとは，一つの四元ポテンシャルA_μに統合される（A₀＝－φ₀）。一般相対性理論では，重力のポテンシャルに相当するのは10個の計量テンソル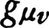である。万有引力のポテンシャルの満たす方程式（3）の拡張として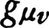，が満たすべき2階の偏微分方程式がアインシュタインの方程式である。以上，ポテンシャルについて具体的な例に沿って述べてきたが，この概念は一般のベクトル場においても同様に用いられる。
執筆者：藤井 保憲

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ポテンシャル
ぽてんしゃる
potential

力の場の各点に位置のエネルギーが定まる場合に、それをポテンシャルまたはポテンシャル・エネルギーとよぶ。「ポテンシャル」は潜在的の意。運動の勢いとして顕在する運動エネルギーに対していう。両者の和が一定で、エネルギーは顕在したり潜在したり互いに移り変わることができるのは、投げたボールやジェット・コースターなどの例にみられるとおりである。

［江沢　洋］

力の場とポテンシャル

質点の受ける力が空間の場所により定まっているとき、その空間を力の場という（たとえば、太陽の周りの重力の場、ただし、太陽は空間に静止しているものとする）。力の場に基準点Aをとり、そこに静止している質量mの質点を静かに（速度、加速度がゼロ、したがって無限の時間をかけて）別の点Pまで運ぶ仕事量W(A-Γ-P)が途中の道筋ΓによらずPの位置P(x,y,z)のみで定まる場合に限り
　　W(A-Γ-P)＝W(P)＝W(x,y,z)
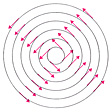
なる関数をこの力の場における質点mのポテンシャルとよび、この種の場を保存力の場という。Pまで運ぶ仕事が途中の道筋によって違うということがおこるのは、たとえば力の場が渦を巻いている場合である（図A）。

［江沢　洋］

ポテンシャルの場

保存力の場における質点mのポテンシャルは空間の各点で値（スカラー）が定まっているので、これも場である。座標の原点Oに固定された点電荷Qがあり、質点mも電荷qをもっているとし、二つの電荷は同符号とすれば、質点mにはOを中心とし逆二乗の法則に従う斥力が働く。この力は保存力であって、ポテンシャルの場W(x,y,z)をもつことが証明される。質点mに働く力は斥力で、点Oに近づくほど強くなるから、mをOの近くまで運ぼうとすれば、それだけ大きな仕事をしなければならない。それゆえz＝0の面上に限定してW(x,y,0)の値をグラフにすると図Bの(1)のような山の形（ポテンシャルの山）ができる。これがポテンシャルの場の一つの表し方である。この山はまた、等高線（等ポテンシャル線とよぶ）をxy面に描くことにしても表現できる（z＝0に限定しなければ等ポテンシャル「面」で表現することになる）。ポテンシャルの山は、もとの力の場も表現している。実際、質点mを等ポテンシャル線に沿って運ぶのに仕事は不要だから、図Bの(2)の点Pで質点mに働く力は等ポテンシャル線に沿う成分をもたないことが、まずわかる。力は等ポテンシャル線に垂直な成分をもつのみだから、その成分をf(P)と書いてみる。質点mを静かに山の上方の点P'まで引き上げるには、質点に－f(P)の力を加えるので、－f(P)・PP'だけの仕事をすることになる。これがポテンシャルの増加
　　W(P')－W(P)
になるわけだから、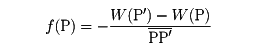

が導かれる（正確にはP'→Pの極限をとる）。つまり力は、ポテンシャルの山からその勾配(こうばい)として求められる。このことは、いま考えた電荷の間の力に限らず一般にいえる。

［江沢　洋］

『戸田盛和著『物理入門コース1　力学』（1982・岩波書店）』▽『原島鮮著『質点の力学』改訂版（1984・裳華房）』▽『S・ガシオロウィッツ著、林武美・北門新作訳『量子力学1』（1998・丸善）』▽『江沢洋著『量子力学1、2』（2002・裳華房）』▽『江沢洋著『力学――高校生・大学生のために』（2005・日本評論社）』

[参照項目] | 位置エネルギー | 場

力の場とポテンシャル〔図A〕

ポテンシャルの場の表し方〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

ポテンシャル

ベクトルVの場が渦なし，つまりいたるところでVの回転rot Vが０であれば，VをあるスカラーΦの勾配(こうばい)としてV＝grad Φの形に表すことができ，このΦをVのスカラーポテンシャルまたは単にポテンシャルという。ベクトル場よりも数学的扱いが簡単なためよく用いられる。Φ＝一定の面（等ポテンシャル面）はその上の各点におけるベクトルに直交する。ベクトルが流体の速度，力，静電場，磁場のとき，それらのポテンシャルを速度ポテンシャル，位置エネルギー，電位，磁位という。ポテンシャルの概念はさらに拡張されて，電磁場のベクトルポテンシャルや，熱力学的ポテンシャル，化学ポテンシャル等も定義されている。

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

ポテンシャル
potential

位置エネルギーは保存力場内にある質点の仕事をする能力を表わすが，この能力を保存力場そのものが潜在的にもつと考えるときに，位置エネルギーを力場のポテンシャルという。ポテンシャル U(x，y，z) はスカラー量であって，保存力 F の成分は F_x＝－∂U/∂x，F_y＝－∂U/∂y，F_z＝－∂U/∂z で与えられる。この3式の和を F＝－gradU と書き，右辺を U の負の勾配という。静電気力は保存力であって，静電ポテンシャルは電位とも呼ばれる。

出典　ブリタニカ国際大百科事典 小項目事典

DBM用語辞典

ポテンシャル【potential】

ポテンシャルは、製品・商品あるいはサービスの市場性・市場規模である。どこに市場があり、その市場規模はどれほどの可能性を持つかを検討する。すでに販売している製品・商品、サービスなら、成長市場にあるのか、成熟市場にあるのか、それとも停滞市場にあるのかを想定しながら、その市場規模を検討する。ポテンシャルは9Pのひとつ。

出典　(株)ジェリコ・コンサルティング

流通用語辞典

ポテンシャル【potential】

ポテンシャルは、製品・商品あるいはサービスの市場性・市場規模である。どこに市場があり、その市場規模はどれほどの可能性を持つかを検討する。すでに販売している製品・商品、サービスなら、成長市場にあるのか、成熟市場にあるのか、それとも停滞市場にあるのかを想定しながら、その市場規模を検討する。ポテンシャルは9Pのひとつ。

出典　(株)ジェリコ・コンサルティング

世界大百科事典（旧版）内のポテンシャルの言及

【ベクトル解析】より

…このときFは局所的には，スカラー関数φを使ってF＝gradφと表される。φをFのポテンシャルpotentialという。divF＝0なるベクトル場Fはわき出しなし，あるいはソレノイダル(管状)であるという。…

【ポテンシャル論】より

…ベクトル場FがスカラーUによってF＝－gradUと表されるとき，UをFのポテンシャルという。　例えば，三次元空間の，集合Eを占める物体Mがあり，点Q∈Eにおける密度がρ(Q)のとき，万有引力の定数をGとおけば，物体Mによる重力の場Fは，ポテンシャル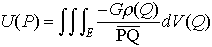，の－gradUに等しい。…

※「ポテンシャル」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」