精選版 日本国語大辞典 「リーマン幾何学」の意味・読み・例文・類語
リーマン‐きかがく【リーマン幾何学】
改訂新版 世界大百科事典 「リーマン幾何学」の意味・わかりやすい解説
リーマン幾何学 (リーマンきかがく)
Riemannian geometry
微分幾何学とリーマン幾何学との間の境界は必ずしも明りょうではないが,リーマン幾何学は一応はリーマン多様体の上で行われる微分幾何学であるということができる。リーマン多様体を特徴づけるものはリーマン計量(gij)であるから,リーマン幾何学の特徴もまた,リーマン計量から導かれる種々の概念と,その研究であるということになろう。したがって,リーマン幾何学における研究対象として,第1に距離,面積などの計量概念をあげることができる。これは,リーマン多様体上に与えた曲線なり曲面なりの微小部分を接空間の中へ移してみれば,リーマン計量ないし,それが定める接空間内の内積によって,この微小部分に長さ,面積を対応させることができ,それを積分することによって初めに与えた曲線,曲面の長さ,面積を定めることが可能になるからである。さらにこの長さを利用して2点間の距離を,それらを結ぶ曲線の長さの最小値(正式には下限)と定めることができる。この距離を保つようなリーマン多様体の間の写像を等長写像というので,形式的にはリーマン幾何学は等長写像によって不変な性質概念を研究するものであると定義することもできる。先にあげた,長さ,面積を曲線や曲面の集合の上の関数とみたとき,それらの極値を与える曲線,曲面は,したがってリーマン幾何学の研究対象であり,それぞれ,測地線,極小曲面と呼ばれている。ただし,これら測地線論,極小曲面論は,その研究に利用される方法論が,あるいはモース理論を通じて位相幾何学に及び,あるいは,偏微分方程式論にも及ぶために,それらを単純なリーマン幾何学の一分野とみなすことは多少の無理が生ずる場合も起こりうる。よりふつうに,リーマン幾何学と呼ばれるものは,リーマン計量から導かれる接続,平行性を研究対象とするものである。これらは,一般の微分可能多様体の上に形式的に定められる接続,平行性などに比べてよりユークリッド空間のそれに近い自然な性質をもち,リーマン接続(またはユークリッド接続),T.レビ-チビタの平行性の名で知られている。これらおよびそれの定める共変微分の研究には,テンソル解析が援用されることも多いが,その援用を容易ならしめるのが,リーマン計量を利用して行われる指標(添字)の上げ下げである。これは,接空間に(gij)による内積〈 〉が与えられたことによって可能になるベクトルX=(Xi)から,一次写像L(X)への移行,式では,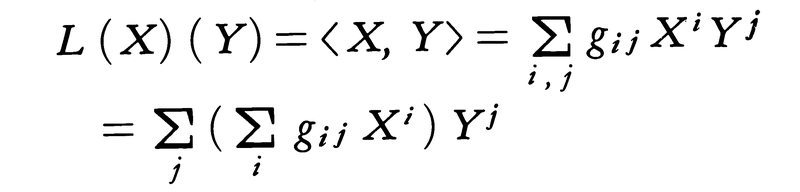
を,上に添字をもつベクトルX=(Xi)から,下に添字をもつベクトル(Xj),Xj=ΣgijXiへの移行と読みかえる操作を拡大したものにほかならない。(gij)の逆行列(gij)によってこの逆の操作も可能であり,したがって一般にテンソル(Rabc),……に対しても(gij),(gkl)を適当に乗じて和をとれば,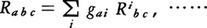 のように,添字を上げ下げすることは自由である。この手法を使って調和積分論でも使われるラプラス=ベルトラミ作用素などを共変微分によって書き下すことも可能になる。さて,測地線論,調和積分論においてもみられるように,リーマン幾何学の研究の最初に現れる対象が,結局はリーマン多様体の位相幾何学的性質を反映しているということも多く,この方向の研究も現在盛んに行われる。例えば,古くから知られたガウス=ボンネの定理は,曲率という微分幾何学的量と,オイラー数という位相幾何学的量との橋渡しであると考えることができ,現在では,(微分幾何学的)特性類理論としての再構成が行われている。一方,それとは少し異なるが,リーマン多様体のそれ自身への等長写像は等長変換群という群を作るので,この群の構造から逆に,もとのリーマン多様体の構造を探ることも行われる。この方向の一つは,等質空間論として展開され,リー群論の特有の手法のリーマン幾何学への応用を可能にしてきている。このように,リーマン幾何学は,単にリーマン多様体の幾何学というに止まらない面を有しており,その目的,手法によって,他分野の数学の色彩をおびることも多いようである。
のように,添字を上げ下げすることは自由である。この手法を使って調和積分論でも使われるラプラス=ベルトラミ作用素などを共変微分によって書き下すことも可能になる。さて,測地線論,調和積分論においてもみられるように,リーマン幾何学の研究の最初に現れる対象が,結局はリーマン多様体の位相幾何学的性質を反映しているということも多く,この方向の研究も現在盛んに行われる。例えば,古くから知られたガウス=ボンネの定理は,曲率という微分幾何学的量と,オイラー数という位相幾何学的量との橋渡しであると考えることができ,現在では,(微分幾何学的)特性類理論としての再構成が行われている。一方,それとは少し異なるが,リーマン多様体のそれ自身への等長写像は等長変換群という群を作るので,この群の構造から逆に,もとのリーマン多様体の構造を探ることも行われる。この方向の一つは,等質空間論として展開され,リー群論の特有の手法のリーマン幾何学への応用を可能にしてきている。このように,リーマン幾何学は,単にリーマン多様体の幾何学というに止まらない面を有しており,その目的,手法によって,他分野の数学の色彩をおびることも多いようである。
執筆者:四方 義啓
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「リーマン幾何学」の意味・わかりやすい解説
リーマン幾何学
りーまんきかがく
Riemannian geometry
リーマン多様体、すなわちリーマン計量が与えられた可微分多様体の微分幾何学をいう。可微分多様体の各点における接空間に内積を対応させる可微分写像をリーマン計量という。内積が与えられることにより各接空間はユークリッド空間の構造をもつから、リーマン幾何学はユークリッド幾何学を一次近似にもつ幾何学といえる。内積が与えられたベクトル空間(すなわちユークリッド空間)はもっとも簡単なリーマン多様体であるから、リーマン幾何学はユークリッド幾何学の一般化である。また、空間内の曲面の第一基本形式はリーマン計量であり、曲面上で第一基本形式だけで決まる性質を研究する幾何学はリーマン幾何学の重要な例である。
可微分多様体上にリーマン計量が与えられれば曲線の長さを測ることができるから、2点を結ぶ(局所)最短線を考えることができる。これを測地線といい、ユークリッド幾何学における直線の一般化である。また、ユークリッド空間における平行移動の概念をリーマン多様体に一般化することができ、それに基づいて共変微分とよばれる微分演算が定義される。これはベクトル場の微分がまたベクトル場であるような微分演算である。
リーマン多様体Mの点Pにおいて平面(接空間の二次元部分空間)πが与えられたとき、Pを通りπに接する測地線全体によって張られる曲面のガウス曲率を、MのPにおける断面曲率という。断面曲率が一定であるようなリーマン多様体を定曲率空間という。単連結で完備な定曲率空間はユークリッド空間、球面、双曲空間の3種類である。球面および双曲空間におけるリーマン幾何学が非ユークリッド幾何学にほかならない。
リーマン計量を変えない(すなわち2点間の距離を変えない)変換を等長変換という。等長変換の全体はリー群をつくり等長変換群といわれる。定曲率空間は最大の等長変換群をもつリーマン多様体である。各点を中心とする点対称変換が等長変換であるようなリーマン多様体を対称空間という。定曲率空間は対称空間であるが、それ以外にも多くの対称空間が存在する。対称空間には等長変換群が推移的に作用しているから等質空間である。一つの方向を含み互いに直交するすべての断面に関する断面曲率の平均をリッチ曲率といい、リッチ曲率が一定であるようなリーマン多様体をアインシュタイン空間という。対称空間は完全に分類されているが、アインシュタイン空間については、いまだわからない性質が多い。
[荻上紘一]
百科事典マイペディア 「リーマン幾何学」の意味・わかりやすい解説
リーマン幾何学【リーマンきかがく】
→関連項目幾何学|測地線|リーマン予想
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「リーマン幾何学」の意味・わかりやすい解説
リーマン幾何学
リーマンきかがく
Riemannian geometry
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内のリーマン幾何学の言及
【幾何学】より
…20世紀に入ると,クラインの思想の影響を受けて,射影空間の曲線や曲面の射影変換で不変な性質を微分学を用いて研究する射影微分幾何学がフビニG.Fubiniらによって研究され,その他のいろいろな空間に対しても同様の微分幾何学がブラシュケW.Blaschke(1885‐1962)らによって研究された。
[リーマン幾何学]
媒介変数u,vを用いて表された曲面上の無限に近い2点,すなわち(u,v)と(u+du,v+dv)に対応する曲面上の2点間の距離dsは,ds2=Edu2+2Fdudv+Gdv2という形で与えられる。ここにE,F,Gはu,vに関して連続的微分可能なある関数である。…
【相対性理論】より
…これは,先に述べた単純な等価原理,つまり慣性質量と重力質量の等価性よりもさらに一般的な等価原理の表現であり,これをアインシュタインは一般相対性理論を作る際の物理的な柱とした。
[リーマン幾何学と一般相対性理論]
次にもう少し数学的な面に移ろう。特殊相対性理論で考える時空はミンコフスキー空間であった。…
※「リーマン幾何学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

