測地線（読み）ソクチセン（英語表記）geodesic

デジタル大辞泉

そくち‐せん【測地線】

曲面上で二点間を結ぶ曲線のうち、最短距離のもの。球面上では大円の弧。

出典　小学館

精選版 日本国語大辞典

そくち‐せん【測地線】

1. 〘 名詞 〙 ある曲面上の二点間の最短距離。測地曲線。〔自然科学的世界像（1938）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

測地線 (そくちせん)
geodesic

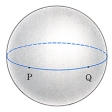
直線の概念を多様体に対して拡張したものであって，2点を結ぶ曲線のうちで，その長さが極値的になっているものをいう。直線の場合は上の〈極値的〉が〈最短〉におきかえられているわけである。ここで極値的とは変分法における用語であって，微積分学における極値と同じく，ごく近い曲線とその長さを比較するとき，ほとんどその増減が認められないこと，すなわち第1変分が0であることをいう。測地線は，したがって変分法の基本方程式であるオイラー=ラグランジュの微分方程式によっても書き表される。測地線は局所的には直線に似た性質をもつ。すなわち多様体についてもごく小さいある種の近傍にかぎればその2点を結ぶその中の測地線はただ1本存在しかつ最短である。しかし大域的には次の球面の例からも知られるように一意とはかぎらないし，最短でもない。すなわち球面の2点を結ぶ測地線は，それらを通る大円の小弧でもあり，大弧でも，さらに一般にはその大円を任意回まわったうえで一方から他方に到達するものでもあるからである。
執筆者：四方 義啓

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

測地線
そくちせん

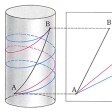
曲面上の曲線で、その十分小さい任意な部分が、2点を結ぶ最短線であるようなものをいう。測地線は平面上の直線の一般化である。球面の測地線は大円であるから閉曲線で一定の長さをもつ。直円柱面の測地線は母線と平行円とつるまき線（常螺線(らせん)）であり、平行円のみが閉曲線である。一般の回転面の測地線をすべて求めるのはむずかしいが、子午線と平行円が測地線であることは容易にわかる。

　直線はそのいかなる部分をとっても2点を結ぶ最短線であるが、この性質は一般の曲面上の測地線に対して成り立たない。たとえば、球面上では大円上の2点に対して劣弧は最短線であるが、優弧は最短線ではない。また、平面上では2点を通る直線はただ1本であるが、この性質も一般の曲面上の測地線に対しては成り立たない。球面では対心点を通る測地線は無数に存在し、直円柱面では同一円上にない2点を通る測地線は無数に存在する。しかし十分小さな範囲内では2点を通る測地線はただ1本である。測地線は空間内の曲面に対してのみならず、一般のリーマン多様体においてまったく同様に定義される。

［荻上紘一］

[参照項目] | リーマン幾何学

測地線（球面の大円上の2点に対する最短…

測地線（球面の対心点を通る測地線）

測地線（直円柱面における同一円上にない…

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

測地線【そくちせん】

曲面上（一般にはリーマン空間（リーマン幾何学）内）の任意の２点を結ぶ曲線のうち，長さが最も短い（ときには最も長い）もの。平面上では直線，球面上では大円の弧。一般相対性理論では，万有引力場内の質点の運動や光線の経路は，ゆがんだ４次元時空間内（四次元世界）の測地線で表される。

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

測地線
そくちせん
geodesic line

空間内または曲面上の2点を結ぶ最短距離の曲線。平面上またはユークリッド空間内では直線であり，三次元球面上では大円となる。物理学では測地線は真空中の2点を通る光の経路で，特殊相対性理論の範囲では直線であるが，一般相対性理論では曲線となる。 (→測地的曲率 )

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の測地線の言及

【相対性理論】より

…これからのずれが重力を表す。重力のために曲がった時空の中で質点は(他の力がなければ)測地線に沿って動く。測地線とは，2点を結ぶ最短の曲線で，球面の例でいえば大円がこれである。…

※「測地線」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」