ルベーグ積分（読み）ルベーグセキブン（英語表記）Lebesgue integral

デジタル大辞泉

ルベーグ‐せきぶん【ルベーグ積分】

通常の積分での面積や体積の代わりに、ルベーグ測度とよぶ面積や体積を拡張した概念を用いて定義した積分。通常の積分よりも適用範囲が広い。フランスの数学者ルベーグ（H.Lebesgue）が創始。

出典　小学館

精選版 日本国語大辞典

ルベーグ‐せきぶん【ルベーグ積分】

1. 〘 名詞 〙 ( ルベーグは Lebesgue フランスの数学者の名から ) Ｈ=ルベーグの発見した積分の概念。通常の積分よりも多くの関数を積分できるなどはるかに便利で強力なので、現代数学でよく用いられる。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

ルベーグ積分
るべーぐせきぶん
Lebesgue integral

普通、微積分学の教科書に出てくる積分はリーマン積分とよばれるもので、定義は簡単であるが、いくつかの欠点をもっている。たとえば、積分可能な関数列｛f_n(x)｝が、各点xでf(x)に収束しても、f(x)が積分可能でなかったり、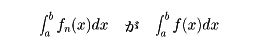

に収束しなかったりすることである。また、二変数の関数f(x,y)の積分順序の変換に、積分と関係のない連続性などの条件が必要になったりする。

　ルベーグは1902年の学位論文で、これらの欠点を除き、しかも、リーマン積分可能な関数の積分の値は同じになるような積分を構成した。これがルベーグ積分とよばれているもので、近代解析学の基礎として不可欠のものとなっている。ただし、ルベーグ積分の構成法はやや複雑であり、いろいろ改良した流儀があるが、いずれも同じ積分に帰着する。

　抽象的に、測度空間(X,M,m)を考える。すなわち、集合Xの部分集合の族Mで、集合E∈Mには測度m(E)が定義され、これが完全加法的な測度になっているとする。このときMの要素である集合を可測集合という。

　X上の実数値関数f(x)が、任意の実数αに対し、集合
　　｛x∈X;f(x)＞α｝∈M（可測集合）
となるとき、この関数を可測関数という。可測関数f(x)に対し、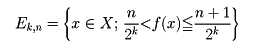

と置けば、E_k,n∈Mであるから

が確定するとき、関数f(x)は積分可能となる。この極限値を関数f(x)の測定空間(X,M,m)上のルベーグ積分といい、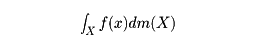

で表す。また、積分可能な関数の集合をL¹(X,M,m)または簡単にL¹で表す。とくにXがn次元ユークリッド空間Rⁿで、Eが区間のとき、mが区間Eの体積|E|を表すならば、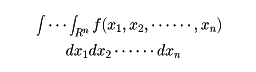

と表す。

　ルベーグ積分の代表的な特性をいくつかあげると、
（1）関数f(x)が可測で、ある積分可能な関数g(x)があって、|f(x)|≦g(x)ならば、f(x)も積分可能となる。

（2）｛f_n(x)｝⊂L¹(X,M,m),f_n(x)→f(x)、しかも|f_n(x)|≦g(x)∈L¹(X,M,m)ならばf(x)∈L¹(X,M,m)となり、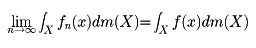

これは積分とlimが交換可能であることを示している。これをルベーグの収束定理という。

（3）二変数の関数f(x,y)∈L¹(X,M,m)ならば、重積分は繰り返し積分となり、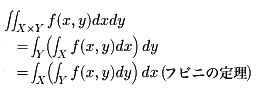

（4）測度空間(X,M,m)上の可測関数f(x)で、

となる関数f(x)の集合をL^p(X,M,m)とし、これにノルムを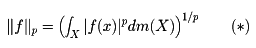

で定義すると、L^p(X,M,m)はバナッハ空間となる。とくに、p=2のときはヒルベルト空間である（リース‐フィッシャーの定理）。

　このように、ルベーグ積分によって関数解析に役だつ関数空間がつくられた（リーマン積分可能な関数に、リーマン積分により、式（＊）でノルムを定義しても完備にはならない）。

［洲之内治男］

『伊藤清三著『ルベーグ積分入門』（1963・裳華房）』▽『洲之内治男著『ルベーグ積分入門』（1974・内田老鶴圃）』

[参照項目] | 測度

ルベーグ積分

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ルベーグ積分 (ルベーグせきぶん)
Lebesgue integral

初等微積分において学ぶふつうの積分は，19世紀中ごろにG.F.B.リーマンによって現代的に厳密な定義が与えられたのでリーマン積分と呼ばれ，連続関数の積分に関するかぎりほぼ完全なものであるが，解析学でしばしば現れる極限操作については不十分な点がある。例えば，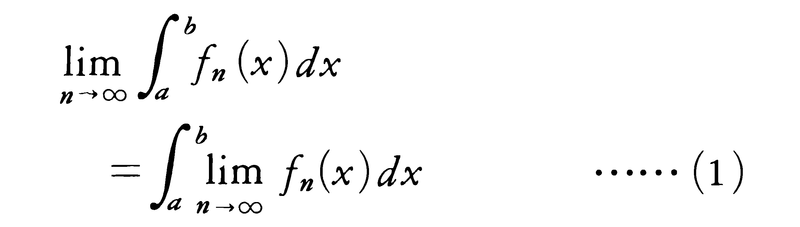

が成り立つためには，関数列｛f_n（x）｝が区間［a，b］で一様収束するというようなかなり強い仮定が必要である。この難点を克服したのが，20世紀初めにH.ルベーグによって創始された測度の概念に基づくルベーグ積分である。一般にn次元ユークリッド空間Rⁿにおいて，区間（座標平面に平行な面をもつn次元直方体）Iのn次元体積を｜I｜と書く。集合E⊂Rⁿを区間の可算無限列｛I_ν｝でおおい，そのようなあらゆるおおい方に対する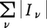の下限をm^＊（E）と書いて，Eの外測度という。任意の集合A⊂Rⁿに対して，

　m^＊（A）＝m^＊（A∩E）＋m^＊（AE）

となるときEは可測（ルベーグ可測）であるといい，m^＊（E）を単にm（E）と書いてEの測度，またはルベーグ測度という。可算無限個の集合E₁，E₂，……，E_n，……が可測ならばそれらの和集合も可測であり，とくに｛E_ν｝がどの二つも互いに交わらないならば，可算加法性，

が成り立つ。測度はふつうのn次元体積の概念の拡張であるが，ふつうのn次元体積では（2）は有限個の集合に対してのみ成り立つのに対して，測度では可算無限個の集合の列に対して（2）が成り立つ点がすぐれている。リーマン積分がふつうの体積の概念に立脚しているのに対して，測度の概念に立脚して構成される積分がルベーグ積分である。現代では，もっと一般の空間において測度と積分の理論が構成されているので，そのような理論を積分論といい，ルベーグ積分はその中に含まれている。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ルベーグ積分
ルベーグせきぶん
Lebesgue's integral

f(x) を区間 [a，b] で定義された有界な関数として，まず f(x)≧0 の場合を考える。 [a，b] における f(x) の下限を L ，上限を M とし，区間 [L，M] を分点 L＝α₀＜α₁＜α₂＜…＜α_n-1＜α_n＝M で n 個の小区間に分割し，この分割を Δ とする。 α_i≦f(x)≦α_i+1 となるような x の集合の測度を m(α_i，α_i+1) とし

，

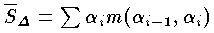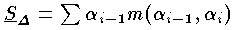
とおけば，α_i－α_i-1 の最大のものが0に近づくように分割 Δ を細くしたとき 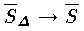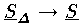， となる。このとき，もし 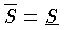であればその共通の値 S を f(x) の a から b までのルベーグ積分という。積分をこのように定義すると，不連続関数も積分可能になりやすく，しかも積分可能な関数のつくる関数空間が完備になるので，関数解析に都合がよい。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

ルベーグ積分【ルベーグせきぶん】

ある区間で定義された有界な関数に対し通常の積分（リーマン積分）が可能であるためには，関数がその区間で連続であるか，不連続点があっても有限個でなければならない。しかし1902年ルベーグは積分の概念を拡張して，さらに広範囲の関数に対しても積分が定義できるようにした。これをルベーグ積分といい，リーマン積分よりすぐれた点があるため，今日の数学で広く用いられる。
→関連項目実変数関数論｜積分

出典　株式会社平凡社

世界大百科事典（旧版）内のルベーグ積分の言及

【解析学】より

…すなわち，P.ディリクレはフーリエ級数に関する二つの論文(1829,37)において，関数の現代的な定義を確立したが，その後リーマンが積分の一般的な定義を確立(1854)し，G.カントルが無理数論および集合論を創始した(1872)のも，フーリエ級数が誘因の一つであったと思われる。さらに20世紀の初めに，H.ルベーグは彼の名を冠した測度の概念を導入し，それをもとにしたルベーグ積分の理論を創始した。実関数論はルベーグ積分論を核として発展し，フーリエ級数やフーリエ解析における多くの著しい結果が得られているが，ルベーグ積分論は，後に述べる関数解析学においても基本的な役割を演じ，欠くことのできない理論である。…

【実関数論】より

…彼は直線上の図形の長さ，平面図形の面積，空間図形の体積の概念を，できるだけ一般な図形の範囲に拡張することを考え，測度という概念を導入し，それをもとにして積分の理論を展開した。この測度が彼の名を冠して呼ばれるルベーグ測度であり，ルベーグ測度をもとにして構成される積分がルベーグ積分である。ルベーグ積分はリーマン積分の拡張であるばかりでなく，リーマン積分と比べて多くの利点がある。…

【測度】より

…この測度を現在ではルベーグ測度と呼ぶ。このような測度の概念を用いて定義される積分をルベーグ積分という。ルベーグ積分においては，測度の可算加法性のおかげで，従来の面積や体積を用いて定義された積分(リーマン積分)よりも極限操作などがはるかに容易になり，ルベーグ積分論は20世紀の解析学に目覚ましい発展をもたらした。…

※「ルベーグ積分」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」