多項式環（読み）たこうしきかん（英語表記）polynomial ring

改訂新版　世界大百科事典

多項式環 (たこうしきかん)
polynomial ring

単位元1をもつ可換環R上のx₁，x₂，……，x_nの多項式全体をR［x₁，……，x_n］で表す。多項式の和，積でR［x₁，……，x_n］の和，積を定めると，R［x₁，……，x_n］は単位元をもつ可換環になる。この環をR上のn変数多項式環という。

　Rから可換環Aへの環準同型φで，φ（1）がAの単位元になっているものが与えられているとき，A（正確にはAとφの組）はR-代数であるという。R-代数（A，φ）から（A′，φ′）への環準同型ψが，Rの任意の元rについて，ψφ（r）＝φ′（r）という性質をもつとき，R-代数の準同型であるという。R-代数（A，φ）について，φ（R）はAの部分環である。Aの元a₁，……，a_nとφ（R）がAの中で生成する部分環をR［a₁，……，a_n］で表す。とくに，R［a₁，……，a_n］＝Aとなるa₁，……，a_nが存在するとき，AはR上有限生成であるといい，a₁，……，a_nはR上Aを生成するという。多項式環R［x₁，……，x_n］は有限生成なR-代数であり，x₁，……，x_nはR上R［x₁，……，x_n］を生成する。A＝R［a₁，……，a_n］のとき，R［x₁，……，x_n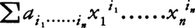］の元，にAの元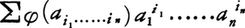，を対応させる写像をδとすると，δは多項式環R［x₁，……，x_n］からAの上へのR-代数の準同型である。δの核δ⁻¹（0）＝｛f（x₁，……，x_n）∈R［x₁，……，x_n］｜δ（f（x₁，……，x_n））＝0｝はR［x₁，……，x_n］のイデアルであり，準同型定理によれば，Aは剰余環R［x₁，……，x_n］/δ⁻¹（0）に同型になる。このように，R上有限生成なR-代数はすべてR上の多項式環の準同型像として表される。

　多項式環R［x₁，……，x_n］を考える。多項式f（x₁，……，x_n）が二つの定数でない（Rの元でない）多項式の積に因数分解されるとき，f（x₁，……，x_n）は可約であるという。可約でない多項式（すなわち，f（x₁，……，x_n）＝g（x₁，……，x_n）h（x₁，……，x_n）ならばg（x₁，……，x_n），h（x₁，……，x_n）の一方はRの元）は既約多項式と呼ばれる。ある多項式が既約であるかどうかはRの取り方による。例えば，x₁²－2x₂²は有理数体Q上では既約であるが，実数体R上では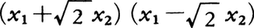と分解する。かってなQ［x₁，……，x_n］の元f（x₁，……，x_n）は既約な多項式の積に因数分解する。また，この分解は各因子にQの元をかけることを除いて一意的である。この性質は体を係数域にもつ多項式環で成り立つ。このような性質をもつ環のことを素元分解環（unique factorization domain。略してUFD）と呼ぶ。

　代数幾何学の大きな目標は，体K上のアフィン空間Kⁿ＝｛（a₁，……，a_n）｜a_i∈K｝の中で，多項式f₁（x₁，……，x_n），……，f_r（x₁，……，x_n）の共通零点V（f₁，……，f_r）＝｛（a₁，……，a_n）∈Kⁿ｜f₁（a₁，……，a_n）＝……＝f_r（a₁，……，a_n）＝0｝を研究することである。f₁，……，f_rがK［x₁，……，x_n］の中で生成するイデアルIを取ると，K［x₁，……，x_n］/IがV（f₁，……，f_r）を調べるうえで本質的役割を果たす。したがって，K上有限生成なK-代数，とくにK［x₁，……，x_n］は代数幾何学において基本的なものである。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

多項式環
たこうしきかん

実数を係数とするxの多項式の考えを一般化して、可換体kと文字xに対して
　　a₀xⁿ+a₁x^n-1+……+a_n
という形の式をk上xの多項式という。k上xの多項式全体をk［x］で表し、このk［x］をk上の多項式環という。多項式に対しては通常の方法で和と積が定義され、k［x］は可換環になる。

　多項式環の理論のなかで重要なのは、既約な多項式への分解への一意性の定理である。可換体k上の多項式f(x)が、同じくk上の多項式g(x),h(x)によって
（1）f(x)=g(x)h(x)と表される
（2）g(x),h(x)はf(x)より低次数
であるとき、f(x)はk上可約であるといわれ、（1）、（2）のようにはできないとき、k上既約であるといわれる。

　多項式環における既約な多項式は、整数環における素数のようなものである。整数の場合に「任意の整数は素数の累乗の積の形に一意的に表される」（たとえば100=2²×5²）ように、「任意の多項式は既約多項式の累乗の形に一意的に表される」ことが証明され、これが代数方程式の理論の基礎となっている。

　さらにk上の有理式とは、k上の多項式f(x),g(x)（ただしg(x)≠0）に対してf(x)/g(x)と表される式のことである。可換体k上の有理式の全体はまた一つの可換体であり、これを有理関数体という。

［寺田文行］

[参照項目] | 代数方程式

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

多項式環
たこうしきかん
polynomial ring

R を可換環とするとき，R の元 a₀，a₁，…，a_n-1，a_n を係数とする変数（あるいは文字，記号）の多項式 f(x)＝a₀xⁿ＋a₁x^n-1＋…＋a_n-1x＋a_n の全体は，通常の加法および乗法に関して環をつくる。これを x に関する R の上の多項式環といい，R[x]と書く。x を多項式環の不定元ということがある。一般に n 個の不定元 x₁，x₂，…，x_n について R[x₁，x₂，…，x_n]が生成される。

出典　ブリタニカ国際大百科事典 小項目事典