天元術（読み）テンゲンジュツ（英語表記）Tiān yuán shù

デジタル大辞泉

てんげん‐じゅつ【天元術】

算木さんぎを用いて高次方程式を解く高等の和算。中国の宋・元の時代に起こった代数学が日本に渡来したもので、未知数のことを天元の一と称した。今の開平・開立の類。

出典　小学館

精選版 日本国語大辞典

てんげん‐じゅつ【天元術】

1. 〘 名詞 〙 算木(さんぎ)を用いて高次の方程式を表わし、これを解く一種の代数。一三世紀、中国の宋・元の頃発生したもので、縦横の区画をもつ算盤(さんばん)の上に算木を並べて、方程式を立て、その算木を動かして方程式の根(こん)を計算した。一七世紀、日本に伝来してから、開平・開立などの計算も行なわれるようになった。未知数を表わす一本の算木を盤上の一定の位置に置き、これを「天元の一」と呼んだところからの名称という。天元。
   1. [初出の実例]「算法根源記四冊 佐藤利左衛門尉正興著 〈略〉其施す所の術を見れば、天元術は不_レ好と見へて」(出典：算法古今通覧（1797）一)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

天元術 (てんげんじゅつ)
Tiān yuán shù

中国で発達した一種の代数学。中国数学では算木を使って数字を表し，各種の計算を行った。金がモンゴルに滅ぼされた1234年のころ華北の地で考案された天元術は，これに加えて未知数を表示し，代数計算を行った。現在の代数で〈未知数をxとする〉という表現に対し，天元術では〈天元の一を立てる〉といい，これがその名称の起りである。算木による数字をアラビア数字で表すと，例えば25x²＋280x－6905は，

　　　　25

　　　 280　元

　　－6905

のように〈元〉字を添えることによって表示された。天元術に関する現存最古の数学書は金の李冶の《測円海鏡》（1248）である。元の時代に朱世傑は《算学啓蒙》（1299）を著して天元術を解説した。この書物は朝鮮で復刻され，これが豊臣秀吉の文禄・慶長の役のころ日本に伝わり，和算の発達に大きな影響を与えた。
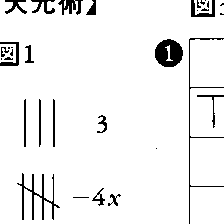
執筆者：藪内 清　日本に天元術が伝わったのは，中国の《算学啓蒙》を江戸初期の数学者が読んで理解することができたからである。とくに研究は関西の数学者から始まった。橋本正数の弟子の沢口一之は，その著《古今算法記》（1671）の中で天元術を解説した。算木は朱が正の数，黒が負の数を表す。紙に書くときは，負の数には斜めに筋を入れる。図1は3－4x＋x²－7x³，あるいはこの式が0に等しいことを表す。前述の〈天元の一を立てる〉とは，図2に示す0＋1・xのことである。次に図3に天元術による解き方を示す。例えば，面積644歩の長方形があって，横は縦より5間短いとする。横の長さを天元の一，すなわち未知数xとおく。方程式はx²＋5x－644＝0が得られる。まず，x²－644≒0とみて，x₁＝20を得る。x²＋5x－644＝（x－20）（x＋25）－144＝（x－20）²＋45（x－20）－144，ここでx₂＝x－20とおく。x₂²＋45x₂－144＝（x₂－3）（x₂＋48）であるから，x₂＝3が得られる。したがって，x＝x₁＋x₂＝20＋3＝23が答えである。

　関孝和は，この天元術を一般的な代数に応用し，紙に書き表せるように改良した。これが点竄（てんざん）術である。関の時代には分数式の表し方に苦労したが，関の弟子建部賢弘により，今日の方法とほぼ同じ方法がくふうされた（図4）。
執筆者：下平 和夫

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

天元術
てんげんじゅつ

中国および日本で中世に行われた用器式代数をいう。中国において朱世傑(しゅせいけつ)が『算学啓蒙(けいもう)』（1299）で初めて用いた、赤黒の算木（赤は正数、黒は負数を表す）を用い、それを升目を引いた算盤の上に並べて一元の高次方程式を表し問題を解いた。ただこの方法の発明された時期がそろばんの流行期と重なったため、まもなく算木の使用が廃れ、同時に天元術も廃れてしまった。隣国朝鮮では後世に至るまで算木が用いられ、豊臣(とよとみ)秀吉の朝鮮侵略を機会として日本に伝わり天元術が行われることになった。

　点竄(てんざん)術が始まると天元術は不用となるわけであるが、点竄術を学ぶ予備段階として初学者の間で行われた。そのため『改正天元指南』などの書物の流行は続いた。

　天元術の名は、未知数のことを天元の一と称し、○○を未知数とするという意味を「天元の一を立てて○○とする」という言い方をすることから出たものであって、中国では天元のほかに、人元、地元などの未知数をいくつか用いた四元法なども行われたが、これは流行をみないで終わった。

［大矢真一］

[参照項目] | 点竄術

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

天元術【てんげんじゅつ】

13世紀ごろ中国で発達した代数学。未知数xを〈天元之一〉と名づけたところからこう呼ばれた。未知数を含む代数方程式を立て，算木を用いて解くことにより多くの応用問題を扱った。李冶の《測円海鏡》，朱世傑の《算学啓蒙》等に紹介されたが，そろばんの普及により算木の使用がすたれるとともに中国では滅びた。日本には文禄・慶長の役ごろ伝わり，江戸時代初期に普及。しかし多くの未知数や，整数でない指数を扱えない欠点があり，点竄(てんざん)術の発明により衰微。
→関連項目和算

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

天元術
てんげんじゅつ
tian-yuan-shu

未知数を使って方程式をつくり，算木を並べて未知数の値を求める計算法。すでに『九章算術』には2元や3元の1次連立方程式や1元2次方程式が取扱われていたが，天元術に関する最古の著述は，李治の『測円海鏡』 (1248) である。李治の『益古演段』 (59) は，蒋周の『益古集』に基づいた天元術を論じた。元という文字によって未知数を表わし，「天元の一を立てる」という表現は，未知数を xとするという意味であった。そこから立天元一術とか天元術という名称が起った。代数計算を自由に行い，同時に負の次数をもった式の表示や計算も実行された。日本では江戸時代に朱世傑の『算学啓蒙』 (99) によって天元術が知られ，そこから点竄 (てんざん) 術が生れた。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の天元術の言及

【中国数学】より

…この金･元交替のころ，華北を中心に新しい数学が興った。かつて金に仕えた李冶の《測円海鏡》(1248)に紹介された〈天元術〉がそれで，一種の代数術である。現在の代数学で〈未知数をxとする〉というのに対し，〈天元の一を立てる〉といい，〈元〉字を数字の横に記し，任意の次数の方程式を表示するのである。…

※「天元術」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」