対偶（読み）タイグウ

デジタル大辞泉

たい‐ぐう【対偶】

１ 二つで組みになっているもの。対つい。
「この線は、鬢びんの下端の線などと目立った―をしている」〈寅彦・浮世絵の曲線〉
２ 対句ついく。
３ 論理学で、「pならばqである」に対して、仮定および結論を否定し同時に両者を逆にした「qでなければpでない」という形の命題。原命題が真ならば、その対偶も必ず真となる。→裏 →逆

出典　小学館

精選版 日本国語大辞典

たい‐ぐう【対偶】

1. 〘 名詞 〙
2. ① ( ━する ) 二つで一そろいになっていること。つい。
   1. [初出の実例]「当は対偶している事ぢゃが、夫婦にえなるまいと恐るるぞ」(出典：寛永刊本蒙求抄（1529頃）六)
   2. 「此雲の変幻出没と彼水の寂静不動と対偶す」(出典：日本風景論（1894）〈志賀重昂〉四)
3. ② たぐい。とも。なかま。
4. ③ 夫婦。つれあい。配偶。〔春秋左伝疏‐昭公二年〕
5. ④ ( ━する ) 修辞上、相対した二つの物事をならべて置くこと。対句(ついく)。
   1. [初出の実例]「名僧唱導必用_二対偶_一、以_レ法対_レ法、以_レ喩対_レ喩」(出典：円照上人行状（1302）)
   2. 「此邦の地名も詩中に用て雅馴なるも多く対偶(タイクウ)すべきもすくなからず」(出典：授業編（1783）九)
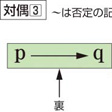
6. ⑤ 「ＡならＢ」というかたちの命題に対し、「ＢでなければＡではない」という命題。前者は、また後者の対偶となっている。命題とその対偶（命題）の正否は一致する。
   1. [初出の実例]「対偶法にて、其否定の標しを、肯定となせば、丁の対偶なる乙を得」(出典：致知啓蒙（1874）〈西周〉下)
7. ⑥ 機械の機構で、相接触する二つの機械要素を組み合わせたもの。軸と軸受け、ボルトとナットなど。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

対偶 (たいぐう)
contraposition

論理学の用語。伝統的論理学では，命題pに対してまず換質を次に換位を施して命題qが得られるとき，qをpの対偶と呼ぶ。例えば，p：〈すべてのSはPである〉の対偶は，q：〈いかなる非-PもSでない〉である。現代論理学では，A，Bを論理式とし，⊃は〈もし……ならば……〉，～は〈……でない〉を表す記号とするとき，式A⊃Bに対して，式～B⊃BAを対偶と呼び，〈A⊃Bと～B⊃～Aの真偽は一致する〉を対偶の法則law of contrapositionと呼ぶ。
執筆者：岡部 満

出典　株式会社平凡社「改訂新版　世界大百科事典」

普及版 字通

【対偶】たいぐう

相手。夫婦。また、修辞法の対句。〔甌北詩話、十二、七言律〕・魏以來、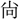ほ散行多く、對偶を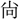(たつと)ばず。謝靈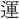の輩、始めて對屬を以て工と爲して自(よ)り、已に律詩の爲に端を開けり。

字通「対」の項目を見る。

出典　平凡社「普及版 字通」

日本大百科全書(ニッポニカ)

対偶（機械）
たいぐう
pair

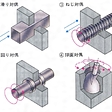
ボルトとナットのように、一定の相対運動をする機構のそれぞれの部分（機素）が接触し、互いに一定の拘束運動をするような組合せをいう。軸と軸受、一対の歯車などがその例である。対偶は、面接触をするものと、線または点接触するものとに分けることができる。面接触をする場合、その運動から次のようなものがある。〔1〕一方を固定すると他方は直線運動をする滑り対偶、〔2〕軸線の周りに回転運動だけをする回り対偶、〔3〕直線運動と同時に回転運動をするねじ対偶、〔4〕球面で接触し球の中心に対して球面運動をする球面対偶、などである。拘束が幾何学的に完全なものを拘束対偶、ばね、油圧、重力などの外力によって拘束しなければならないものを強制拘束対偶という。

［中山秀太郎］

対偶のおもな種類

対偶（数学）
たいぐう
contraposition

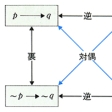
「pならばqである」という命題において、その仮設pと終結qとを交換して得られる命題「qならばpである」を元の命題の逆converseという。また、仮設と終結をそれぞれ否定して得られる命題「pでないならばqでない」を元の命題の裏inverse、そして、仮設と終結をともに否定したうえ両者を交換して得られる命題「qでないならばpでない」を元の命題の対偶という。一つの真である命題からつくった対偶はかならず真である。

［古藤　怜］

対偶

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

対偶
たいぐう
contraposition

形式論理学の用語。ある命題について，その帰結部分の否定を前提とし，前提部分の否定を帰結とした命題をもとの命題に対して対偶の関係にあるという。たとえば，「すべてのギリシア人が白いならば，ソクラテスは白い」を原命題とすれば，その対偶命題は「ソクラテスが白くないならば，すべてのギリシア人が白くあるのではない」となる。このように対偶関係にある2つの命題はトートロジーで，その真偽は常に相一致する。これを記号論理学の用語で記せば，(p⊃q) ≡ (～q⊃～p) となる。

対偶
たいぐう
pair

番 (つがい) ともいう。2つの機素 (機械を構成する個々の部品) が相接して相対的な運動をする場合，互いに対偶をなしているといい，面で接触しているときを面対偶，点または線で接触しているときをそれぞれ点対偶，線対偶と呼ぶ。ある一種の運動しかできないように拘束する場合を限定対偶といい，(1) 軸線方向にのみ運動する直進対偶，(2) 軸線のまわりに回転だけする回転対偶，(3) 回りながら一定の割合で軸方向に進むねじ対偶，の3種がある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の対偶の言及

【逆】より

…もとの命題が正しくても，逆は正しいとは限らない(x²＞4ならば，x＞2またはx＜－2が正しい命題)。また，もとの命題および逆のA,Bを，A,Bの否定におきかえたもの〈AでないならばBでない〉〈BでないならばAでない〉(前の例なら，〈実数xについて，x≦2ならばx²≦4〉および〈実数xについて，x²≦4ならばx≦2〉)を，それぞれもとの命題の裏obverse，対偶contrapositionという。もとの命題が正しければ対偶も正しく，対偶の対偶はもとの命題であるから，ある命題とその対偶とは同値であり，ある命題を証明するのに対偶を証明してもよい。…

【逆】より

…もとの命題が正しくても，逆は正しいとは限らない(x²＞4ならば，x＞2またはx＜－2が正しい命題)。また，もとの命題および逆のA,Bを，A,Bの否定におきかえたもの〈AでないならばBでない〉〈BでないならばAでない〉(前の例なら，〈実数xについて，x≦2ならばx²≦4〉および〈実数xについて，x²≦4ならばx≦2〉)を，それぞれもとの命題の裏obverse，対偶contrapositionという。もとの命題が正しければ対偶も正しく，対偶の対偶はもとの命題であるから，ある命題とその対偶とは同値であり，ある命題を証明するのに対偶を証明してもよい。…

【条件】より

…論理的条件の中心は現代論理の中核にある標準論理の条件で，いま任意の2命題をp,qとすると，p→qあるいはp⊃q等で表現され，その全体を条件(式)，→(または⊃)を条件詞(または条件記号)，pをqの前件，qをpの後件という。また，pをqの十分条件，qをpの必要条件というが，必要条件という命名の理由は，p,qのそれぞれを否定にして順をかえた〈qでないならばpでない〉は〈pならばq〉のいわゆる〈対偶〉で，両者は互いに等しく，したがって，〈pならばq〉とは〈qが成り立たなければpも成り立たない〉に等しい点にある。標準論理の条件は別名〈実質含意〉ともよばれ，標準論理の他の命題結合詞と同様に，p,qのそれぞれの真偽の値によって定義され，pが真，qが偽のときのみ全体が偽で，他の場合(pもqも真，pが偽でqが真か偽)にはすべて真とされる。…

【対句】より

…中国の詩文における修辞上の技法の一つ。中国語では一般に〈対偶〉という名称のほうが用いられる。並列された同字数の2句が，語法上からも，意味上からもシンメトリックに対応しあうように構成された表現形式をいう。…

※「対偶」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」