結晶構造（読み）ケッショウコウゾウ（英語表記）crystal structure

デジタル大辞泉

けっしょう‐こうぞう〔ケツシヤウコウザウ〕【結晶構造】

結晶内の原子・分子・イオンなどの配列状態。構造解析には、X線・電子線・中性子線などの回折が用いられる。

出典　小学館

精選版 日本国語大辞典

けっしょう‐こうぞうケッシャウコウザウ【結晶構造】

1. 〘 名詞 〙 結晶における原子、分子、イオンの配列状態をいう。代表的な型をもつ構造には、その物質名をつけて、岩塩型構造、ダイヤモンド型構造などと呼ぶ。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

結晶構造 (けっしょうこうぞう)
crystal structure

結晶中の原子の幾何学的な配列の様式を結晶構造という。分子も原子の集りによって幾何学的に構成され，分子構造をもつから，分子性結晶では，ある構造をもった分子が集まって，結晶構造という別の構造を幾何学的に構成していることになる。結晶の基本的な性質は，その結晶構造に依存している。したがって，結晶構造についての詳細な知識は結晶の物理的性質の研究に重要であるばかりでなく，必要とする物性をもった結晶を合成する指針ともなりうる。

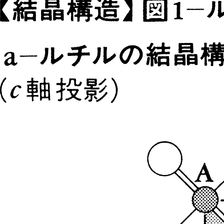
　結晶構造は一般に三次元的な周期性をもっているから，一つの単位胞の中の原子配列で構造全体を代表させることができる。一つの結晶について，その単位胞の定数，その中に含まれる化学単位の数（Z），空間群，単位胞の座標系に対する原子の位置座標などは，その結晶の結晶構造データ（あるいは結晶学的データ）といわれる。一例として，正方晶系に属しTiO₂の化学組成をもつルチルのおもな結晶構造データをあげると，単位胞の定数a＝4.593Å，c＝2.595Å，Z＝2，空間群P4/mnmで，原子座標x，y，zとしてはTiが0，0，1/2，Oが0.1945，0.1945，0である。これだけのデータから図1-aに示すようなルチルの構造図（c軸投影）をかくことができる。この構造をみると一つの単位胞の中に，4個の酸素原子と2個のチタン原子が存在するが，これら4個の酸素原子は空間群の対称操作で関係づけられており，互いに同価である。2個のチタン原子も同様に互いに同価である。したがって，この構造で対称的に独立な原子は1個のチタン原子と1個の酸素原子ということになる。この図の灰色で示した部分（c軸に沿っては，c軸の長さを1として0から1/2まで）は，空間群P4/mnmにおいて対称的に独立な部分で，このような部分をその空間群，あるいはその構造の非対称単位という。一般に，結晶の原子配列を記載するには，その結晶がもつ空間群の非対称単位の中に含まれる原子の座標だけで十分である。

構造単位の大きさ

結晶構造の幾何学的構成の単位をなす原子（あるいはイオン）は，原子核の周囲に電子が球状に分布している球と見なすことができる。しかし，その電子密度分布は，原子の中心から距離の指数関数的に減衰しているから，半径を物理的に定義づけるのは困難である。そのうえ，原子の電子密度分布は，それに隣接する他の原子の数，その他種々の物理的効果のため球対称から変形するから，あらゆる物質に通用する原子半径を一義的に決めることはできない。

　現在一般に用いられている原子半径あるいはイオン半径の概念は，主として結晶構造の解析によって得られた原子間距離の値に基づいている。結晶中で互いに近接する二つのO²⁻の距離は，数多くの物質について平均すると2.80Åであるので，O²⁻は半径1.40Åの球と考えることができる。この値を規準に用いると，結晶中での種々の陽イオンとO²⁻の距離を最もよく説明できるように陽イオンの半径を決めることができる。たとえばAl³⁺は0.535Å，Mg²⁺は0.720Å，Fe²⁺は0.780Å，Na⁺は1.02Åなどである。ただし，これらの値は陽イオンが6配位をとる場合であって，4配位の場合はそれぞれ約0.14Å小さくなる。そのよい例はSi⁴⁺で，4配位のとき0.26Åが，6配位をとると0.40Åとなる。O²⁻以外の陰イオンの半径はF⁻が1.33Å，Cl⁻が1.81Å，S²⁻が1.84Åで，いずれも陽イオンに比べて非常に大きい。例外はRb⁺（1.52Å），Cs⁺（1.67Å）などの4種類の陽イオンのみである。したがって，これらの陰イオンを含む結晶構造では，密に充てんした陰イオンの隙間に陽イオンが介在し，単位胞の計量的な性質は陰イオンの充てんの様式（最密充てん）で左右される傾向をもつ。図1-bは，aに太い矢印で示す酸素原子の層をa₁軸に沿って見たもので，各酸素原子は半径1.40Åの円でかかれている。この図からわかるように，この酸素原子の層はほぼ最密充てんに近く，c軸，a₂軸の長さはこのような酸素原子の配列で決まっている。円がわずかに重なっているのは，同じチタン原子に結合するO－O間の距離が2.80Åよりわずかに小さいためである。

　一般に陽イオンが中性の原子となると半径が約0.85Å大きくなり，また，陰イオンが中性原子となると約0.85Å小さくなる。したがって，一対の原子半径の和と，対応するイオン半径の和は一般に非常に類似した値をもつ。原子半径は，その和が共有結合の距離を与えるものであるが，それは金属結合の場合にもほぼ適用できる。

化合物の結晶構造

一つの化合物において最も電気陰性度の大きい原子を陰イオン，他の原子を陽イオンと呼ぶことにすると，化合物の結晶構造においては，陽イオンは陰イオンで取り囲まれているという共通の性質をもっている。したがって，各陽イオンについて，陰イオンの中心を頂点とする一つの多面体，すなわち配位多面体を考えることができる。この場合，陽イオンを囲む陰イオンの数（配位数）は陽イオンと陰イオンの半径の比と密接に関係している。このため，このような物質の結晶構造は多面体のつながりで表現することができる。ルチルの構造では各チタン原子が6個のOにより八面体的に配位されているから，この構造は図1-cに示すように八面体が各頂点あるいは稜を共有した三次元的骨格構造として表すことができる。図1-dにルチルの立体構造を示す。

　多面体が頂点を共有する場合には，次のようなポーリングPaulingの律則に従う。いま，陽イオンAの配位数をν，その電荷をqe（eは電気素量）とし，頂点を占める陰イオンをXとすると，一つのA－X結合の静電結合力の強さsはq/νで定義される。このとき，陰イオンの電荷を－Qeとすると，Q＝Σ（q_i/ν_i）が満足されなくてはならない。この式は，一つのXについて，それと結合する陽イオンとの間の静電結合力の総和をとることを意味している。多面体が正多面体でなく変形している際は，この関係は必ずしも満足されないが，それでも非常に高い近似で成立している。ルチルの例ではq＝4，ν＝6，またi＝3であるからQ＝4/6＋4/6＋4/6で，その総和は2となり，酸素原子の形式電荷と正確に一致していることがわかる。より複雑な構造の例としてカンラン石（Mg₂SiO₄）の構造を図2に示す。この場合でも上述の律則は正確に守られている。この図はカンラン石の構造を同価な二つの多面体層に分けて，その一つを示したもので，灰色で示す部分はMgを囲んで酸素原子が形成する八面体であり，四面体は［SiO₄］⁴⁻である。いま，Oに注目すると，この酸素原子は3個の八面体に共有され，さらに別の層の［SiO₄］⁴⁻とも共有されている。したがって，そのQは2/6×3＋4/4で，やはりQ＝2となる。

　このケイ酸塩のように，多種多様な化合物をつくりあげている炭酸塩，ホウ酸塩，リン酸塩などの酸素酸塩類の構造では，炭素，ホウ素，リンなどの原子が酸素原子で囲まれた陰イオンをつくりあげている（図3）。その配位数は一般に半径比で決まるが，このような陰イオンは共有結合の性格もそなえているので，結合の対称性により［AsS₃］³⁻のような形をとるものもある。これらの陰イオンにおいて静電結合力の強さsの値が1かまたは1に非常に近い値であるとき，互いに酸素原子を共有して，さらに大きな陰イオンをつくる傾向がある。図4に示すのはホウ酸塩（ホウ素原子が3配位のときs＝1，4配位のときs＝1.1），リン酸塩（s＝1.125），ケイ酸塩（s＝1）におけるそのような巨大陰イオンの中の簡単な例である。このような陰イオンと陽イオンが効果的に空間を充てんするようにして塩類の構造がつくられているのである。

　配位多面体が連なって構造をつくる際に，頂点でなしに稜あるいは面を共有すると構造の安定度は減少する。この効果は，原子価が大きく，配位数の小さな陽イオンほど大きい。したがって，ケイ酸塩ではSiO₄四面体は稜あるいは面を共有することがない。その理由は，そのような共有によって陽イオンどうしが著しく接近するからである。2価陽イオンを囲んで形成される八面体の場合は，八面体どうしの稜共有は図1-cの例のように一般的に存在する。しかしながら，面共有の八面体が存在する構造はほとんどない。アルミニウム原子を囲む酸素原子の八面体が面を共有しているコランダム（α-Al₂O₃）の構造は珍しい例外である。

　このように，二つの多面体が稜（あるいは面）を共有するときは，その多面体中の陽イオンは稜（面）に対して互いに逆方向に変位する傾向を示すが，陽イオンと陰イオン間の距離は一般に変化しない。それは共有されている稜（面）の長さ（面積）が縮むからである。ルチルの場合，共有稜の長さは2.53Åで，平均のO－O距離2.80Åよりかなり短い。このような短縮が起こるのは，陽イオン相互の反発が共有稜をつくっている陰イオン間の固有の反発力と平衡するまで働くためである。

構造型

物質，特に無機物質の結晶がすべてそれぞれ異なった形式の結晶構造をもつわけではない。いま，陽イオンをA，陰イオンをXとして，ルチルの化学式TiO₂を抽象的にAX₂で表現すると，この型の化学式をもつ多くの物質，すなわちSnO₂，VO₂，NbO₂，WO₂などの酸化物，またMnF₂，ZnF₂，FeF₂その他のフッ化物がルチルと同じ型の結晶構造をつくる。この構造の型はスズ石SnO₂で初めて発見されたのでSnO₂型といわれる。一つの構造型は，AX₂のような化学式の形，一つの空間群，および原子配列のトポロジーで定義される。ここで原子配列のトポロジーとは，図1-aのように結合している原子を線で結んだとき，その線の幾何学的な連なり方（あるいは多面体の連なり方）の特徴をいう。同じ構造型に属する物質は互いに同型（どうけい）といわれる。

　図2に示した構造も一つの重要な構造型であって，カンラン石構造型といわれる。この構造型では酸素原子は六方最密充てん型の配列をとっている。Mg₂SiO₄のMgをFe，Mn，あるいはNiなどで置き換えた物質も互いに同型である。このように，構造型を保存する陽イオンの入れ換えを同型置換という。このような場合，それらの物質の間には一般に固溶体が形成される傾向がある。

　構造型として最も基本的なものはAX型の化学式をもつ化合物の構造であって，NaCl型，CsCl型（図5-b）はその典型的な例である。前者ではCl⁻は立方最密充てん型の配列をとり，その八面体の空隙をNa⁺が占めている。このときNa⁺もまた立方最密充てん型の配列をなしている。これに対して，後者ではCs⁺はCl⁻がつくる立方体の中心，すなわち体心の位置に存在する。したがって，この場合Cs⁺は8配位となっている。

　原子が最密充てん型の配列をとる傾向を示すのはイオン性の結晶に限らない。典型的な共有結合でできているセン亜鉛鉱ZnSでも，S原子は立方最密充てん型の配列をとり（図5-c），その四面体空隙の半数をZnが占めてこの構造がつくられている。結合に方向性のある共有結合にもかかわらずこのような構造が可能なのは，Znの結合軌道の対称が四面体の対称と一致しているからである。この構造型でZnとSの区別をなくし，1種類の原子，たとえば炭素原子で置き換えると，ダイヤモンドの構造が導かれる（図5-d）。このような単体では，それが金属単体であるときは結合に方向性がないから，最密充てん型あるいはCsCl型の結晶構造をもつものが多い。また，金属結合によらない単体では図5-bのような構造型のほかに，結合軌道の幾何学的性格にしたがって，環状構造のように空間的に有限な構造，一次元的に無限な鎖構造，あるいは層状構造などをつくり，それらが単位となって結晶構造をつくりあげている。この際，各構造単位はなるべく効果的に空間を埋めるように配列している。

　構造の単位が密につまって結晶構造全体が構成されている傾向は有機結晶においても例外ではない。図6-aに示すのはオキシテトラサイクリン分子の立体構造モデルで，塩酸オキシテトラサイクリンC₂₂H₂₄N₂O₉・HClの結晶構造における一つの分子をそのc軸から見たものである。このような低対称の分子を一つの図形で表現して，分子が結晶の中で配列しているようすを示したのが図6-bである。c軸方向の相対的な高さを示すために，この図の中で分子は4種類の濃度で表現されている。このように分子が凝集した結果，a，b，c各方向に2回らせん軸が存在するような配列となっている。有機物質の多様性は一般にその構成単位である分子自身の多様性に依存しているから，有機結晶については構造型という概念はあまり意味がない。しかし，原子の凝集様式という観点からは，タンパク質のような有機の巨大分子の結晶と無機結晶の複雑な構造とは次のような共通点をもっている。タンパク質の結晶の場合は，アミノ酸残基が集まって高次構造をつくり，それが集まって巨大分子を構成し，それを単位として結晶構造がつくられている。これと同じように無機物質の複雑な結晶構造の多くのものは，ある構造型をもつ単位胞が集まって一つの構造単位をつくり，それが別の構造型をもつ単位胞の集りとともにさらに大きな構造をつくり，それが単位となって構造全体を構成しているのである。また，無機物，有機物を問わず，構造単位が密につまって結晶構造を構成する傾向があるのは，内部エネルギーが最小になるような配列をとる結果であって，図1-c，図2に示したような多面体は低いエネルギー状態の一つの表現にほかならない。

構造型の変化

アルカリ金属の塩化物でNaCl型構造をとるのは半径比が0.85より小さい場合で，その値をこすものはCsCl型に結晶する。一般に一つの構造型には，それに許容されるイオンの半径比あるいは分極性の強さに限度があり，それをこすと他の構造型に変わる。たとえ一つの構造型に許容される範囲の同型置換であっても，たとえば図4に示すケイ酸鎖状イオンを含む構造では，陽イオンの置換によりSi－O－Si角がわずかに変化し，鎖状構造が幾何学的に微妙な変化を示す。それは，このような酸素酸塩では陰イオン基が陽イオンの配位多面体と連結しているため，陰イオン基の形は陽イオン多面体の大きさおよびその連なり方によって制御されているためである。

　ある構造型の1種類の陽イオンAが，2種類以上の陽イオン，たとえばB，Cで置換される際，その置換が統計的に完全に無秩序であれば構造型は必ずしも変化しないが，BとCが一定の秩序でAを置換すると，必然的に格子周期が変わり，もとの構造に比べてより大きな単位胞の構造となる。この新しい構造をもとの構造の超構造という。鉱物，合金などの構造に超構造がしばしば出現する。

　置換ではなしに物理的環境の変化に伴う構造変化（相変化）の際も，配位数の変化に一つの定まった傾向が見られる。たとえば，CsClは約450℃でNaCl型に変化し，Csの配位は8から6へ減少する。一般に温度依存の構造変化では，温度の上昇とともに陽イオンの配位数がより少ない構造へ変化する。これは，熱振動の自由度が増大する方向へ変化するからである。逆に，圧力に対しては，体積の減少に伴ってより密な構造となるため，配位数は増大する方向へ変化する。たとえば，水晶（SiO₂）は常温，常圧では図7に示すようにSiO₄四面体が頂点を共有してつくる右らせん，あるいは左らせん構造を単位とする骨格構造をもち，右水晶と左水晶の対掌体が存在するが，1000℃，10万気圧ではSnO₂型（図1）に変化し，左右の区別は消失して，Siは6配位となる。このとき，比重は2.65から4.35と増大する。このような物質は地球上でも発見されているが，それは隕石の衝突により衝撃的に発生した温度，圧力によるものである。圧力相変化の他の例として興味あるのは図2のカンラン石である。この物質は約1000℃，20万気圧でMgおよびSiそれぞれの相対的配列がより密なスピネル型構造に変化し，このとき体積が約10%減少する。このカンラン石は地球内部の主要な構成物質であるので，それで構成されている岩体がなんらかの運動によって上記の物理条件をもつ地球深部（約400km）まで運ばれると，スピネルへの相変化を起こし，そのとき急激に体積が減少することになる。深発地震の原因は一つの可能性としてこのようなカンラン石→スピネルの相変化により誘発されるのではないかと想像されている。このように，幾何学模様で表される結晶構造の研究は，われわれを脅やかす自然の巨大エネルギーとも関連をもっている。図6に示したような生化学的に重要な物質あるいはタンパク質の構造研究は生命科学に，またもろもろの無機，有機物質の結晶構造の研究はわれわれの日常生活の向上に密接な関係をもっている。
→結晶
執筆者：竹内 慶夫

図1～図7

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

結晶構造
けっしょうこうぞう
crystal structure

結晶格子での原子の配列。結晶構造の決定には、単結晶X線回折法のほか、中性子線回折法、電子線回折法、粉末X線回折法なども利用され、核磁気共鳴吸収法、赤外・ラマン分光法、メスバウアー分光法、核四重極共鳴吸収法なども補助的に利用されることがある。結晶構造は、その結晶の属する晶系、晶族（点群）、あるいは単位胞の空間群、格子定数ならびに単位胞内の原子座標によって基本的に示される。現実の結晶では、各原子は熱振動しているので、その程度を示す温度因子も原子座標とともに示されることが多い。

　測定および解析技術の進歩によって、結晶構造解析に関する報告例は爆発的に増加しつつあるが、それでも、現在知られている結晶性物質の種類の数に比べれば、微々たるものである。複雑な有機化合物、錯体、タンパク質などの結晶構造を系統的に分類するには、まだ十分な数の報告例が蓄積されているとはいえない状況にある。

［岩本振武　2015年8月19日］

無機化合物の結晶構造の分類

単位胞が比較的小さく、組成も複雑ではない無機化合物については、多くの典型的結晶構造が知られており、その典型例となる化合物あるいは鉱物の名を冠した構造の型が分類されている。

［岩本振武　2015年8月19日］

組成AX（Aは陽性元素、Xは陰性元素）となる二元化合物の構造

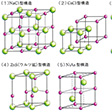
塩化ナトリウム（岩塩）型、塩化セシウム型、閃(せん)亜鉛鉱型、ウルツ鉱（繊維亜鉛鉱）型、ヒ化ニッケル型、酸化パラジウム型などがある。それらにおける構造の差異は、イオン半径比や結合に及ぼす共有性の効果の程度の差によって生ずると考えられる。

　塩化ナトリウム型（図Aの(1)）と塩化セシウム型（図Aの(2)）は、同じアルカリ金属に属する陽イオンの塩化物ではあるが、セシウムイオンのイオン半径がナトリウムイオンより大きいため、同じ構造にはならない。塩化ナトリウム型では、塩化物イオンのつくる面心立方格子の中に生ずる八面体型6配位の位置にナトリウムイオンが収まるが、セシウムイオンは大きすぎて、この位置には収まらない。セシウムイオンでは配位数が8に増大し、塩化物イオンのつくる単純立方格子の中に生ずる立方体型8配位の位置に収まる。

　閃亜鉛鉱（図Aの(3)）もウルツ鉱（図Aの(4)）もともに硫化亜鉛ZnSを主成分とする鉱物であるが、前者では硫化物イオンが面心立方格子、後者では六方格子をつくり、それぞれの四面体型4配位の位置に亜鉛イオンが収まる。亜鉛イオンと硫化物イオンとの半径比は、ハロゲン化アルカリに比べれば小さくなっている。硫化亜鉛の場合、閃亜鉛鉱型が室温安定形で、ウルツ鉱型が高温安定形である。また、陽イオンによる陰イオンの分極の程度も大きくなり、共有結合性の寄与も大きいと考えられている。

　ヒ化ニッケル型（図Aの(5)）では、陰性のヒ素原子が六方格子をつくり、その八面体型6配位の位置に陽性原子のニッケルが収まる。ニッケル原子間の距離2.51Åは、金属結晶での距離の2倍であるが、結晶としての性質は共有結合性ないし金属結合性を帯びている。

　酸化パラジウム型（PdO）では、結合の方向性が著しくなり、共有（配位）結合の寄与も大きい。正方晶系の単位胞中でパラジウムイオンは4個の酸化物イオンに正方平面体型4配位構造で囲まれるが、逆に、酸化物イオンは4個のパラジウムイオンによって正四面体型4配位構造で囲まれる。

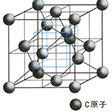
　共有結合性の強い二元化合物では、ダイヤモンド型（図B）構造と類似した閃亜鉛鉱型構造のもののほか、黒鉛に似た層状構造を示すものがあり、窒化ホウ素BNがその例となる。

［岩本振武　2015年8月19日］

AX₂型化合物の構造

蛍石型（CaF₂）、ルチル型（TiO₂）、クリストバル石型（SiO₂）、ヨウ化カドミウム型（CdI₂）、塩化鉛(Ⅱ)型（PbCl₂）などがある。

　蛍石型（図Cの(1)）では、カルシウムイオンが面心立方格子をつくり、そのすべての四面体型4配位位置にフッ化物イオンが位置する。逆に、カルシウムイオンは、フッ化物イオンのつくる単純立方構造の中心に収まることになる。ルチル型は4₂螺旋(らせん)軸をもつ正方晶系に属するが、チタンイオンは6個の酸化物イオンによって八面体型配位を受け、1個の酸化物イオンは3個のチタンイオンに配位している。クリストバル石型（図Cの(2)）ではケイ素原子がダイヤモンド型構造の炭素原子と同じ位置を占め、各ケイ素原子を四面体的に結ぶ線上の中点に酸素原子が位置し、共有結合による三次元構造が形成される。

　ヨウ化カドミウム型構造（図Cの(3)）では、ヨウ化物イオンがほぼ六方最密構造に近い配置をとり、層間の八面体型6配位位置にカドミウムイオンが収まるが、その収まり方は1層置きとなり、陰陽陰―陰陽陰―の各イオン層の積層構造になる。そのため、陰イオンどうしの接する層間での劈開(へきかい)がおこりやすく、カドミウムイオンとヨウ化物イオンの間の結合も共有性が強くなる。

　塩化鉛(Ⅱ)型では、鉛イオンは塩化物イオン9個によって正方面冠三方柱形に配位され、Pb-Cl原子間距離は共有結合性を示すとともに、著しく不均化する。これらのように、一見イオン結晶的に考えられる組成の無機化合物でも、構成原子の組合せによってさまざまな構造が現れる。

［岩本振武　2015年8月19日］

その他の結晶構造型

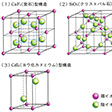
酸化物に限定して例示すると、AO₃型酸化物の酸化レニウム(Ⅵ)ReO₃では、Oを頂点とする正八面体型のReO₆単位が互いに頂点を共有して単純立方格子をつくる三次元構造をとる（図Dの(1)）。酸化タングステン(Ⅵ)WO₃ではこの構造にひずみを生じて単斜晶系となる。タングステンと同族のモリブデンの酸化物MO₃では、ひずんだMoO₆八面体単位が稜(りょう)あるいは頂点を共有する二次元の層構造をとり、結晶は積層構造の斜方（直方）晶系となる。

　ABO₃型酸化物の一例に灰チタン石(かいちたんせき)（ペロブスカイト）型構造（図Dの(2)）がある。灰チタン石は主成分CaTiO₃の複酸化物鉱物であるが、イオン半径が大きいA陽イオン（この場合はカルシウム）が単純立方格子をつくり、その面心の位置に酸化物イオンが入り、立方体の中心にイオン半径の小さいB陽イオン（チタン）が収まる。理想構造では立方晶系になるが、実際の化合物では正方晶系、三方晶系、あるいは斜方（直方）晶系にひずむものが多い。灰チタン石ではAは2価、Bは4価の陽イオンであるが、Aが1価、Bが5価の陽イオンとなる組合せでもこの構造をとる例が知られている。

　AB₂O₄型酸化物の代表的な一例であるスピネルは主成分MgAl₂O₄の鉱物で、立方晶系に属している（図Dの(3)）。単位胞は、酸化物イオンの面心立方格子がa、b、c3軸方向にそれぞれ2単位連結した、計8個分に相当する体積をもち、その中に8式量単位分が入る。原点は酸化物イオンによる正四面体型4配位の位置に置かれ、原点と等価な8個の位置にマグネシウムイオンが入る。アルミニウムイオンは正八面体型6配位の位置になる(1/4, 1/4, 1/8)とその等価点16個に入る。2価のAイオン、3価のBイオンの組合せによってこの種の構造をとる例は多いが、スピネルのAの位置にBの半分（8個）が入り、Bの位置に残りのBとAが入る逆スピネル型構造や、A、Bが無秩序に入る乱れスピネル型構造をとるものもある。一般にフェライトとよばれるものはM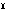Fe₂O₄型の複酸化物であり、鉄(Ⅲ)イオンの半分がスピネルのAの位置に入った逆スピネル構造をとると強磁性になる。

　特殊な結晶構造をとるものの例に包接化合物がある。包接化合物は、ホストとよばれる主体構造が籠(かご)状、トンネル状などの空間をつくり、ゲストとよばれる比較的小さい分子がその空間の中に収まって生成する化合物であるが、ホストとゲストとの間に強い化学結合はなく、空間と分子の間で寸法と形が適合する場合にだけ生成する。

［岩本振武　2015年8月19日］

『桐山良一著『無機化学構造』（1978・岩波書店）』

[参照項目] | ウルツ鉱型構造 | X線回折 | 塩化カドミウム型構造 | 塩化セシウム型構造 | 塩化ナトリウム型構造 | 塩化鉛（Ⅱ）型構造 | 結晶 | スピネル型構造 | 閃亜鉛鉱型構造 | 包接化合物 | 蛍石型構造 | ヨウ化カドミウム型構造 | ルチル型構造

典型的な結晶構造の例（AX型化合物）〔…

典型的な結晶構造の例（ダイヤモンド型構…

典型的な結晶構造の例（AX型化合物）〔…

典型的な結晶構造の例（その他の結晶構造…

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

結晶構造【けっしょうこうぞう】

結晶の内部における原子の規則正しい配列様式。配列の単位は結晶格子の格子点に位置する原子，原子団，分子，イオンなどで，それらが各種の化学結合により結合（たとえば塩類の結晶におけるイオン間のイオン結合）し，その結合の種類により結晶の物理的性質が支配される。結晶構造の解析は，実験的には主としてＸ線回折により行われ，理論的には空間群の理論により決定される。代表的な結晶構造のタイプは岩塩型とかダイヤモンド型というふうに物質名を冠して呼ばれる。
→関連項目オングストローム｜結晶学｜結晶形

出典　株式会社平凡社

化学辞典 第2版

結晶構造
ケッショウコウゾウ
structure of crystal

結晶の構成要素(原子，イオン，あるいは分子)の配列の仕方，とくに分子の構造およびそれらの三次元的配列をいう．それらは周期的に配列した格子構造をとる．その単位の格子のなかの原子やイオンや分子は，なんらかの対称操作で関係づけられている．対称要素を三次元の周期構造を満足するように組み合わせる方法は230通りあり，これを空間群という．したがって，結晶構造は単位格子の大きさ，空間群の種類，対称操作に対して独立な原子の種類，数，座標で記述することができる．これらの値を求めることを結晶構造解析という．いままで知られた結晶構造のなかで，比較的簡単で典型的な構造には，たとえばダイヤモンド型構造や岩塩型構造というように，その型の構造をとる結晶のうちで，代表的な物質名をとった名前がつけられている．現在では，タンパク質のような複雑な分子に至るまで多数の結晶構造が明らかにされている．結晶の物理的，化学的性質の理解のためには，結晶構造の知識が基本となる．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

結晶構造
けっしょうこうぞう
structure of crystal

原子あるいは分子が規則的に配列した固体を結晶といい，原子または分子の三次元空間における配列の仕方を結晶構造という。結晶構造は，三次元空間における3つの座標軸に沿った単位長さから成る構造の平行移動の組合せで表すことができる。各座標軸間の角度が 90度かそうでないか，各軸に沿う単位長さが等しいか等しくないかによって，立方晶系，正方晶系，六方晶系など7つに分類できる。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の結晶構造の言及

【結晶】より

…これは結晶の微視的状態とよばれるものである。例えば図7のaは大円で表した原子と，その向かって左下側にある小円の原子との1組で構成単位を形成して，この単位が前後･左右･上下にそれぞれの方向ごとに定まったある間隔で繰り返して互いに平行に並んでいる結晶構造を示す。
［結晶格子］
　これらの単位は図7のaに便宜的に描いた破線の枠に従って配列しているとみることができるので，bのようにこの枠(これを空間格子，結晶格子あるいは単に格子という)を取り出して，それが限りない広がりをもつと理想化して考えることにする。…

※「結晶構造」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」