ベクトル空間（読み）ベクトルクウカン（英語表記）vector space

デジタル大辞泉

ベクトル‐くうかん【ベクトル空間】

集合Vの任意の二つの元x、yに対して和x＋yが定義され、任意の元xと任意の実数αに対して積αxが定義され、この和と積に関して交換・結合・分配の法則などが成立するとき、この集合Vをベクトル空間という。線形空間。

出典　小学館

精選版 日本国語大辞典

ベクトル‐くうかん【ベクトル空間】

1. 〘 名詞 〙 直面する状況の下で、ベクトルと考えられるもの全体の集合のこと。線形空間。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

ベクトル空間
べくとるくうかん
vector space

線形空間ともいう。平面ベクトルと同じ計算法則を満たす加法と実数倍の定められた空間をいう。ここにいう計算法則とは、平面ベクトルや空間ベクトルに対して成立する以下の法則のことである。いまa、b、cを任意のベクトル、k、lを任意の実数とするとき、（1）(a+b)+c=a+(b+c)（2）a+0=0+a=a（3）a+(-a)=(-a)+a=0（4）a+b=b+a（5）k(a+b)=ka+kb（6）(kl)a=k(la)（7）(k+l)a=ka+la（8）1a=aしたがって厳密には、ある集合に加法と実数倍が定義されていて、これについて法則（1）～（8）が成り立つときに、この集合をベクトル空間ということになる。またこのとき集合の元をベクトルという。

　平面ベクトル、空間ベクトルの全体などは、もちろん、いま定義した意味でのベクトル空間であるが、他の例としては、〔1〕n項数ベクトルの全体、〔2〕一つの集合上の実数値関数の全体、とくに数列の全体、〔3〕解析学に現れるさまざまな関数空間、連続関数全体、微分可能な関数の全体、解析関数の全体、〔4〕不定元Xについての多項式全体などがある。

［高木亮一］

線形写像

二つのベクトル空間の間の写像fは、加法および実数倍と可換なとき、つまり
　　f(ka+lb)=kf(a)+lf(b)
を満たすとき、線形写像といわれる。とくに、fの値域が実数であるときは、線形形式といわれる。平面ベクトルや空間ベクトルの正射影は線形写像である。導関数をとることは、微分可能関数から実数値関数への線形写像をとることである。定積分を行うことは、連続関数からの線形形式である。

［高木亮一］

同形と次元

二つのベクトル空間は、線形写像による1対1対応がつくとき、同形であるという。n項数ベクトル空間と同形なベクトル空間は、有限次元であるといい、その次元をnと定める。このとき、n項数ベクトル空間の基本ベクトルe₁、e₂、……、e_nに対応するベクトルa₁、a₂、……、a_nが存在して、任意のベクトルはそれらの線形結合、すなわちk₁a₁+k₂a₂+……+k_na_nの形にただ一通りに表される。このようなベクトルa₁、a₂、……、a_nの組みを、ベクトル空間の一つの基という。

［高木亮一］

行列と線形写像

m次元ベクトル空間Vからn次元ベクトル空間Wへの線形写像fをとる。また、V、Wにそれぞれ基a₁、a₂、……、a_m、およびb₁、b₂、……、b_nを定めておく。

f(a_i)=F_i1b₁+F_i2b₂+……+F_inb_n
　　　(i=1,2,……,m)
であるとき、Vの任意の元k₁a₁+……+k_ma_mのfによる値は、
　f(k₁a₁+……+k_ma_m)
　=k₁f(a₁)+……+k_mf(a_m)
　=(k₁F₁₁+……+k_mF_m1)b₁
　+(k₁F₁₂+……+k_mF_m2)b₂
　+……+(k₁F_1n+……+k_mF_mn)b_n
となって、基の各ベクトルの値f(ai)によって完全に決まる。このときfにn行m列の行列(F_ij)を対応させる。逆に、任意のn行m列の行列(G_ij)が与えられると、
　g(a_i)=G_i1b₁+……+G_inb_n
　(i=1,2,……,m)
により基の各元の値を決めて、線形写像が定まる。このように二つの有限次元ベクトル空間の間の線形写像は、それぞれに基を定めることにより、行列と一対一に対応している。とくに、一つの有限次元ベクトル空間から自分自身への線形写像は正方行列に対応する。

［高木亮一］

双対空間

ベクトル空間が与えられると、そこから出発して、新しいベクトル空間を構成する方法が多数ある。ここでは、双対(そうつい)なベクトル空間といわれるものをつくってみよう。Vの線形形式全体をV^*と置く。V^*の任意の二元、ψと、任意のスカラーkに対して、Vからの二つの実数値関数、+ψ,kを
　　(+ψ)(a)=(a)+ψ(a)
　　(k)(a)=k((a))
と定める。ここに、aはVの任意の元である。このとき、+ψ,kはともにV^*の元になるからV^*に加法と実数倍が定義されたわけである。これについて、法則（1）～（8）が成り立つから、V^*はベクトル空間となる。このV^*をVの双対空間という。Vの元を反変ベクトル、V^*の元を共変ベクトルという。

［高木亮一］

計量ベクトル空間

内積、つまり平面ベクトルでいう内積と同じ計算法則を満たす二つのベクトルから実数への関数が与えられているベクトル空間を、計量ベクトル空間という。計量ベクトル空間では、ベクトルの長さや、二つのベクトルの間の角度を測ることができる。計量ベクトル空間の基a₁、……、a_nは、各a_iの長さが1で、互いに直交するとき正規直交系であるという。このとき二つのベクトルx₁a₁+……+x_na_n,y₁a₁+……+y_na_nの内積は、x₁y₁+……+x_ny_nと計算される。計量ベクトル空間にはかならず、正規直交系がとれる。

［高木亮一］

[参照項目] | テンソル

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ベクトル空間 (ベクトルくうかん)
vector space

空間のベクトルにはスカラー倍，平行四辺形の法則による和が定まる。ベクトル全体とこのスカラー倍，和をいっしょに考えたものをベクトル空間という。ベクトルのスカラー倍，和は次の性質をもつ。（1）a＋b＝b＋a，（2）（a＋b）＋c＝a＋（b＋c），（3）零ベクトル0についてa＋0＝a，（4）かってなベクトルaについてa＋a′＝0となるa′が存在する，（5）スカラーα，βについて，（α＋β）a＝αa＋βa，（6）スカラーα，ベクトルa，bについて，α（a＋b）＝αa＋αb，（7）スカラーα，βについて，（αβ）a＝α（βa），（8）1a＝a。（4）のa′は各aについて一意的に定まり，（－1）aと同じものである。これを－aと書く。

　一般に集合Vにスカラー倍，和が定まって，上記（1）～（8）を満たすとき，Vはベクトル空間であるといい，Vの元をベクトルと呼ぶ。ベクトル空間Vの任意の二元a，bについて，実数（a，b）が定まり，（a＋b，c）＝（a，c）＋（b，c），（a，b）＝（b，a），（αa，b）＝α（a，b），さらに（a，a）＝0ならば，a＝0であるという性質をもつとき，（a，b）をaとbの内積という。この内積に関するベクトルaの長さ｜a｜は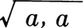と定める。（a，b）＝0のとき，aとbは直交するという。Vに有限個の元a₁，……，a_nが存在して，Vの各元がα₁a₁＋……＋α_na_nという形に書けるとき，Vの元e₁，……，e_rで，｜e_i｜＝1，（e_i，e_j）＝0（i≠j），Vの各元はβ₁e₁＋……＋β_re_rという形に書けるというものがある。これをVの正規直交基という。これを座標ベクトルと考えれば，Vはユークリッド空間の有向線分のベクトル空間と同じものと考えられる。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

ベクトル空間【ベクトルくうかん】

線形空間とも。一つの集合Vがあり，Vの任意の二つの元x，yに対しその和と呼ばれる第三の元x＋yを定める規則と，Vの任意の元xと任意の実数aに対しxのa倍と呼ばれるVの元axを定める規則が与えられており，次の1.〜8.の条件をみたしているとき，Vをベクトル空間といい，Vの元をベクトルという。1.x＋y＝y＋x，2.x＋（y＋z）＝（x＋y）＋z，3.任意のxに対しx＋０＝xとなるVの元０が存在する，4.xに対しx＋（−x）＝０となるVの元−xが存在する，5.a（x＋y）＝ax＋ay，6.（a＋b）x＝ax＋bx，7.（ab）x＝a（bx），8.1x＝x。ここでx，y，zはVの任意の元，a，bは任意の実数。axの形の元をxのスカラー倍といい，実数aをスカラーという。スカラーとしては実数のかわりに複素数をとってもよい。そのときはVを複素ベクトル空間ともいう。またさらに一般に任意の体Kの元をスカラーとしてもよい。このときVをK上のベクトル空間という。たとえばnを任意の自然数とするとき，n個の実数を順序をつけて並べたx＝（x₁，…，x(/n)）の全体はベクトル空間を作る。
→関連項目アフィン空間｜空間（数学）｜次元（数学）｜スカラー｜線形写像｜ヒルベルト空間

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

ベクトル空間
ベクトルくうかん
vector space

K を任意の体とする。集合 V の任意の2つの元 (ベクトル) a，b に対して加法 a＋b∈V が，K の任意の元αと V の任意の元 a に対して，乗法 α・a∈V が定義されていて，次の条件が成り立つとき，V を K の上のベクトル空間という。
(1) a＋b＝b＋a
(2) (a＋b)＋c＝a＋(b＋c)
(3) 任意の a，b∈V に対して a＋x＝b である元 x∈V がただ1つ存在する。
(4) 1・a＝a
(5) α(βa)＝(αβ)a
(6) α(a＋b)＝αa＋αb
(7) (α＋β)a＝αa＋βa。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のベクトル空間の言及

【線形空間】より

…これらを一般化して，次のように線形空間を定義する。集合Vと体Kが与えられて，次の条件(9)～(10)を満たすとき，VはK上の線形空間またはベクトル空間vector spaceであるといい，Vの元をベクトル，Kの元をスカラーと呼ぶ。(9)Vのかってな2元a，bについてその和a＋bが定まり，Kの任意の元αとVの任意の元aについてVの元αa(aのスカラー倍)がきまる，(10)この和について，Vはアーベル群になり，スカラー倍について，上記(5)～(8)が成立する。…

【線形空間】より

…これらを一般化して，次のように線形空間を定義する。集合Vと体Kが与えられて，次の条件(9)～(10)を満たすとき，VはK上の線形空間またはベクトル空間vector spaceであるといい，Vの元をベクトル，Kの元をスカラーと呼ぶ。(9)Vのかってな2元a，bについてその和a＋bが定まり，Kの任意の元αとVの任意の元aについてVの元αa(aのスカラー倍)がきまる，(10)この和について，Vはアーベル群になり，スカラー倍について，上記(5)～(8)が成立する。…

※「ベクトル空間」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」