自励振動（読み）ジレイシンドウ（英語表記）self-excited oscillation

デジタル大辞泉

じれい‐しんどう【自励振動】

振動体それ自体の運動によって、振動的ではない外力からエネルギーを取り込むことで起こる振動。振幅は増大または減衰せずに持続する。擦弦楽器の弦や木管楽器のリードの振動、航空機のフラッターなどに見られる。

出典　小学館

改訂新版　世界大百科事典

自励振動 (じれいしんどう)
self-excited oscillation

外部から振動的入力を与えられることなしに持続する振動を自励振動と呼び，自励振動を生ずる系を自励振動系と呼ぶ。われわれが日常接する機械的，電気的，また化学的な周期現象の多くが自励振動に起因していると考えられる。自励振動の最も典型的なものは，はじめ真空管発振器の特性を調べるために導かれた次のファン・デル・ポールVan der Pol方程式で表されるものである。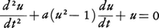

ここでa＞0，tは時間を表し，uはtの関数である。

　この方程式で記述される系の状態は，変数u（t）とその時間変化du（t）/dtの組（u（t），du（t）/dt）の値によって表すことができる。この組の全体を相平面という。ある初期状態から出発した系の状態の時間的経過に対応して相平面内に一つの軌道がえがかれる。上式の振動系の相平面には一つの閉軌道があって，相平面の原点（0，0）以外の点を初期状態とする系の軌道は時間の経過とともにこの閉軌道に近づく（図）。このような閉軌道は安定なリミットサイクルと呼ばれ，周期的な自励振動に対応している。この振舞いはごく概略的には，系へのエネルギーの入出量によって次のように説明することができる。すなわち，上式においてdu/dtの係数は系へのエネルギーの入出量に対応するものであり，この値が負のとき系へエネルギーが入り，正のとき系からエネルギーが出ることを表す。上式の場合にはこの係数がuの値によって変化し，u²＜1では負の値をとるので，u²が小さい所ではエネルギーが入ることになり振動は増大する。一方，u²＞1では正となるので，u²が大きい所では振動は減衰する。したがって，この中間に安定なリミットサイクルが存在することになる。

　このような負の係数をつくるものは一般に負性抵抗と呼ばれる。自励振動が発生するためには上の例のように負性抵抗的要素によってエネルギーが系に入ることが必要であるが，機械系では摩擦抵抗など，電気系では半導体素子など，また化学系では自己触媒型反応などによって実現されている場合が多い。上式でaを無限に大きくした極限は弛張振動と呼ばれる間欠的振動に対応し，温度調節器，間欠泉，さらに生物のペースメーカー細胞などの振動はこれに近い。逆にaを0に近づけたものはリミットサイクルが円に近づき，その振動は正弦波振動となる。

　多くの自励振動系は，上に見たように1個あるいは数個の単純なリミットサイクルをもつことが多いが，温度こう配のある流体の状態を特徴づけるローレンツLorenz方程式と呼ばれる3階の方程式などの場合にはきわめて複雑な軌道をもち，カオス的な振動を生ずるものもある。
執筆者：吉沢 修治

図－自励振動

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

自励振動
じれいしんどう
self-excited oscillation

周期的でない外力が加えられた系に励起され，成長し，持続する振動。たとえば，バイオリンなどの弦を弓で押しつけて一定の方向へ一定の速さで引き，摩擦によって誘起させる弦の振動がある。管楽器のリード，風による電線の鳴きなども空気が狭いところを通るときの摩擦が起す自励振動である。機械，タービン，自動車，航空機などの異常振動もこれに起因することが多い。自励振動は，負の抵抗が働くときに振幅が増大する振動を生じる現象であり，正の抵抗が働いて振幅が減少する減衰振動の逆振動である。電気振動回路の発振，自動制御系の時間遅れ振動などは，負抵抗の非線形項が発振に重要な役割を果し，その研究は非線形振動論の発展の契機となった。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の自励振動の言及

【振動】より

…例えばバイオリンの弦は弓で一方向にこすることによって振動を起こす。このような現象を自励振動という。電気振動における自励振動は発振回路に利用されている。…

※「自励振動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」