精選版 日本国語大辞典 「アンペールの法則」の意味・読み・例文・類語
日本大百科全書(ニッポニカ) 「アンペールの法則」の意味・わかりやすい解説
アンペールの法則
あんぺーるのほうそく
電線に電流が流れると、電流の周りに磁界(磁場)が生ずる。この電流と磁界との間に成り立つ次の関係をアンペールの法則という。「磁界の中に閉曲線をとり、この閉曲線上で磁界Hの閉曲線の接線方向の成分を積算する。この値は閉曲線を貫いて流れる全電流に等しい」。これはフランスの物理学者アンペールが発見した(1822)。電流から発生する磁界を表す基本法則であるビオ‐サバールの法則と同等の法則である。
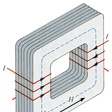
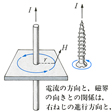
は十分に長い直線電流の場合である。このとき、磁力線は電流を中心とする同心円となる。半径rの円をとって、その上の磁界をHとする。この磁力線を閉曲線にとると、この閉曲線上の磁界Hの接線成分の積算量は2πrHである。アンペールの法則によれば、この値は、この閉曲線を貫く電流Iに等しい。はアンペールの法則の鉄芯(しん)のあるコイルへの応用例を示す。鉄芯の中の磁力線の1周の長さをL、磁界の平均的な強さをHとすれば、この磁力線上の磁界の接線成分の積算量はLHである。この閉曲線を貫いて流れる電流は、コイルがN回巻きとすればNIである。アンペールの法則によればLH=NIとなる。電界が時間的に変化するとき、その空間には電束電流が流れる。アンペールの法則における全電流には、一般には通常の電流のほかに電束電流も含める。このように考えると、コンデンサーを含む電流回路、とくにコンデンサーの電極間の空間の磁界に対してもアンペールの法則を例外なく適用できるようになる。
なお、電流がつくる磁界の方向を表す右ねじの法則も、アンペールの法則ということがある。
[山口重雄]
改訂新版 世界大百科事典 「アンペールの法則」の意味・わかりやすい解説
アンペールの法則 (アンペールのほうそく)
Ampère's law
フランスの物理学者A.M.アンペールが発見した定常電流のまわりに生ずる磁場に関する法則。図1に示すように定常電流i(A)のまわりには,電流iの向きに右ねじを進めるようなねじの回転方向に沿って磁場Hが生ずる。いまかりに単位磁極があって,これを電流iをとり囲む一周回路について一周させるときに,単位磁極のする仕事はiに等しいことをこの法則は示している。アンペールの法則を用いると,対称性のよい磁場分布の場合には簡単に磁場の値を計算することができる。例えば無限に長い直線電流から,それに垂直にr(m)の点Pの磁場H(A/m)を求めるには,点Pを通り直線電流を中心軸とする半径r(m)の円周に沿って単位磁極を運ぶときに,単位磁極のする仕事を考えればよい。単位磁極にはHの力が作用し,この力は円周上で一定だから,単位磁極のする仕事はこの力に円周の長さ2πrを掛ければよい。すなわち,アンペールの法則により,2πrH=iとなるからH=i/2πrと求まる。また,無限に長いソレノイドの内部には,その長さの方向に一様な磁場Hが生ずるが,その外側の磁場は0であることがわかっている。単位長さ当りの巻数がn(m⁻1)のソレノイドにi(A)の電流を流す場合に内部の磁場H(A/m)を求めるには,図2に点線で示すような一周回路に沿って,アンペールの法則を用いるとH=niと求めることができる。
執筆者:近角 聡信
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「アンペールの法則」の意味・わかりやすい解説
アンペールの法則【アンペールのほうそく】
→関連項目ビオ=サバールの法則
出典 株式会社平凡社百科事典マイペディアについて 情報
法則の辞典 「アンペールの法則」の解説
アンペールの法則【Ampere's law】
なお,電流 I を取り巻く任意の閉曲線上における磁界の強さ H は
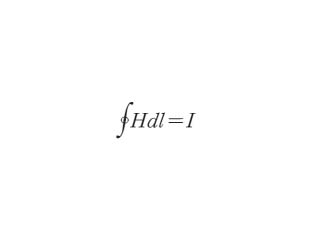
で表される.ここで積分
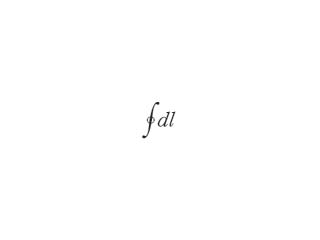
は閉曲線に沿って一回りするぶんの線積分を示す.この後半分は通常ビオ‐サヴァールの法則*というが,右ネジの法則と一緒にして「アンペールの法則」ということもしばしばある.
ブリタニカ国際大百科事典 小項目事典 「アンペールの法則」の意味・わかりやすい解説
アンペールの法則
アンペールのほうそく
Ampère's law
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内のアンペールの法則の言及
【電磁誘導】より
…式で表すと, rotH=∂D/∂t ……(2)となり,これは(1)式と対称的な式となっている。この式は,電流iがその周囲に磁場を作る現象,すなわちアンペールの法則, rotH=i……(3) に類似しているので,∂D/∂tを変位電流と呼び,(2)(3)を合わせた式, rotH=i+∂D/∂tを拡張されたアンペールの法則ということがある。当時(2)の式を直接実証する実験はなかったが,電流以外にも磁場を作る原因があると考えたことは,マクスウェルの天才的な着想であった。…
※「アンペールの法則」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...