出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
イデアル
Ideal[ドイツ]
整数は素数の積にただ一通りに因数分解されるが,代数体の代数的整数の場合,例えば,有理数体に\(\sqrt{-5}\)を添加して得られる代数体Q(\(\sqrt{-5}\))の代数的整数全体Z[\(\sqrt{-5}\)]={a+b\(\sqrt{-5}\)|a,bは整数}では,6=2×3=(1+\(\sqrt{-5}\))(1-\(\sqrt{-5}\))となり,因数分解は必ずしも一通りではない。そこで,E.E.クンマーは,“理想数”の概念を導入し,整数のかわりに,理想数を用いると,代数的整数の場合にも,素数の積による因数分解と並行した理論が展開できることを示した。その後,J.W.デデキントは,理想数を考えることが,次の2条件を満たす部分集合を考えることと同等であることを示し,それら部分集合を,理想数にちなみイデアルIdeal(理想)と名づけた。
考えている代数体に含まれる代数的整数全体をAで表すと,(1)a,bが部分集合Iの元ならば,aとbの差a-bもまたIの元になる。(2)aがIの元,xがAの元であれば,x・aもIの元である。
イデアルIとJとの積を,Iの元とJの元との積全体を含む最小のイデアルと定義する。また,Aの元a1,……,anを含むAの最小のイデアルを(a1,……,an)で表すことにする。このとき,前の例における6は,(2,1+\(\sqrt{-5}\)),(2,1-\(\sqrt{-5}\)),(3,1+\(\sqrt{-5}\)),(3,1-\(\sqrt{-5}\))という四つの(それ以上分解しない)イデアルの積に分解する。代数的整数を考える場合,このような意味での〈イデアルのイデアルの積による素因数分解〉が常に可能である。
一般の可換環Aにおいても,上の2条件を満たす部分集合Iを,Aのイデアルと呼ぶ。非可換の環にも同様の定義で,左イデアルを定義し,さらに,(2)のx・aをa・xにおきかえて,右イデアルを定義する。Iが左イデアルかつ右イデアルになるとき,IをAの両側イデアルという。
整数論や環論にとどまらず,体を係数とする多変数多項式の作る環のイデアルや,ある領域で定義された関数のなす環のイデアルなど,数学の多くの分野で,イデアルおよびイデアルの概念が,重要な役割を果たしている。
執筆者:西村 純一
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
イデアル
ideal
整数の全体 (整数環) と多項式の全体 (多項式環) は,整除に関して類似の性質をもつ。しかし多項式でも多元多項式になると,整数や1元多項式のようには取扱えない。整数 m の代りに,m の倍数の全体 (m) を問題にしても同じことなので,このようなものとしてイデアルを考える。多元多項式になると,(m) のような形以外のイデアルが考えられることになるので,それを用いる有効性が生じるのである。また,環以外の構造についても,それと同じ技法で考えたものをイデアルと呼ぶ。 (1) 環のイデアル 多項式や整数は可換環であるが,可換でない一般の環においては,左イデアルと右イデアルを別々に定義することができる。環 R の部分集合 J が次の性質をもつとき,この J を R の左イデアルという。
(a) 零元は J に属する。
(b) J の2要素 x ,y の和,差も J に含まれる。
(c) J の要素 x に R の要素 a を左から掛けた ax も J に含まれる。
R 自身および零元もそれぞれイデアルである。同様に右イデアルは,上の (c) を x∈J ,a∈R ならば,xa∈J と修正した,加群としての R の部分群であると定義され,両側イデアルは,同じ条件のもとで,ax ,xa∈J がともに成り立つような,R の加法的部分群として定義できる。 (2) ブール代数のイデアル ブール代数 L の部分集合 J が次の条件を満足するとき,J は L が対応するブール環の構造に関してイデアルとなる。
(a) J の2要素の結びも J に含まれる。
(b) J の要素と L の要素との交わりが J に含まれる。
一般には,束 L の空でない部分集合 J が,上の条件を満足すれば,この J はイデアルと呼ばれる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のイデアルの言及
【環】より
…可換環A上のn次正方行列αが,可逆元であるための必要十分条件は,αの行列式がAの可逆元であることで,αの逆元をαの逆行列という。(4)イデアル 環Aの部分集合Iで,左A‐加群として,Aの部分加群であるものを,左イデアルという。同様に,右A‐加群を考え,右イデアルを定義する。…
【代数体の整数論】より
…代数体の整数論は,C.F.ガウスが4乗剰余の研究の中でガウス数体と呼ばれる体Q(i)(iは虚数単位)における整数論を考えたことに始まる。その後,E.E.クンマーによる円分体の研究や,J.W.デデキントによるイデアルの理論などによって形が整えられ,D.ヒルベルトの報文《Zahlbericht》においてその基礎が確立した。またヒルベルトが提出した[類体論]の構想は,その後の代数体の発展に重要な役割を果たした。…
【二次体の整数論】より
…この理論の大部分は,二次体の整数論として述べることができ,ここにおいて二次体の整数論の重要な部分が確立された。その後,P.G.L.ディリクレの解析的方法の応用や,J.W.R.デデキントのイデアルの理論などで,ガウスの理論がさらに進展し,二次体の整数論ができてきた。 以下,二次体の整数論の基本的事項について述べる。…
※「イデアル」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
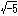 のような複素数の全体をZ[
のような複素数の全体をZ[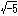 ]と表すと、Z[
]と表すと、Z[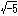 ]は可換環である。このZ[
]は可換環である。このZ[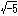 ]の要素のうちで、とくに整数x、yを用いて2x+(-1+
]の要素のうちで、とくに整数x、yを用いて2x+(-1+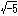 )yと表されるものの全体を[2,-1+
)yと表されるものの全体を[2,-1+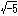 ]と表すと、この集合[2,-1+
]と表すと、この集合[2,-1+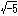 ]は単項イデアルでないことが示される。
]は単項イデアルでないことが示される。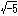 ]においては同じような展開をすることができない。そこでデーデキントは、整数にかわるものとしてイデアルという対象をとらえ、整数の理論の拡張としてイデアルの理論を建設したのである。
]においては同じような展開をすることができない。そこでデーデキントは、整数にかわるものとしてイデアルという対象をとらえ、整数の理論の拡張としてイデアルの理論を建設したのである。
