精選版 日本国語大辞典 「コンプトン効果」の意味・読み・例文・類語
コンプトン‐こうか‥カウクヮ【コンプトン効果】
- 〘 名詞 〙 物質によるX線の散乱において、散乱X線の波長が入射X線の波長より長くなる現象。一九二三年、コンプトンが発見。X線(光)の粒子性を立証する現象として重要で、アインシュタインの光量子説の正しさを決定づけた。
改訂新版 世界大百科事典 「コンプトン効果」の意味・わかりやすい解説
コンプトン効果 (コンプトンこうか)
Compton effect
X線が自由電子に当たって進路を曲げられる(散乱される。X線散乱という)とき,曲り角(散乱角)によって決まるわずかの値だけ波長が延びる現象。原子に束縛された電子でも,原子の外側にあるものについては束縛の影響はほとんど現れないので,同様にこの効果が観測される。1921年にA.H.コンプトンが実験により発見し,24年の末までには光が量子からなるという見方に対する最初の確固たる実験的証拠として受け入れられるようになった。それまで光量子(光子,フォトンともいう)は,A.アインシュタインが1905年に唱えた発見法的な見方としてのみ見られ,光電効果の精密実験も,X線の振動数と電子のエネルギーの関係を与えるアインシュタインの公式の証明として受け入れられこそすれ,物理学者の関心を光子に向けるにはいたらなかった。光の波動性との矛盾が乗り越えられなかったからである。コンプトンは,X線の波長の延びを,電子が光圧で押し動かされるために起こるドップラー効果として古典論で理解することはできないと指摘した。彼は,振動数νのX線はエネルギーがhνで運動量がhν/cの塊(光子)からなるというアインシュタインの見方に立ち,そのおのおのが一つの単位となってそれぞれ1個の電子に衝突すると考えた(hはプランク定数,cは光速)。その個々の衝突にエネルギーと運動量の保存則を適用することにより,X線の散乱角φと波長の延び⊿λとの実験値の関係を正しく再現する公式,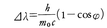 を得ることができたのである。ここにm0は電子の静止質量で,h/m0c=2.426×10⁻12mは電子のコンプトン波長と呼ばれる。散乱によってX線の波長が延びる(コンプトン散乱と呼ばれる)のは,そのときX線が電子をはねとばしてエネルギーhνの一部を失うため振動数νが減るからである。その減少は正面衝突でφ=180°となるとき最大だが,それでも波長の延びは2h/m0c≅5×10⁻12mにしかならないから,X線(λ≅10⁻8~10⁻13m)くらい波長の短い光でないと観測にかかりにくいわけである。
を得ることができたのである。ここにm0は電子の静止質量で,h/m0c=2.426×10⁻12mは電子のコンプトン波長と呼ばれる。散乱によってX線の波長が延びる(コンプトン散乱と呼ばれる)のは,そのときX線が電子をはねとばしてエネルギーhνの一部を失うため振動数νが減るからである。その減少は正面衝突でφ=180°となるとき最大だが,それでも波長の延びは2h/m0c≅5×10⁻12mにしかならないから,X線(λ≅10⁻8~10⁻13m)くらい波長の短い光でないと観測にかかりにくいわけである。
コンプトン効果は光の粒子性を鮮やかに浮き出させ,光の粒子性と波動性の矛盾を物理学者たちに避けて通れない問題としてつきつけることになった。光子の描像によればX線の波長の延びは計算できるが,しかし,X線の散乱角はどのくらいか(散乱角の頻度分布はどうなのか),散乱X線の強さはどうかという問いに理論的に答える役には立たない。これらの問いには,むしろX線の波動像に立つJ.J.トムソンの理論が(λ≫h/m0cなるかぎり)正しい答えをあたえる。J.C.スレーターは,光の粒子性を波動性と折り合わせるために,光子の道案内をし吸収や放出の確率をも決める場が存在すると考え,この場を通して原子たちは定常状態にある間も絶えず交信しているとした。N.ボーアとH.A.クラマースは,これを修正し,原子の不連続的な遷移は,その確率だけが誘導場の連続的な放出に伴って決められる統計現象だと主張した(1924)。そのため,エネルギーと運動量の保存則も個々の過程では必ずしも成立せず,単に統計的に成り立つにすぎないことになる。このボーア=クラマース=スレーターの説には,H.ガイガーとW.ボーテが直ちに反証をあげた。コンプトン効果における散乱X線と反跳電子は同時に発生しているように見え,これが偶然の一致である確率は10⁻5より小さいことを彼らは同時計数の方法で示したのである。さらにコンプトンとA.W.サイモンはコンプトン散乱の霧箱写真をとり,散乱角を測って個々の衝突でエネルギーと運動量の保存則が成り立っていることを直接に確かめた(1925)。これを否定する実験結果を1936年にR.S.シャンクランドが得て,一時はボーア=クラマース=スレーター理論の復活も取りざたされたが,50年にR.ホフスタッターらおよびN.F.ラムゼーらがそれぞれガイガー=ボーテ,コンプトン=サイモンの実験を精密化してこれに反証した。理論的にもエネルギー保存則が物理学の枠組みの中で根底的な地位を占め,容易には疑いえないものであることが論じられた。現在では光の粒子性と波動性は量子力学により矛盾なく統一的に記述される。コンプトン効果は,散乱X線の波長の延びも角度分布も強度も含めてあらゆる側面が量子電磁力学により計算できる。波長の延びはコンプトンの結果と一致し,散乱X線の角度分布と強度は反跳電子の同様の特性と合わせてクライン=仁科の公式に集約され,実験の及ぶかぎりの光の波長範囲でまちがいないことが確認されている。
執筆者:江沢 洋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「コンプトン効果」の意味・わかりやすい解説
コンプトン効果
こんぷとんこうか
Compton effect
電子によって散乱されたX線の波長が長波長側に変化する現象。コンプトン効果は、入射X線の波長や散乱体の種類によらない一方、散乱角度が大きいほど、また振動数の変化としては入射エネルギーが大きいほど、顕著に現れる。この効果は、1922年コンプトンによって物質によるX線の散乱でみいだされ、物質中の電子による光子の散乱として理解された。コンプトン効果は、光の粒子性(当時の光量子仮説)に対する直接的な実験的根拠を与えた。光子のエネルギーが、電子の静止エネルギーに比して十分小さいときの散乱は、トムソン散乱といわれ、散乱の度合い(全断面積)は入射エネルギーによらない。コンプトン効果は、光子と荷電粒子の間の相互作用による散乱過程であるから、電子に限らず陽子など他の荷電粒子の場合にも現れるが、効果は荷電粒子の質量が大きいほど小さいので、電子の場合がもっとも顕著に現れる。電磁場の量子である光子(フォトン)が振動数ν(エネルギーはνにプランク定数hを乗じた値)で静止している電子に入射し、角度θの方向に散乱されて振動数ν'になった場合、特殊相対性理論によるエネルギーと運動量の保存則を適用すると、ν'がνとθの関数として与えられ、ν'はνより小さい。振動数と波長の積が光速cとなる関係によって、波長がλよりλ'に増大する変化量は2λcsin2(θ/2)となる。ここで、λcは電子のコンプトン波長とよばれ、電子の質量をmとするとき
λc≒h/mc=2.4×10-12m
である。
[玉垣良三・植松恒夫]
『朝永振一郎著『量子力学1』第2版(1977・みすず書房)』▽『原康夫著『岩波基礎物理シリーズ5 量子力学』(1994・岩波書店)』
ブリタニカ国際大百科事典 小項目事典 「コンプトン効果」の意味・わかりやすい解説
コンプトン効果
コンプトンこうか
Compton effect
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
化学辞典 第2版 「コンプトン効果」の解説
コンプトン効果
コンプトンコウカ
Compton effect
光子の自由電子による非弾性散乱現象.1923年,A.H. Comptonにより発見された.光子のエネルギーをhν,運動量をhν/c(hはプランク定数,νは光子の振動数,cは光速度)とすると,光子と電子の衝突を図に示すような古典粒子間の衝突としてエネルギーおよび運動量の保存則を適用することができる.
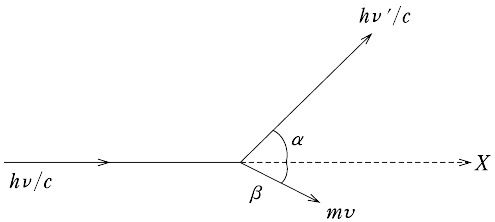
すなわち,エネルギー保存則より,次式が得られる.
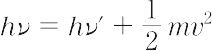
ここで,ν′は散乱光子の振動数,mは電子の質量,vはその反跳速度である.一方,運動量保存則により次の二式が成立する.
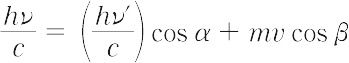
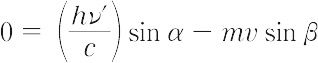
これらの三式から実験と一致する反跳電子の散乱方向に対するエネルギー分布などが計算できる.このように,光子を粒子として取り扱えることが示され,光の粒子性が確かめられた.ただし,上式において反跳電子が光速度に近くなるときは,相対論的取り扱いが必要になる.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
百科事典マイペディア 「コンプトン効果」の意味・わかりやすい解説
コンプトン効果【コンプトンこうか】
→関連項目X線|散乱|光|ボーテ
出典 株式会社平凡社百科事典マイペディアについて 情報
法則の辞典 「コンプトン効果」の解説
コンプトン効果【Compton effect】
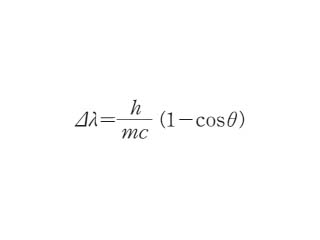
入射光子のエネルギーを Ep,散乱光子のエネルギーを Ep′ としたときには次のような式となる.
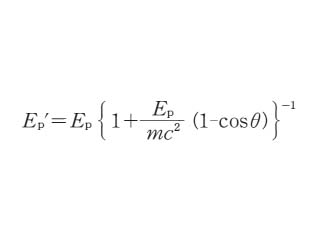
これとは別に高エネルギーの電子によって光子がエネルギーを得て短波長(高エネルギー)となって散乱される場合もあり,これは逆コンプトン効果*と呼ばれている.
世界大百科事典(旧版)内のコンプトン効果の言及
【X線】より
… 一方,X線の発見およびその研究は物理学の進歩に大きな波及効果を及ぼした。例えば,X線の発見に刺激を受けたA.H.ベクレルは,蛍光物質の中にはX線を放射するものがあるのではないかと考え,種々の物質を用いての実験を行ったが,1896年ウラン塩からX線とは異なる放射線が出ていることを発見しているし,また1922年,A.H.コンプトンによる散乱X線のコンプトン効果の発見は,電磁波(光)の粒子性の直接の証拠となったものとして有名である。
[基本的性質]
X線の最大の特徴は,物質を透過する力(透過能という)が大きく,物質に吸収されにくいことである。…
※「コンプトン効果」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...