フーリエ級数（読み）フーリエキュウスウ（英語表記）Fourier series

デジタル大辞泉

フーリエ‐きゅうすう〔‐キフスウ〕【フーリエ級数】

ある複雑な周期関数を、三角関数のような単純な周期関数の級数として表したもの。フランスの数学者フーリエによって導出。関数は区分的に連続かつ微分可能で滑らかであれば、級数は収束する。

出典　小学館

精選版 日本国語大辞典

フーリエ‐きゅうすう‥キフスウ【フーリエ級数】

1. 〘 名詞 〙 数学で、フランスの数学者フーリエの開発した級数のこと。関数を正弦関数と余弦関数で表現するのに用いる。〔電気工学ポケットブック（1928）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

フーリエ級数
ふーりえきゅうすう
Fourier series

区間［0,2π］で定義された周期2πの周期関数f(x)に対し、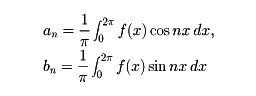

として、級数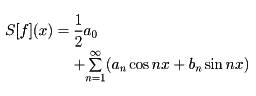

を考え、これを関数f(x)のフーリエ級数という。これはJ・フーリエが1810年代に熱拡散問題を解くために導入したものである。

　フーリエ級数で基本的な問題は、f(x)にどのような条件を置くと、級数S［f］(x)が収束し、その和がf(x)に等しくなるかである。この問題のむずかしさは、たとえばフーリエ級数S［f］(x)が各点でf(x)に収束するためには、f(x)が連続というだけでは十分でない（反例がある）。もうすこしf(x)に滑らかさを要求して、「周期関数f(x)が区分的に滑らかであるとは、区間［0,2π］において、有限個の点を除いてf´(x)が存在して有界連続となること」と定義すると、関数f(x)が［0,2π］において区分的に滑らかならば、f(x)のフーリエ級数S［f］(x)は任意の点xで1/2｛f(x-0)+f(x+0)｝に収束する。

　この結論は、f(x)が有界変動（f(x)=f₁(x)-f₂(x)と書けて、f₁(x),f₂(x)は単調増加関数）としてもそのまま成り立つ。

　このように関数f(x)を一般にする方向では、最終的な結果が、1966年にスウェーデンのL・カールソンによって得られた。それはf(x)が［0,2π］で自乗可積分、すなわち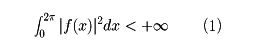

ならば、そのフーリエ級数S［f］(x)はほとんど至る所のxでf(x)に収束する。

［洲之内治男］

フーリエ級数のL²収束

［0,2π］で定義された自乗可積分（（1）を満足する）な関数の全体をL²［0,2π］で表し、f(x),g(x)∈L²［0,2π］に対して内積とノルムを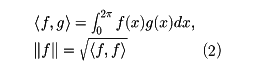

で定義すると、L²［0,2π］はヒルベルト空間になる。

　とくに関数列｛f_n(x)｝がf₀(x)に対し
　　‖f_n-f₀‖→0 (n→∞)
となるとき、｛f_n(x)｝はf₀(x)にL²収束（自乗平均収束）するという。このように収束の概念を拡張すると、周期2πをもつ連続関数f(x)に対し、そのフーリエ級数S［f］(x)はf(x)にL²収束することがいえる。

［洲之内治男］

直交関数系

一般に区間［a,b］上の自乗可積分な関数の全体をL²(a,b)とし、内積やノルムを、（2）をaからbまでの積分として定義すると、L²(a,b)はヒルベルト空間になる。｛_j(x)｝⊂L²(a,b)が〈_i,_j〉=0(i≠j)となるとき、｛_j(x)｝は直交関数系であるといい、さらに、すべてのjに対し、‖_j‖=1となっているとき正規直交関数系であるという。

　L²(a,b)の正規直交関数系｛_j(x)｝が与えられたとき、f(x)∈L²(a,b)に対し、c_j=〈f,_j〉としてつくった級数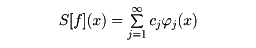

を｛_j(x)｝によるフーリエ級数という。正規直交系に関する展開はヒルベルト空間における一般論に含まれる。

　L²［0,2π］で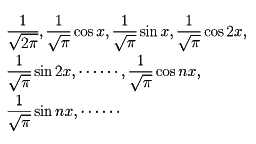

は正規直交関数系である。

　L²(-1,1)において、ルジャンドルの多項式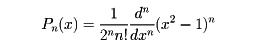

は直交関数系であり、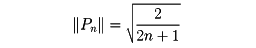

になる。

［洲之内治男］

『猪狩惺著『フーリエ級数』（1975・岩波書店）』

[参照項目] | 関数解析 | ヒルベルト空間

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

フーリエ級数 (フーリエきゅうすう)
Fourier series

区間（－π，π）において三角関数系，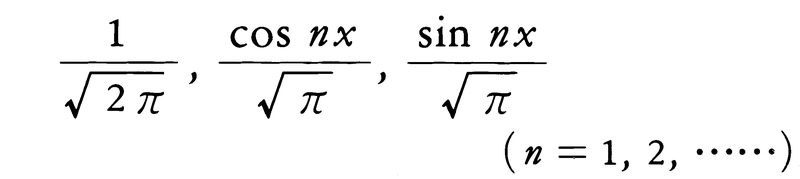

は正規直交系をなす。（－π，π）で積分可能な関数f（x）に対して，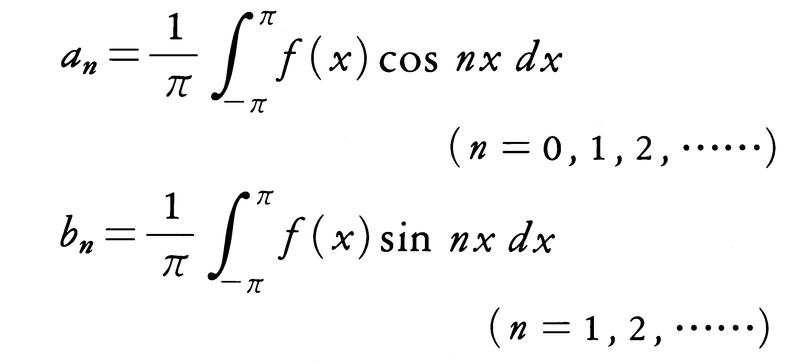

をf（x）のフーリエ係数といい，これを用いて作った級数，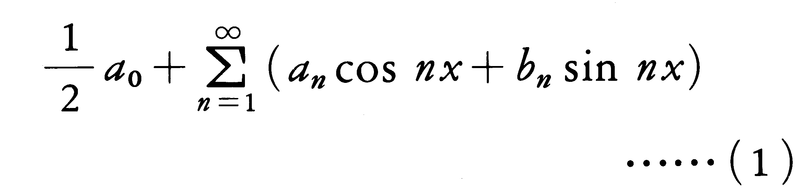

をf（x）のフーリエ級数という。指数関数系，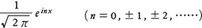

も（－π，π）において正規直交系をなすから，この関数系に関するフーリエ係数，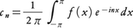

およびフーリエ級数，

を考える。f（x）が実数値関数ならば，c₀＝a₀，2c_n＝a_n－ib_n，c_-n＝c_n（n≧1）なる関係があり，（1）と（2）とは本質的に同じものと考えてよい。（1）を複素型のフーリエ級数と呼ぶこともある。フーリエ級数がどのような意味でもとのf（x）を表しているかが問題である。f（x）が（－π，π）で2乗可積分であれば，（1）で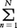とした部分和，または（2）で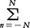とした部分和をs_n（x）とすると，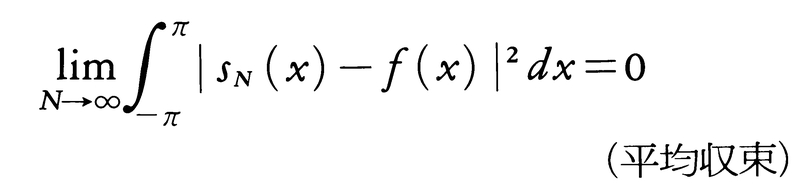

という意味でs_n（x）はf（x）に近づき，このときパーセバルの等式，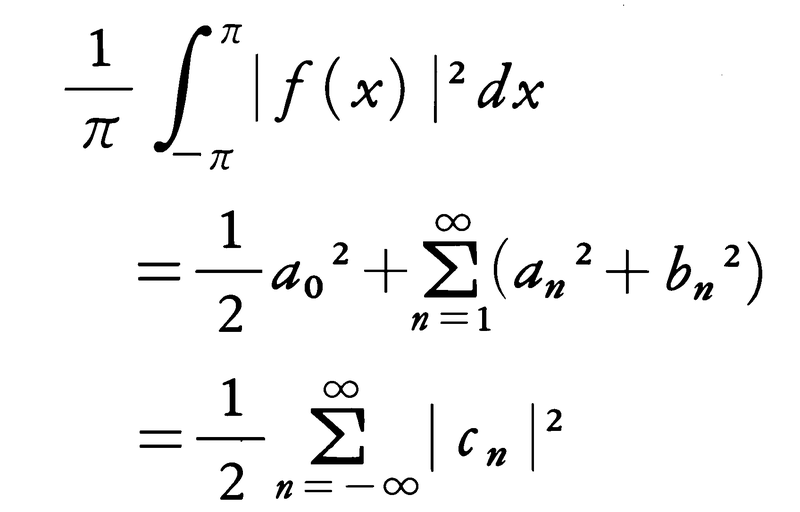

が成立する。f（x）が（－π，π）で有界変動ならば，そのフーリエ級数は，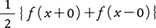

に収束する。さらにf（x）が連続ならば，そのフーリエ級数は任意の正数εに対して（－π＋ε，π－ε）で一様にf（x）に収束する。またf′（x）が有界ならば，そのフーリエ級数はf（x）に収束する。このほかにも種々の意味での収束性が調べられている。f（x）がフーリエ級数（1）で表されるとき，関数，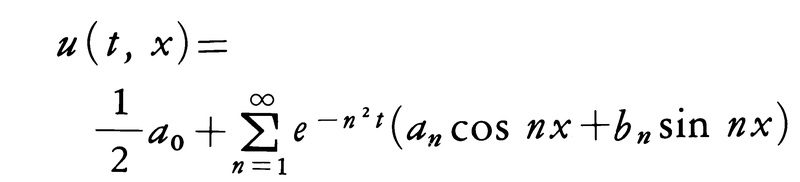

は熱伝導方程式∂u/∂t＝∂²u/∂x²と初期条件u（0，x）＝f（x）を満たす。J.B.J.フーリエが熱伝導論の研究においてこのような偏微分方程式を考察したのがフーリエ級数の起りである。
→直交関数系　→フーリエ解析
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

フーリエ級数
フーリエきゅうすう
Fourier series

J.フーリエが熱伝導の問題を扱っているときに導入した無限級数で，周期的な現象を研究するときに欠かせない。関数 f(x) を，区間 [a，b] で定義された1つの有界可積分関数とし，{ψ_n(x)} を [a，b] における正規直交関数列とする。もし，f(x) が f(x)＝c₁ψ₁(x)＋c₂ψ₂(x)＋… のように表わされるとき
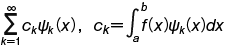で定義される級数を，{ψ_n(x)} に関する f(x) のフーリエ級数と呼び，次のように書く。
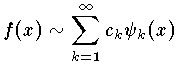ここに現れる数列 {c_n} を f(x) の {ψ_n(x)} に関するフーリエ係数という。 [a，b] として [－π，π] をとり，{ψ_n(x)} として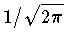， ， cos x/√π ， sin x/√π ，… ， cos nx/√π ， sin nx/√π とれば，f(x) のフーリエ級数は
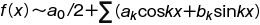の形となる。このような級数を三角級数と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

フーリエ級数【フーリエきゅうすう】

区間（−π，π）で定義された積分可能な関数f（x）に対し，（式１）を係数とする三角級数（式２）を，f（x）のフーリエ級数という。f（x）が適当な条件をみたすときf（x）のフーリエ級数は収束し，その和はf（x）に等しくなる。これはf（x）で表現される振動を振動数nの単振動に分解することに相当し，解析学や物理学の重要な手段となっている。→級数
→関連項目コルモゴロフ｜ディリクレ｜フーリエ｜ルベーグ

出典　株式会社平凡社

世界大百科事典（旧版）内のフーリエ級数の言及

【概周期関数】より

…a(λ)＝M_x[f(x)e^－iλx]とおくと，各f(x)に対してa(λ)≠0なるλはたかだか可算無限個しかない。それらをλ₁，λ₂，……，λ_n，……とし，a_n＝a(λ_n)とするとき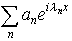，をfの(広義の)フーリエ級数という。これはふつうのフーリエ級数と類似の性質をもっている。…

【解析学】より

…前者の分野は複素関数論，または単に関数論と呼ばれ，後者は実関数論と呼ばれる。実関数論の方向は，J.フーリエの熱伝導に関する有名な論文(1812)に現れたいわゆるフーリエ級数に端を発するといえる。すなわち，P.ディリクレはフーリエ級数に関する二つの論文(1829,37)において，関数の現代的な定義を確立したが，その後リーマンが積分の一般的な定義を確立(1854)し，G.カントルが無理数論および集合論を創始した(1872)のも，フーリエ級数が誘因の一つであったと思われる。…

※「フーリエ級数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」