翻訳|vector
精選版 日本国語大辞典 「ベクトル」の意味・読み・例文・類語
ベクトル
改訂新版 世界大百科事典 「ベクトル」の意味・わかりやすい解説
ベクトル
vector
力を働かせて物を動かしてみると,同じ大きさの力でも,押すのと引くのではその効果はまったく違う。力は大きさだけでなく向きももつ。速度,加速度なども大きさと向きをもっている。このように大きさと向きをもった量のことをベクトルという。ベクトルは空間の向きをもった線分で表すことができる。線分の長さが大きさを表し,線分の向きがベクトルの向きを表す。線分の端点をP,Qとし,向きがPからQへ向かっているときQと記す。このとき,Pを始点,Qを終点という。力のベクトルの場合は始点を作用点とも呼ぶ。
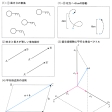
数学では,始点を固定して考えると不便な場合が多く,P,Q,P′,Q′が同じ平面の上にあり,線分とは平行で,かつを平行移動してPとP′を一致させ,QとQ′が一致するとき,Qと′とは同じベクトルを表すと考えるほうがつごうがよい。すなわち,Qと′の向き,方向,大きさが同じときは同じものと考えるのである(図1)。Qで表されるベクトルaの大きさは線分の長さと定め,これを|a|で示し,aの長さ,大きさ,絶対値などと呼ぶ。空間のかってな点Pを取ると,各ベクトルaについて点Qが存在して,aはQで表される。このときa=[Q]と書くことにする。a=[Q]と実数αとの積を,直線PQ上のPからみて,α≧0ならばQ側,α<0ならQと反対側の点Q′で,線分の長さが|α|となるものを取り,′が表すベクトルと定める。これをaのα倍といい,αaで表す。aの実数倍の形のベクトルをaのスカラー倍という。二つのベクトルa,bが与えられ,aをQ,bをRで表したとき,Rが定めるベクトルをaとbの和といい,a+bで表す。このa+bはPの取り方によらない。この和の定め方を平行四辺形の法則という(図2)。a+b=b+a,(a+b)+c=a+(b+c),実数α,βについて,α(a+b)=αa+αb,(α+β)a=αa+βaなどが成り立つ。′で表されるベクトルを零ベクトル(ゼロベクトル)という。零ベクトルを0で表せば,a+0=a,0a=0が成り立つ。
最初に述べた力のベクトルのように,始点が違うものは違うと考えるベクトルを束縛ベクトルといい,上記の平行移動で移りうるものは同じと考えるベクトルを自由ベクトルという。始点が同じ束縛ベクトルの和も平行四辺形の法則を使って定める。力のベクトルの場合,この和は力の合成にほかならない。
空間の直交座標系x,y,zを与えたとき,x軸上の正方向のPでの長さが1のものが表すベクトルiをx軸上の単位ベクトルという。同様に,y軸上,z軸上の単位ベクトルj,kが定まる。これらを座標単位ベクトルという。各ベクトルaはa=α1i+α2j+α3kと書けるが,この(α1,α2,α3)をaの座標成分という。aの長さは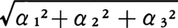 であり,αaの座標成分は(αα1,αα2,αα3)である。bの座標成分が(β1,β2,β3)ならば,a+bの座標成分は(α1+β1,α2+β2,α3+β3)である。
であり,αaの座標成分は(αα1,αα2,αα3)である。bの座標成分が(β1,β2,β3)ならば,a+bの座標成分は(α1+β1,α2+β2,α3+β3)である。
ベクトル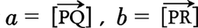 について,P,Q,Rが同一直線上にあれば,aとbは共線であるという。これは,ともには0でない実数α,βが存在して,αa+βb=0となることと同じである。
について,P,Q,Rが同一直線上にあれば,aとbは共線であるという。これは,ともには0でない実数α,βが存在して,αa+βb=0となることと同じである。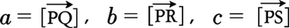 が共平面であるとは,P,Q,R,Sが同一平面上にあることである。共線のときと同様に,全部は0でない実数α,β,γがあって,αa+βb+γc=0となることと同値である。共平面でないベクトルa,b,cは一次独立であるという。a,b,cが一次独立であることと,[αa+βb+γc=0⇒α=β=γ=0]は同値である。例えば,座標単位ベクトルi,j,kは一次独立である。一次独立なベクトルa,b,cが与えられれば,かってなベクトルはαa+βb+γcと書ける。
が共平面であるとは,P,Q,R,Sが同一平面上にあることである。共線のときと同様に,全部は0でない実数α,β,γがあって,αa+βb+γc=0となることと同値である。共平面でないベクトルa,b,cは一次独立であるという。a,b,cが一次独立であることと,[αa+βb+γc=0⇒α=β=γ=0]は同値である。例えば,座標単位ベクトルi,j,kは一次独立である。一次独立なベクトルa,b,cが与えられれば,かってなベクトルはαa+βb+γcと書ける。
ベクトル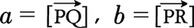 の内積を|a||b|cos(∠QPR)と定め,(a,b)またはa・bで表す。(a,b)=(b,a),(a+b,c)=(a,c)+(b,c),実数αについて,(αa,b)=α(a,b)が成立する。(a,b)=0となるとき,aとbは互いに直交するという。a,bの座標成分がそれぞれ(α1,α2,α3),(β1,β2,β3)ならば,(a,b)=α1β1+α2β2+α3β3である。
の内積を|a||b|cos(∠QPR)と定め,(a,b)またはa・bで表す。(a,b)=(b,a),(a+b,c)=(a,c)+(b,c),実数αについて,(αa,b)=α(a,b)が成立する。(a,b)=0となるとき,aとbは互いに直交するという。a,bの座標成分がそれぞれ(α1,α2,α3),(β1,β2,β3)ならば,(a,b)=α1β1+α2β2+α3β3である。
二つのベクトル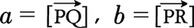 が定める平行四辺形の面積は,|a||b|sin(∠QPR)である。P,Q,Rが定める平面に垂直で,長さがこの面積であるベクトルをaとbのベクトル積といい,a×bで表す(図3)。ただし,a×bの向きは,aからbへ180度以内の角度でまわるとき,右ねじの進む方向と決める。a×b=-(b×a),(αa)×b=α(a×b),a×(b+c)=a×b+a×cが成り立つ。右手系の座標x,y,zを取り,座標単位ベクトルをi,j,kとすれば,a×b=(α2β3-α3β2)i+(α3β1-α1β3)j+(α1β2-α2β1)kとなる。ここで,(α1,α2,α3),(β1,β2,β3)はそれぞれa,bの座標成分である。
が定める平行四辺形の面積は,|a||b|sin(∠QPR)である。P,Q,Rが定める平面に垂直で,長さがこの面積であるベクトルをaとbのベクトル積といい,a×bで表す(図3)。ただし,a×bの向きは,aからbへ180度以内の角度でまわるとき,右ねじの進む方向と決める。a×b=-(b×a),(αa)×b=α(a×b),a×(b+c)=a×b+a×cが成り立つ。右手系の座標x,y,zを取り,座標単位ベクトルをi,j,kとすれば,a×b=(α2β3-α3β2)i+(α3β1-α1β3)j+(α1β2-α2β1)kとなる。ここで,(α1,α2,α3),(β1,β2,β3)はそれぞれa,bの座標成分である。
n次元ユークリッド空間の有向線分をベクトルと定めれば,空間のベクトルについて上に述べたことと同様のことがベクトル積を除いて考えられる。ベクトル積は三次元固有のものである。ベクトルの性質を抽象化して得られるものが線形空間であり,線形空間の性質を調べるのが線形代数学である。
→線形代数学
執筆者:丸山 正樹
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「ベクトル」の意味・わかりやすい解説
ベクトル
べくとる
vector
大きさだけでなく、方向と向きをもつ量。変位、力、速度、電場、磁場などはその例で、物理学で扱う量のなかには、このほかにもベクトルとして示される量は少なくない。これに対して、長さ、時間、質量、熱量などのように単位と数値だけで決まる量をスカラー(量)という。
たとえば、次のように平面上の二つの場合を考えてみる。〔1〕至る所で風力3の東風が吹いている。〔2〕どこからでもよいからある人が北方4キロメートル離れた地点まで移動する(の(1))。この二つの場合では、ともに方向と大きさという二つの要素だけで内容を完全に述べることができる。このように平面上で方向と大きさで規定される量を平面ベクトルという。平面を空間に置き換えれば、空間ベクトルが定義できる。以下記述を簡単にするために、平面ベクトルを単にベクトルとよび、これについて述べるが、空間ベクトルに対してもとくに補足がない限り同様である。
[高木亮一]
ベクトルを表す記号
ベクトルを表す記号としてはa, b, c,……とか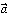 ,
,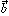 ,
,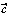 ,……とかを用いることが多い。ベクトルは次のように有向線分を用いて具体的に図示することができる(の(2))。平面上の任意の2点A、Bに対し、AからBに向かう矢印を有向線分といい、
,……とかを用いることが多い。ベクトルは次のように有向線分を用いて具体的に図示することができる(の(2))。平面上の任意の2点A、Bに対し、AからBに向かう矢印を有向線分といい、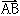 ,と書く。Aを始点、Bを終点という。これは方向と大きさ
,と書く。Aを始点、Bを終点という。これは方向と大きさ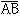 をもっているから、一つのベクトルaを表している。ところが、ベクトルは方向と大きさだけをもつ量であり、いいかえれば、同じ方向と同じ大きさをもつ二つのベクトルは同一であるから、向きと長さが等しい二つの有向線分はすべて同一のベクトルaを表していることになる。そのうちの任意の一つ
をもっているから、一つのベクトルaを表している。ところが、ベクトルは方向と大きさだけをもつ量であり、いいかえれば、同じ方向と同じ大きさをもつ二つのベクトルは同一であるから、向きと長さが等しい二つの有向線分はすべて同一のベクトルaを表していることになる。そのうちの任意の一つ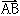 がベクトルaを代表しているとみなして、a=
がベクトルaを代表しているとみなして、a=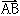 と書き表す。このように一つのベクトルを表す有向線分はたくさんあるが、そのうち、与えられた点を始点とするものはただ一つである。とくにA=Bのときも、
と書き表す。このように一つのベクトルを表す有向線分はたくさんあるが、そのうち、与えられた点を始点とするものはただ一つである。とくにA=Bのときも、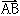 を有向線分と考えて、これが表すベクトルをゼロベクトルといい、0と書く。また線分ABの長さをaの大きさ、または長さ、または絶対値といい、|a|と書く。
を有向線分と考えて、これが表すベクトルをゼロベクトルといい、0と書く。また線分ABの長さをaの大きさ、または長さ、または絶対値といい、|a|と書く。
[高木亮一]
ベクトルとベクトルの和と差、ベクトルと実数との積
二つのベクトルa、bに対して、の(3)のようにa=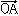 ,b=
,b=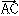 と表すとき、有向線分
と表すとき、有向線分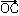 の表すベクトルcをaとbの和ベクトルまたは合成ベクトルといい、c=a+bと書く。これは、b=
の表すベクトルcをaとbの和ベクトルまたは合成ベクトルといい、c=a+bと書く。これは、b=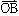 とも表すとき、OCが平行四辺形OACBの対角線になっていることを意味している(平行四辺形の法則)。
とも表すとき、OCが平行四辺形OACBの対角線になっていることを意味している(平行四辺形の法則)。
ベクトルaと実数λに対して、λが正またはゼロのときはaと同方向を、そして負のときはaと逆方向をもち、大きさがaの大きさの|λ|倍であるようなベクトルをaのスカラー倍といい、λaと書く。aと向きが逆でaと同じ大きさをもつベクトルをaの逆ベクトルといい、-aと書く。ベクトルa、b、cについては次の関係が成り立つ。
(1) a+b=b+a
(2) (a+b)+c=a+(b+c)
(3) a+0=a
(4) a+(-a)=0
(5) k(a+b)=ka+kb
(kはスカラー)
(6) k(la)=(kl)a
(k,lはスカラー)
(7) 1a=a
一つのベクトルaに対して、aおよびこれを表す有向線分の始点を組みにして考えたものを束縛ベクトルという。物理学で、力のベクトルとそれが作用する点を同時に考えるのはその例である。これと区別するために普通のベクトルa自身を自由ベクトルという。平面に原点Oを定めると、平面の任意の点Aに対して、有向線分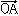 の表すベクトルが定まるが、これをAの位置ベクトルという。このようにして、点Oを定めると、平面の点と位置ベクトルが一対一に対応するので、この意味において平面をベクトルの集合とみなすのが普通である。なお、大きさが一のベクトルを単位ベクトルという。
の表すベクトルが定まるが、これをAの位置ベクトルという。このようにして、点Oを定めると、平面の点と位置ベクトルが一対一に対応するので、この意味において平面をベクトルの集合とみなすのが普通である。なお、大きさが一のベクトルを単位ベクトルという。
二つのベクトルe1、e2のどちらも他方のスカラー倍になっていないとき、これらを基本ベクトルという(空間においては、ベクトルe1、e2、e3が同一の平面に含まれる3本の有向線分によって表されないとき、これらを基本ベクトルという)。たとえば、直交座標軸に平行な二つの(空間では三つの)単位ベクトルは基本ベクトルである(の(4))。e1、e2(空間ではe1、e2、e3となるが、以下空間については省略する)が基本ベクトルのとき、任意のベクトルaはただ1通りの方法で
a=a1e1+a2e2
と表すことができる。(a1,a2)をe1、e2に関する成分という。このように、基本ベクトルを一つ定めておけばベクトルaをその成分(a1,a2)で表示できるので、a=(a1,a2)とも書く。この表示法でベクトルの和とスカラー倍を書くと、簡単に、
(a1,a2)+(b1,b2)
=(a1+b1,a2+b2)
k(a1,a2)=(ka1,ka2)
となる。
[高木亮一]
ブリタニカ国際大百科事典 小項目事典 「ベクトル」の意味・わかりやすい解説
ベクトル
vector
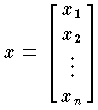 のように,n 個の成分をもった n 次元の量ということになる。これは,(x1,x2,…,xn) のように横に書く流儀もあるが,V 上の1次形式は
のように,n 個の成分をもった n 次元の量ということになる。これは,(x1,x2,…,xn) のように横に書く流儀もあるが,V 上の1次形式は 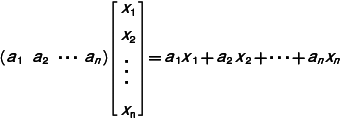 のように書けるので,行列算の立場から,横ベクトルは1次形式の全体 V* の元として区別する流儀もある。内積の考えられるときは,0 でないベクトルは
のように書けるので,行列算の立場から,横ベクトルは1次形式の全体 V* の元として区別する流儀もある。内積の考えられるときは,0 でないベクトルは 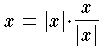 と,極座標のように,大きさ |x| と方向 x/|x| に分解できる。それで,方向と大きさをもった量として,ベクトルは有向線分で表示する。これに対して,係数体 K の元はスカラーという。さらに,3次元ユークリッド空間では,対称による効果も考えて,変換 x→-x で符号を考える普通の場合をベクトル,ベクトル積 x×y のように符号を変えない場合を擬ベクトルといって区別することもある。
と,極座標のように,大きさ |x| と方向 x/|x| に分解できる。それで,方向と大きさをもった量として,ベクトルは有向線分で表示する。これに対して,係数体 K の元はスカラーという。さらに,3次元ユークリッド空間では,対称による効果も考えて,変換 x→-x で符号を考える普通の場合をベクトル,ベクトル積 x×y のように符号を変えない場合を擬ベクトルといって区別することもある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「ベクトル」の意味・わかりやすい解説
ベクトル
→関連項目加速度|スカラー
出典 株式会社平凡社百科事典マイペディアについて 情報
日本の企業がわかる事典2014-2015 「ベクトル」の解説
ベクトル
栄養・生化学辞典 「ベクトル」の解説
ベクトル
世界大百科事典(旧版)内のベクトルの言及
【スピノル】より
…電子のように1/2のスピンをもつ状態,さらに一般に任意のスピンをもつ状態を表すために導入された量で,スピノルの名もスピンに由来している。三次元空間を回転させたとき,その中の量は回転に伴って変化するが,その変化のしかたによってスカラー,ベクトル,テンソルなどに区別される。変化しないものをスカラーといい,空間内の変位を表す矢印と同じようにふるまうのがベクトルであり,数個のベクトルの積と同じように変化するのが高階のテンソルである。…
【力】より
… 物理学での力forceの定義は普通ニュートンの運動方程式を用いて次のようになされる。すなわち力というのは平行四辺形の合成則にしたがうベクトル量であって,物体の運動量p=mv(mは物体の(慣性)質量,vは速度)を変化させる働きをもつ。このとき,小さな時間⊿tの間にpに⊿pだけの変化を生ずるとすると,pの瞬間的変化率,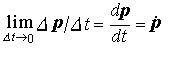 と,働いている力Fの間に,
と,働いている力Fの間に,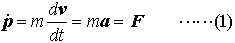 という関係(ニュートンの運動方程式)がある。…
という関係(ニュートンの運動方程式)がある。…
※「ベクトル」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...